Primitieven

Inleiding

Isaac Newton ontdekte al dat je integralen exact kunt berekenen door gebruik te maken van "omgekeerd differentiëren". Later werd de hoofdstelling van de integraalrekening bewezen: je kunt de integraal van f op [a,b] berekenen vanuit het functievoorschrift f(x) door daarbij een functievoorschrift F(x) te zoeken zo, dat F'(x) = f(x) en dan
F(b) – F(a) uit te rekenen. Deze functie F noem je een primitieve van f.
Dit gaan we nu aannemelijk maken en toepassen...

Je leert nu:

• de integraal van een functie berekenen door primitiveren;
• het begrip primitieve van een functie;
• in eenvoudige gevallen primitieven van functies bepalen.

Je kunt al:

• functies differentiëren;
• integralen bepalen met behulp van je grafische rekenmachine.

Verkennen

De primitieve functie F van een functie f met voorschrift f(x) heeft een functievoorschrift F(x) zo, dat F'(x) = f(x).
Je kunt zo'n primitieve vinden door "omgekeerd te differentiëren".
Daarna controleer je door differentiëren of hij goed is.

> Laat zien dat F(x) = $\frac{1}{3}$x³ een primitieve is van de functie f(x) = x².
> Laat zien dat elke functie F(x) = $\frac{1}{3}$x³ + c een primitieve is van de functie f(x) = x².
> Welke functies zijn primitieven van f(x) = x⁵?
> >Welke functies zijn primitieven van f(x) = 0,5x⁴ – 4x?

Uitleg

Je ziet hier de grafiek van de functie f met f(t) = 0,5t².
Op [1,x] is de integraal van f gelijk aan ${\displaystyle \underset{1}{\overset{x}{\int }}\mathrm{0,5}{t}^2\text{d}t}$.
Deze integraal is een functie van x: F(x).
Laat je x een heel klein beetje toenemen naar x + h, dan neemt F(x) toe met: F(x + h) – F(x) ≈ f(x) · h.
Hieruit volgt: $\frac{F(x+h)-F(x)}{h}$ ≈ f(x).
Laat je vervolgens h naar nul naderen, dan vind je:
$\underset{h\to 0}{\lim }\frac{F(x+h)-F(x)}{h}$ = f(x) en dus F'(x) = f(x).

Je moet kennelijk de integraal F(x) vinden vanuit zijn afgeleide f(x) = 0,5x². Dit betekent: terugrekenen vanuit een afgeleide. Dat noem je primitiveren en de functie die je vindt heet een primitieve functie van f. Ga na, dat: F(x) = $\frac{1}{6}$x³ + c voldoet.
Hierin is c een willekeurige constante. Een functie heeft namelijk niet één primitieve, maar een hele verzameling: een constante bijtellen verandert de afgeleide niet!
Maar omdat hier geldt F(1) = 0 moet c = –$\frac{1}{6}$, dus ${\displaystyle \underset{1}{\overset{x}{\int }}\mathrm{0,5}{t}^2\text{d}t}$ = $\frac{1}{6}$x³ – $\frac{1}{6}$ = F(x) – F(1).
Kies een waarde voor x en je kunt de integraal berekenen.

‡

Opgaven

1. In de Uitleg wordt verteld hoe je een integraal exact kunt berekenen door primitiveren.
   1. Wat is primitiveren precies?
   2. Leg uit waarom `F(x) = 1/6 x^3` een primitieve is van `f(x) = 0,5x^2`.
   3. Noem nog minstens twee andere primitieve functies van `f`.
   4. Waarom is `int_(1)^(x) 0,5x^2 text(d)x = F(x) - F(1)`?
   5. Bereken nu `int_(1)^(4) 0,5x^2 text(d)x`.
   6. Bereken ook `int_(2)^(4) 0,5x^2 text(d)x`.


2. Gegeven is de functie `f` met `f(x) = 15x^4`.
   1. Wat stelt `F(x) = int_(-1)^(x) f(t) text(d)t` voor?
   2. Toon aan dat `F'(x) = f(x)`.
   3. Bepaal nu zelf de juiste primitieve functie `F` van `f`.
   4. Wat stelt `F(2)` voor? Bereken `F(2)`.

Theorie

Integralen kun je in veel gevallen exact berekenen.
Daarbij maak je gebruik van de stelling:
${\displaystyle \underset{a}{\overset{x}{\int }}f(t)\text{d}t}$ = F(x) – F(a) waarin F een functie is waarvoor geldt: F'(x) = f(x).

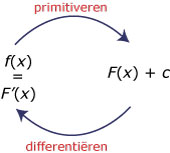
Je vindt F(x) vanuit zijn afgeleide f(x). Dit betekent: terugrekenen vanuit een afgeleide. Dat noem je primitiveren en de functie die je vindt heet een primitieve functie van f.

Het vinden van primitieve functies is vaak nog niet zo eenvoudig.
Met behulp van differentiëren kun je laten zien:

• Als f(x) = x^r dan is F(x) = $\frac{1}{r+1}$ x^r + 1 + c voor elke reële waarde r ≠ –1.
• De primitieve functies van k · f(x) zijn k · F(x) + c.
• De primitieve functies van f(kx) zijn $\frac{1}{k}$ · F(kx) + c
• De primitieve functies van f(x + k) zijn F(x + k) + c
• De primitieve functies van f(x) + k zijn F(x) + kx + c
• De primitieve functies van f(x) + g(x) zijn F(x) + G(x) + c

Hierin is telkens c de integratieconstante. Elke functie f heeft oneindig veel primitieven die alleen een constante verschillen.

‡

Voorbeeld 1

Hier zie je een aantal primitieven van functies.

• f(x) = x⁴ dus F(x) = $\frac{1}{5}$x⁵ + c

• f(x) = 3x⁴ dus F(x) = 3 · $\frac{1}{5}$x⁵ + c = $\frac{3}{5}$x⁵ + c

• f(x) = 0,5x⁴ – 4x² + 2
  dus F(x) = 0,5 · $\frac{1}{5}$x⁵ – 4 · $\frac{1}{3}$x³ + 2x + c = 0,1x⁵ – $\frac{4}{3}$x³ + 2x + c

• f(x) = (3x + 1)⁵ dus F(x) = $\frac{1}{6}$(3x + 1)⁶ · $\frac{1}{3}$ + c = $\frac{1}{18}$(3x + 1)⁶ + c

• f(x) = $\frac{2}{5x^3}$ = $\frac{2}{5}$x^–3 dus F(x) = –$\frac{1}{5}$x^–2 + c = $\frac{-1}{5x^2}$ + c

• f(x) = $3x\sqrt{2x}$ = 3$\sqrt{2}$x^1,5 dus F(x) = 3$\sqrt{2}$ · $\frac{1}{\mathrm{2,5}}$x^2,5 + c = 1,2x²$\sqrt{2x}$ + c

‡

Voorbeeld 2

Gegeven is de functie f door f(x) = $\frac{x^4-16}{2x^2}$.
Deze functie heeft een primitieve waarvan de grafiek door het punt P(1,5) gaat.
Stel het functievoorschrift van die primitieve op.

Antwoord

Door uitdelen vind je: f(x) = $\frac{1}{2}$x² – 8x^–2.
Dus is F(x) = $\frac{1}{2}$ · $\frac{1}{3}$x³ – 8 · $\frac{1}{-1}$x^–1 + c = $\frac{1}{6}$x³ + $\frac{8}{x}$ + c

Dit is een hele verzameling primitieven. Je zoekt de primitieve die door P(1,5) gaat. Voor die primitieve moet dus gelden F(1) = 5. Dit betekent:
$\frac{1}{6}$ + 8 + c = 5 en dus c = –3$\frac{1}{6}$.
De gevraagde primitieve is F(x) = $\frac{1}{6}$x³ + $\frac{8}{x}$ – 3$\frac{1}{6}$.

‡

Voorbeeld 3

Gegeven is de functie f door f(x) = $\frac{(x-2)(x-9)}{\sqrt{x}}$.
V is het vlakdeel ingesloten door de grafiek van f en de x-as.
Bereken de oppervlakte van dit vlakdeel met behulp van primitiveren in twee decimalen nauwkeurig.

Antwoord

Eerst de functie herschrijven: f(x) = $\frac{x^2-11x+18}{x^{\mathrm{0,5}}}$ = x^1,5 – 11x^0,5 + 18x^–0,5.
De primitieve van f is:
F(x) = $\frac{1}{\mathrm{2,5}}$x^2,5 – $\frac{11}{\mathrm{1,5}}$x^1,5 + $\frac{18}{\mathrm{0,5}}$x^0,5 + c = $\frac{2}{5}$x²$\sqrt{x}$ – $\frac{22}{3}$x$\sqrt{x}$ + 36$\sqrt{x}$ + c.

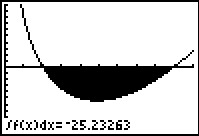
Kijkend naar de grafiek van f constateer je dat het gaat om de integraal van f op het interval [2,9]. Alleen zijn dan alle functiewaarden negatief en daarom de uitkomst ook.
De gevraagde oppervlakte is ${\displaystyle \underset{2}{\overset{9}{\int }}-f(x)\text{d}x}$ = –F(9) – –F(2) ≈ 25,23.

‡

Opgaven

3. Bekijk in de Theorie wat je onder een primitieve verstaat en welke regels je kunt toepassen om ze te bepalen.
   1. Controleer de juistheid van elke regel door differentiëren.
   2. In Voorbeeld 1 worden verschillende primitieven bepaald. Probeer steeds eerst zelf de primitieve te vinden.
   3. Controleer alle primitieven door differentiëren.


4. Gegeven is de functie `f(x) = sqrt(x)` op het interval `[0,5]`.
   1. Wat stelt `F(x) = int_(0)^(x) f(t) text(d)t` voor?
   2. Waarom is `F` een primitieve van `f`?
   3. Bepaal alle mogelijke functies `F` met behulp van de machtsregel voor primitiveren.
   4. Bereken nu exact `int_(0)^(9) sqrt(x) text(d)x`.


5. Het berekenen van de primitieven van een functie wordt ook wel onbepaald integreren genoemd. Je noteert dit met een integraalteken zonder grenzen. Bepaal:
   1. `int 3x^2 - 4x + 1 text(d)x`
   2. `int root[3](x) text(d)x`
   3. `int 2/(x^2) text(d)x`
   4. `int sqrt(3x) text(d)x`
   5. `int (4x - 1)^2 text(d)x`
   6. `int (x^2 - 4)/(x^2) text(d)x`


6. In Voorbeeld 2 wordt een primitieve berekend die aan een bepaalde randvoorwaarde voldoet.
   1. Bereken de primitieve `F` van `f(x) = 1/(x^2) + x^2` waarvoor geldt `F(1) = 2`.
   2. Bereken de primitieve `F` van `f(x) = (3x - 4)/(x^3)` waarvoor geldt `F(1) = 2`.
   3. Bereken de primitieve `F` van `f(x) = (4x - 2)^3` waarvoor geldt `F(0) = 1`.
   4. Bereken de primitieve `F` van `f(x) = 1/(sqrt(1 + 4x))` waarvoor geldt `F(2) = 0`.


7. Bestudeer nu Voorbeeld 3.
   1. Ga na dat de primitieven `F` van de gegeven functie `f` juist zijn.
   2. Je moet nu `int_(2)^(9) -f(x) text(d)x` berekenen. Bepaal de functie `G` waarvoor `G(x) = -F(x)` waarvoor geldt `G(2) = 0`.
   3. Bereken met behulp van het antwoord van b de gewenste integraal.
   4. Controleer je antwoord met de grafische rekenmachine.


8. Gegeven is de functie `f(x) = 4 - x^2` op het interval `[-4,4]`.
   1. Bepaal de primitieve `F` van `f` waarvoor geldt `F(-4) = 0`.
   2. Bereken met behulp van de primitieve die je bij a hebt gevonden de integraal van `f` op het gegeven interval.
   3. Is deze integraal gelijk aan de oppervlakte van de gebieden ingesloten door de grafiek van `f`, de `x`-as en de lijnen `x = -4` en `x = 4`? Licht je antwoord toe.

Verwerken

9. Voor `x >= 0` is gegeven de functie `F(x) = int_(0)^(x) t^3 - 8t text(d)t`.
   1. Welke betekenis heeft de functiewaarde `F(2)`? Bereken `F(2)` exact.
   2. Bereken de extremen van `F`.
   3. Voor welke `x` geldt `F"(x) = 0`?
   4. Stel een vergelijking op van de raaklijn aan de grafiek van `F` voor die waarde van `x`.


10. Bereken de primitieven van `f`.
    1. `f(x) = (3x - 2)^4`
    2. `f(x) = x(1 + x^2)`
    3. `f(x) = (1 + x^2)^2`
    4. `f(x) = 4/(2x + 1)^2`


11. Bekijk de voorgaande opgave. Bepaal in elk van de gevallen de primitieve functie `F` waarvoor `F(0) = 1`.
    


12. Bereken de volgende onbepaalde integralen:
    1. `int 1/(sqrt(x)) text(d)x`
    2. `int (3x - 2)^11 text(d)x`
    3. `int (x^2 sqrt(x) + 4 sqrt(x)) text(d)x`
    4. `int 3(3x + 5)^4 text(d)x`


13. Gegeven is de functie `f` met `f(x) = 6x - 3x^2`.
    Je wilt de oppervlakte uitrekenen van het gebied ingesloten door de grafiek van `f` en de `x`-as.
    1. Om welke integraal gaat het dan?
    2. `F(x) = int_(0)^(x) f(t) text(d)t`. Stel een voorschrift op voor `F`.
    3. Bereken met behulp van `F` de gewenste oppervlakte.
    4. Controleer je antwoord met de grafische rekenmachine.

Testen

14. Gegeven is de functie `f` met `f(x) = sqrt(4 - x)`.
    Je wilt de oppervlakte uitrekenen van het gebied ingesloten door de grafiek van `f`, de `x`-as en de `y`-as.
    1. Om welke integraal gaat het dan?
    2. `F(x) = int_(0)^(x) f(t) text(d)t`. Stel een voorschrift op voor `F`.
    3. Bereken met behulp van `F` de gewenste oppervlakte.
    4. Controleer je antwoord met de grafische rekenmachine.


15. Bepaal de primitieve `F` van de functie `f` waarvoor `F(0) = 1` als
    1. `f(x) = sqrt(2x) + 1/(sqrt(2x))`
    2. `f(x) = 3/((3x + 4)^2)`