
De integraal

Inleiding
Een waterleidingmaatschappij zorgt voor veilig drinkwater. Ze slaan dit op in grote spaarbekkens. Er stroomt vrijwel voortdurend water in en ook wordt er voortdurend water aan onttrokken. Het verschil tussen instroom en uitstroom is de stroom in m3/uur en afhankelijk van de tijd t in uren.
Je kunt van die stroom een grafiek maken en daarmee bepalen hoeveel water er aan het einde van een dag (ongeveer) in het spaarbekken is bijgekomen of afgegaan.
Je leert nu:
- de integraal van een functie bepalen;
- de begrippen ondersom en bovensom en Riemann-som;
- Riemann-sommen berekenen.
Je kunt al:
- werken met alle basisfuncties.
Verkennen
In een groot spaarbekken stroomt vrijwel voortdurend water in en ook wordt er voortdurend water aan onttrokken. Het verschil tussen instroom en uitstroom is de stroom in m3/uur en afhankelijk van de tijd t in uren.
Je kunt van die stroom een grafiek maken en daarmee bepalen hoeveel water er aan het einde van een dag (ongeveer) in het spaarbekken is bijgekomen of afgegaan.
Je kunt bijvoorbeeld elk uur een ondergrens en een bovengrens van de hoeveelheid stroom vaststellen. Positieve waarden betekenen dat er meer instroom dan uitstroom is, bij negatieve waarden is dat andersom. De bovensom is het totaal van de bovengrenzen per uur, de ondersom dat van de ondergrenzen per uur.
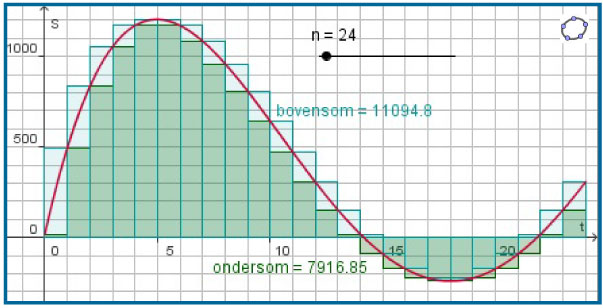
> Hoeveel schat je dat er die dag aan m3 water is bijgekomen?
> Hoe kun je de schatting verbeteren?
Uitleg
Bekijk de grafiek van het verschil tussen instroom en uitstroom van een spaarbekken nog eens. De hoeveelheid die deze dag erbij is gekomen ligt in tussen bovensom en ondersom.
Door de tijdseenheid Δt te verkleinen, kun je bovensom en ondersom nauwkeuriger vaststellen. Ze komen dan dichter bij elkaar te liggen en je schatting wordt beter. De ondersom is het totaal van Smin(t) · Δt waarin Smin steeds het minimum van S op elk deelinterval is. Zo is de bovensom het totaal van Smax(t) · Δt.
De integraal van S is nu het getal waar bovensom en ondersom beide naar naderen.
De integraal van S is het getal waar bovensom en ondersom beide naar naderen.
Dit veronderstelt wel dat ze inderdaad naar hetzelfde getal naderen, een belangrijke voorwaarde voor het bestaan van de integraal.
Verdeel je het interval [0,24] in n gelijke deelintervallen, dan is de ondersom is het totaal van Smin(t1) · Δt + Smin(t2) · Δt + ... + Smin(tn) · Δt.
Dit schrijf je korter als
En zo is bovensom in formulevorm
Als dan bestaat de integraal. Hij wordt aangeduid als
Ondersommen en bovensommen zijn met de grafische rekenmachine te bepalen.
De grafische rekenmachine kan echter ook rechtsreeks een integraal voor je benaderen.
In beide gevallen heb je dan een functievoorschrift voor S nodig.
‡
Opgaven
-
In de Uitleg wordt de toename en de afname per uur van de hoeveelheid water in een spaarbekken beschreven.
Er is een grafiek getekend die iets te maken heeft met de hoeveelheid water in het bekken.
- Wat stelt deze grafiek precies voor?
- Hoe kun je de totale hoeveelheid bijgekomen water aan het einde van deze dag berekenen?
- Voer die berekening uit op basis van intervallen van 1 uur.
- Voer die berekening nog eens uit op basis van intervallen van 0,5 uur.
-
De hoeveelheid water `H` in het spaarbekken op `t = 0` was `H(0) = 10000`. Je hebt nu
aan het eind van de voorgaande opgave een schatting gemaakt van `H(24) - H(0)`.
- Leg uit dat je hebt berekend: `H(24) - H(0)`.
- De grafiek is in drie delen te verdelen: twee delen waarbij stroom positief is en een deel waarbij stroom negatief is.
Welk verband bestaat er tussen deze schatting en de oppervlakte tussen deze drie delen van de grafiek en de `t`-as?
-
De variabele stroom wordt voorgesteld door de functie `f(t)`.
- Neem een tijdsinterval van 0,25 uur. Bereken de ondersom van `f(t)` op het interval `[0,24]`.
- Bereken vervolgens de bovensom van `f(t)` op ditzelfde interval.
- Welke waarde schat je nu voor de integraal van `f(t)` over dit interval?
- Wat stelt je antwoord bij c voor?
Theorie
Onder de integraal van een functie f op het interval [a,b] versta je de som van alle waarden van f(xk) · Δx op dit interval als Δx naar 0 nadert.
Zo'n integraal benader je zo:
- Verdeel het interval [a,b] in n (gelijke) deelintervallen met breedte Δx. Bij elk deelinterval maak je een rechthoek met breedte Δx en als hoogte de kleinste functiewaarde op dat deelinterval én een rechthoek met breedte Δx en als hoogte de grootste functiewaarde op dat deelinterval.
- De ondersom is fmin(x1) · Δx + fmin(x2) · Δx + ... + fmin(xn) · Δx, wat je kortweg schrijft als
- De bovensom is fmax(x1) · Δx + fmax(x2) · Δx + ... + fmax(xn) · Δx, wat je kortweg schrijft als
Als dan bestaat de integraal. Hij wordt aangeduid als
Het bepalen van Riemannsommen als ondersom en bovensom is een lastige bezigheid.
De grafische rekenmachine kan ook rechtstreeks de integraal voor je benaderen.
In beide gevallen heb je dan het functievoorschrift f(x) nodig.
‡
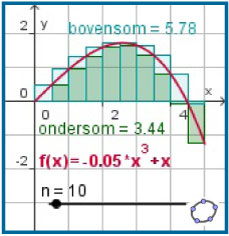
Voorbeeld 1
Je ziet hier de grafiek van de functie f met f(x) = –0,05x3 + x op het interval [0,5].
Benader met de grafische rekenmachine de bovensom en de ondersom die in de figuur zijn aangegeven.
Benader ook de integraal .
Antwoord
Met 5 deelintervallen van lengte 1 wordt de ondersom:
= 1 · f(0) + 1 · f(1) + 1 · f(2) + 1 · f(4) + 1 · f(5).
Voor de bovensom heb je op het derde deelinterval het maximum van f op dat interval nodig.
Met je GR vind je max.f(2,58) ≈ 1,72.
De bovensom wordt:
= 1 · f(1) + 1 · f(2) + 1 · f(2,58) + 1 · f(3) + 1 · f(4).
Ga zelf na, dat je de waarden uit de figuur vindt.
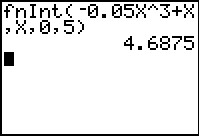
De integraal kun je gemakkelijk met je GR benaderen.
Uiteraard vind je een waarde tussen ondersom en bovensom in.
Als je n verhoogt gaan onder- en bovensom de integraal benaderen.
‡
Voorbeeld 2
Bekijk de grafiek van de functie f met f(x) = 0,5x2.
Omdat op [1,5] geldt dat f(x) ≥ 0, is de integraal de oppervlakte van het vlakdeel V ingesloten door de grafiek van f de x-as en de twee lijnen x = 1 en x = 5.
Bereken de oppervlakte van V in twee decimalen nauwkeurig.
Antwoord
Dit gaat rechtstreeks met de grafische rekenmachine.
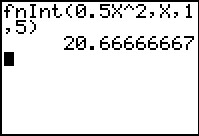 De oppervlakte van V is:
De oppervlakte van V is:
Opp(V) = ≈ 20,67.
‡
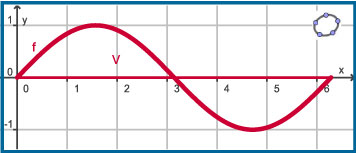
Voorbeeld 3
Je ziet hier de grafiek van de functie f met f(x) = sin(x) op [0,2π].
Bereken
en bereken de oppervlakte van het vlakdeel V ingesloten door de grafiek van f en de x-as.
Antwoord
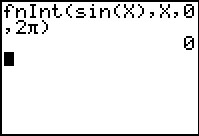
Met je GR vind je meteen: = 0.
Dat ligt ook voor de hand, want de standaard sinusfunctie heeft op [π,2π] dezelfde functiewaarden als op [0,π], alleen zijn ze op [π,2π] negatief en op [0,π] positief.
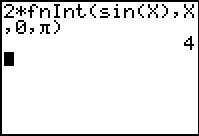
Wil je de gevraagde oppervlakte weten, dan moet je en optellen. Je kunt dan sneller 2 · berekenen.
Je ziet dat de gevraagde oppervlakte 4 is.
‡
Opgaven
-
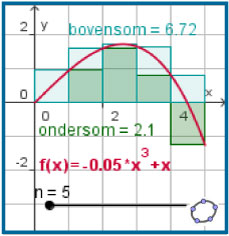
Bekijk in de Theorie wat de integraal van een functie over een bepaald interval voorstelt en bekijk in Voorbeeld 1 hoe je in een bepaald geval zo'n integraal benadert met behulp van Riemann-sommen.
- Controleer eerst of je ook inderdaad de in de figuur gegeven Riemann-sommen krijgt.
- Verdeel nu het gegeven interval in 10 gelijke deelintervallen. Bereken opnieuw de ondersom en de bovensom en geef een benadering van de integraal.
- Benader de integraal met je grafische rekenmachine, bestudeer eventueel eerst het practicum op de math4allsite.
-
Gegeven is de functie `f(x) = 2x` op het interval `[0,5]`.
- Teken de grafiek van de functie. Verdeel het interval `[0,5]` in vijf gelijke delen en bepaal de onder- en de bovensom.
- Geef een schatting van de integraal van `f` op het interval `[0,5]`.
- Verdeel het interval `[0,5]` in tien gelijke deelintervallen en bereken de onder- en bovensom. Geef een nauwkeuriger schatting van de integraal van `f` op `[0,5]`.
- Bereken zonder gebruik te maken van onder- en bovensommen de bedoelde integraal. Gebruik daarbij wat meetkundige kennis.
-
In Voorbeeld 2 wordt een integraal met de grafische rekenmachine benaderd.
- Verdeel het interval `[1,5]` in acht gelijke delen en bepaal de onder- en de bovensom.
- Ga na, dat de waarde die de rekenmachine voor de integraal van `f` op het interval `[1,5]` vindt tussen de ondersom en de bovensom in ligt.
- Bekijk nu de gegeven functie op het interval `[0,2]`. Bepaal met je grafische rekenmachine de integraal van `f` over dat interval.
- Verdeel het interval `[0,2]` in `n` gelijke deelintervallen. Stel nu een formule op voor de ondersom op dat interval.
- Gebruik de formule `Sigma_(k=1)^(n) k^2 = (n(n + 1)(2n + 1))/6` en toon aan dat de ondersom gelijk is aan `(2(n - 1)(2n - 1))/(3n^2)`.
- Bepaal met behulp van de gevonden formule voor de ondersom de exacte waarde van de integraal van `f` over het interval `[0,2]`.
-
Het verschil tussen een integraal en de oppervlakte ingesloten door de grafiek van een functie en de `x`-as wordt in Voorbeeld 3 besproken.
- Controleer zelf met je grafische rekenmachine dat `int_(0)^(2pi) sin(x) text(d)x = 0`.
- Ga ook na dat `int_(0)^(pi) sin(x) text(d)x = 2`.
- Hoeveel is dus `int_(0)^(0,5pi) sin(x) text(d)x`?
- Hoe groot is de oppervlakte ingesloten door de grafiek van `f(x) = sin(x)`, de `x`-as en de lijn `x = 1,5pi`?
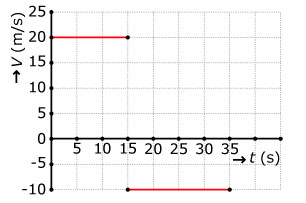
De linker grafiek geeft de snelheid weer van een voorwerp dat langs een rechte weg voortbeweegt.
- Welke betekenis heeft het feit dat de snelheid na 15 seconden negatief is geworden?
- Hoe ver is het voorwerp na 35 seconden van zijn beginpunt verwijderd?
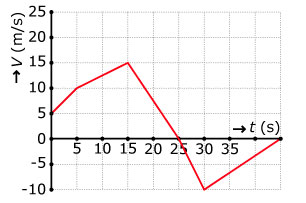
Een ander voorwerp beweegt langs dezelfde rechte weg. De snelheid ervan verandert echter verandert echter voortdurend volgens de rechter grafiek.
- Leg uit, waarom de totale afgelegde afstand vanaf `t = 0` de integraal van de functie `v(t)` is.
- Geef een zo goed mogelijke schatting van de totale afgelegde afstand.
Verwerken
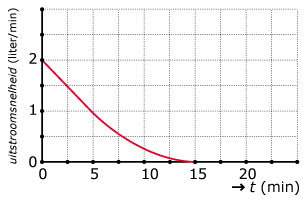 Uit een vat stroomt aan de onderkant olie. In het begin is de uitstroomsnelheid het grootst omdat dan de oliedruk op de bodem het grootst is.
In de grafiek zie je hoe de uitstroomsnelheid varieert. In de eerste vijf minuten neemt de snelheid bij benadering lineair af.
Uit een vat stroomt aan de onderkant olie. In het begin is de uitstroomsnelheid het grootst omdat dan de oliedruk op de bodem het grootst is.
In de grafiek zie je hoe de uitstroomsnelheid varieert. In de eerste vijf minuten neemt de snelheid bij benadering lineair af.
- Welke betekenis heeft de oppervlakte onder deze grafiek?
- Hoeveel olie is er tijdens de eerste vijf minuten uit het vat gestroomd?
- Schat de totale uitgestroomde hoeveelheid olie. Verdeel daarvoor het interval [5, 15] in vier gelijke delen.
- Op welk tijdstip is er 4 liter uit het vat gestroomd?
-
Bekijk de grafiek van de functie `f(x) = sqrt(x)` op het interval `[0,9]`.
- Verdeel het interval [1,9] in vier gelijke deelintervallen, en bepaal de onder- en bovensom bij deze verdeling.
- Geef een schatting van de oppervlakte tussen de grafiek van f (x) en de x-as op het interval [1,9].
- Verdeel het interval [1,9] in acht gelijke intervallen en bepaal de onder- en de bovensom bij deze verdeling.
- Kun je nu de schatting van de oppervlakte aanpassen?
- Hoe groot zijn de onder- en de bovensom als je het interval in 100 gelijke deelintervallen verdeelt?
-
Bereken (waar nodig met je grafische rekenmachine) de volgende integralen.
- `int_(2)^(5) (1 + x) text(d)x`
- `int_(2)^(5) (1 + x)^2 text(d)x`
- `int_(0)^(1,5pi) cos(x) text(d)x`
- `int_(-2)^(2) 1 text(d)x`
- `int_(0)^(1) 2^x text(d)x`
- `int_(3)^(5) sqrt(2x - 6) text(d)x`
-
Gegeven is de functie `f` door `f(x) = x^2 - 8x`.
- Bereken de oppervlakte van het gebied tussen de grafiek van `f` en de `x`-as op het interval `[2,6]`.
- Bereken de oppervlakte van het gebied tussen de grafiek van `f` en de `x`-as op het interval `[6,10]`.
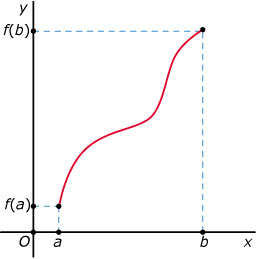 Als een functie `f`overal stijgend of overal dalend is op een interval dan bestaat er een formule waarmee je het verschil tussen onder- en bovensom kunt bepalen.
Die formule bepaalt de nauwkeurigheid van de benadering. Teken een stijgende functie op een interval `[a,b]` zoals hiernaast.
Als een functie `f`overal stijgend of overal dalend is op een interval dan bestaat er een formule waarmee je het verschil tussen onder- en bovensom kunt bepalen.
Die formule bepaalt de nauwkeurigheid van de benadering. Teken een stijgende functie op een interval `[a,b]` zoals hiernaast.
- Verdeel `[a,b]` in vier gelijke delen en teken in de grafiek de rechthoeken die horen bij de ondersom en de rechthoeken die bij de bovensom horen.
Je kunt het interval `[a,b]` in `n` gelijke deelintervallen verdelen.
Altijd is het verschil tussen de onder- en de bovensom gelijk aan het verschil in oppervlakte van twee rechthoeken.
- Welke rechthoeken zijn dat en hoe groot is dat verschil bij `n = 4`?
- Hoe groot is het verschil tussen onder- en bovensom bij een benadering met 10 rechthoeken? En bij `n` rechthoeken?
Een voorbeeld van een stijgende functie is de sinusfunctie op het interval `[0, 1/2 pi]`.
- Voor welke waarde van `n` is het verschil tussen onder- en bovensom kleiner dan 0,0001?
Testen
-
Gegeven is de functie `f` door `f(x) = 4 - x^2` op het interval `[-4,4]`.
- Verdeel dit interval in 8 gelijke deelintervallen en bereken de onder- en de bovensom van de functie.
- Bereken de integraal met behulp van je grafische rekenmachine en laat zien dat dit getal tussen de onder en de bovensom in ligt.
- Bereken de oppervlakte tussen de grafiek van `f` en de `x`-as op het gegeven interval.
-
Gegeven is de derdegraads functie `f(x) = x^3` met domein `[0,2]`.
- Verdeel het interval `[0,2]` in vier gelijke delen en bepaal de ondersom en de bovensom van `f` op dit interval.
- Je kunt het interval ook in `n` gelijke deelintervallen verdelen. Laat zien dat dan de ondersom gelijk is aan:
`bar(S_n) = sum_(k=0)^(n-1) 16/(n^4) * k^3`
- Bepaal met de grafische rekenmachine de ondersom voor `n = 999`.
- Laat zien dat het verschil tussen boven- en ondersom gelijk is aan `16/n`.
- Hoe groot moet je `n` kiezen om zeker te weten dat de eerste drie decimalen in de ondersom kloppen?
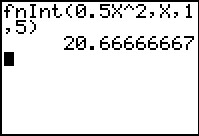 De oppervlakte van V is:
De oppervlakte van V is:




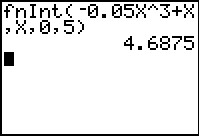
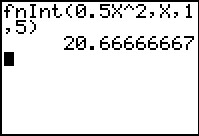





 Uit een vat stroomt aan de onderkant olie. In het begin is de uitstroomsnelheid het grootst omdat dan de oliedruk op de bodem het grootst is.
In de grafiek zie je hoe de uitstroomsnelheid varieert. In de eerste vijf minuten neemt de snelheid bij benadering lineair af.
Uit een vat stroomt aan de onderkant olie. In het begin is de uitstroomsnelheid het grootst omdat dan de oliedruk op de bodem het grootst is.
In de grafiek zie je hoe de uitstroomsnelheid varieert. In de eerste vijf minuten neemt de snelheid bij benadering lineair af.
 Als een functie `f`overal stijgend of overal dalend is op een interval dan bestaat er een formule waarmee je het verschil tussen onder- en bovensom kunt bepalen.
Die formule bepaalt de nauwkeurigheid van de benadering. Teken een stijgende functie op een interval `[a,b]` zoals hiernaast.
Als een functie `f`overal stijgend of overal dalend is op een interval dan bestaat er een formule waarmee je het verschil tussen onder- en bovensom kunt bepalen.
Die formule bepaalt de nauwkeurigheid van de benadering. Teken een stijgende functie op een interval `[a,b]` zoals hiernaast.