Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Totaalbeeld > Samenvatten


Je hebt nu alle basisregels voor het differentiëren geleerd. Het is nuttig om nog even alle begrippen op een rijtje te zetten voor jezelf.

Begrippenlijst:

31: somregel — constante-regel — machtsregel voor gehele positieve n
32: samengestelde functie (kettingfunctie) — kettingregel
33: productfunctie — productregel
34: gebroken functie — quotiëntregel
35: differentieerbaarheid — knikpunt — sprong in grafiek — verticale raaklijn

Activiteitenlijst:

31: differentiëren met de basisregels
32: differentiëren met de kettingregel en de algemene machtsregel
33: differentiëren met de productregelregel
34: differentiëren met de quotiëntregel
35: onderzoek of een functie voor een bepaalde x differentieerbaar is
36: toepassingen van differentiaalrekening

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Totaalbeeld > Achtergronden

Testen

Opgaven

  1. Differentieer de volgende functies.
    1. `f(x) = sqrt(x^2 + 1)`
    2. `f(x) = 4x sqrt(x^2 + 1)`
    3. `f(x) = (4x)/(x^2 + 1)`
    4. `f(x) = (x^2 + 1)/(4x)`
    5. `f(x) = (4x)/sqrt(x^2 + 1)`

  2. In een chemisch proces zijn druk `p` en volume `V` afhankelijk van de tijd `t`. Er geldt: `p(t)=13/(V(t))`. Verder is `V(2)=3` en `p'(t)=2` voor elke waarde van `t`. Op `t=0` is de druk `p(0)=1`.
    1. Bereken `V'(2)`.
    2. Stel een functievoorschrift op voor `V(t)`.

  3. Gegeven is de functie `f(x)=(15x)/(x^2 + 36)`.
    1. Bereken algebraïsch de extremen van `f`.
    2. Toon aan dat `f(-x) = - f(x)` en leg uit welke meetkundige betekenis dit heeft voor de grafiek van `f`.
    3. De raaklijn aan de grafiek van `f` in het punt met `x`-coördinaat 3 snijdt de `y`-as in punt `A`. Stel een vergelijking van die raaklijn op en bereken de coördinaten van `A`.
    4. Er zijn twee getallen `a` en `b` waarvoor geldt: `a * b = 36`. Bewijs dat `f(a) = f(b)`.

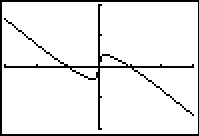  4. Je ziet hier de grafiek van de functie `f(x) = -x + root3(x)`.
    1. Bereken met behulp van differentiëren de extremen van `f` in twee decimalen nauwkeurig.
    2. Voor welke waarde van `x` is de functie `f` niet differentieerbaar? Welke raaklijn heeft de grafiek van `f` in het bijbehorende punt van de grafiek?
    3. Er is een raaklijn aan de grafiek van `f` die door `(0,1)` gaat. Welke richtingscoëfficiënt heeft deze raaklijn?

  5. De functie f is gegeven door:
    `f(x)={((x^2 + 2)/x, text{als } x < -2 vv x > 2),(ax^3 + bx, text{als } -2 <= x <= 2):}`
    1. Neem `a=1` en `b=-2,5`. Onderzoek of deze functie differentieerbaar is voor elke waarde van `x`.
    2. Er zijn waarden voor `a` en `b` te vinden waarbij deze functie wel differentieerbaar is. Bereken deze waarden van `a` en `b`.

  6. Zwemmer in nood

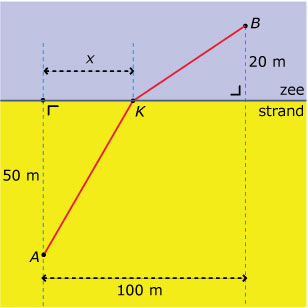    Een zwemmer is in nood voor de kust van Bergen. De tekening geeft een beeld van de situatie. De zwemmer in nood bevindt zich bij punt B in zee. Een lid van de reddingsbrigade ziet de zwemmer in nood en wil in actie komen. Zij bevindt zich in punt A. Ze wil natuurlijk via de snelste weg naar de drenkeling toe. Maar wat is de snelste weg?
    Een deel van de weg moet ze rennend afleggen en een deel zwemmend. Ze rent met een gemiddelde snelheid van 6 m/s en ze zwemt met een gemiddelde snelheid van 1,5 m/s. Hoe kan ze het snelst hulp bieden? Noem het punt waar ze in het water stapt `K`.
    Punt `K` kan overal langs de aangegeven 100 m-lijn liggen. De tijd die ze nodig heeft om in B te komen moet natuurlijk zo klein mogelijk zijn. Noem de totale tijd `t`, de gemiddelde snelheid over het strand `v_s` en de gemiddelde snelheid in zee `v_z`.
    1. Druk `t` uit in `AK`, `KB`, `v_s` en `v_z`.
    2. Formuleer een verband tussen `t` en `x`.
    3. Bepaal met behulp van differentiëren de minimale tijd die ze nodig heeft om de zwemmer te bereiken.
    4. Bepaal de kortste weg.

Toepassen

  1. File

    Als in een min of meer constante stroom auto's met ongeveer dezelfde snelheid wordt geremd, kan er een file ontstaan. Lees hierover meer bij

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Totaalbeeld > Achtergronden

    Stel je nu voor dat door werkzaamheden een rijstrook op de snelweg is afgesloten. Bij het invoegen van auto's naar één rijstrook moet vaak onhandig worden gemanoevreerd, zodat het verkeer moet afremmen of zelfs stil moet staan. Dit is het moment dat een file ontstaat. Zo'n file is niet nodig als iedereen tijdig de juiste doorstroomsnelheid kiest. Daarbij gaat het erom dat zoveel mogelijk auto's per tijdseenheid de wegversmalling passeren. Neem aan dat alle auto's 4 m lang zijn en hun onderlinge afstand precies de remweg `R` (in meter) is. Deze remweg hangt af van de snelheid `v` (in km/h).
    Er geldt bij benadering: `R = 3/4 * (v/10)^2`.
    De verkeersdienst zet een teller halverwege de wegversmalling die meet hoeveel auto's er per minuut passeren. Stel nu een formule op voor het aantal auto's dat per minuut de teller passeert. Bereken met behulp van differentiëren bij welke snelheid zoveel mogelijk auto's de teller passeren.

  2. Spiegel

    Dit is een beroemd probleem uit de Griekse Oudheid. Het stamt uit de Catoptrica van Heroon.

    Een lichtstraal loopt van punt naar punt doordat hij van het oppervlak van een vlakke spiegel wordt teruggekaatst. Aangenomen dat het licht altijd de kortste route neemt, waar raakt het dan de spiegel?

    Bekijk

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Totaalbeeld > Achtergronden

    `P` is het punt waar het licht wordt weerkaatst. De afmetingen zijn verder in de figuur te vinden. De lengte van de lichtstraal (`L`) is gelijk aan de som van de lengtes van `AP` en `PB`. De positie van `P` is bekend als `x` is berekend.
    1. Stel zelf een formule op voor `L` als functie van `x`.
    2. Neem `a = 2` dm, `b = 1` dm en `c = 5` dm. Bereken met behulp van differentiëren `x` als `L` zo klein mogelijk is in twee decimalen nauwkeurig.
    3. Laat ook zien hoe je dit probleem meetkundig kunt oplossen.

Examenopgaven

  1. Verschuivend zwaartepunt

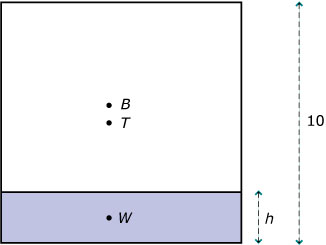
    Een kubusvormige bak met deksel heeft binnenmaten 10 bij 10 bij 10 centimeter en weegt 1 kilogram. Het zwaartepunt van de bak ligt in het centrum van de bak, dus 5 cm boven het midden van de bodem. De bak wordt met water gevuld tot een hoogte van `h` cm. Het zwaartepunt van het water (de bak niet meegerekend) ligt in het centrum van het water, dus `1/2 h` cm boven het midden van de bodem. Zie de foto en de figuur waarin op schaal een vooraanzicht van de bak is getekend. Het zwaartepunt van het geheel (bak en water samen) noemen we `T`. Het punt `T` ligt op het lijnstuk `BW`. Er geldt: `d_T=h/(h+10)d_w+10/(h+10)d_b`. Hierbij zijn `d_T`, `d_W` en `d_B` de afstand in centimeter van achtereenvolgens `T, W` en `B` tot de bodem.
    1. Bereken `d_T` voor `h=3`. Geef je antwoord in één decimaal nauwkeurig.
    2. Toon aan dat voor de afstand van tot de bodem, uitgedrukt in `h`, geldt: `d_T=(h^2+100)/(2h+20)`.
    3. Als de bak leeg is, valt `T` samen met `B`. Tijdens het vullen van de bak verschuift de plaats van `T` eerst omlaag en later weer omhoog. Als de bak vol is, valt `T` weer samen met `B`. Bereken voor welke waarden van `h` geldt: `d_T < 4,5`. Geef je antwoord in één decimaal nauwkeurig.
    4. Bereken exact voor welke waarde van `h` de afstand van `T` tot de bodem minimaal is.

    (bron: examen wiskunde B vwo 2002, eerste tijdvak)


  2. Kortste weg

    We bekijken de lijn met vergelijking `y = mx`, met `m > 0`. De lijn snijdt de lijn `y = -2` in `A` en de lijn `x = 4` in `B`.



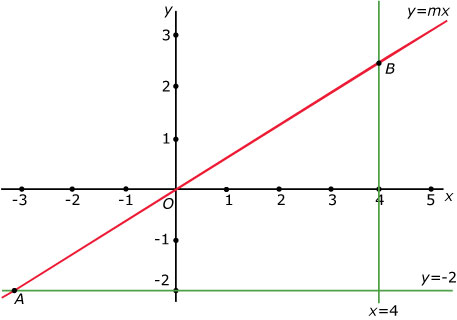
    1. Bewijs dat voor elke positieve waarde van `m` de lengte van het lijnstuk gelijk is aan `sqrt((4m+2)^2+(2/m +4)^2)`.
    Plaats `P` ligt dichtbij het kruispunt van twee wegen, de `H25` en de `V18`. De wegen snijden elkaar loodrecht. Plaats `P` ligt 4 km van de `H25` en 7 km van de `V18` af. Er wordt een nieuwe rechte weg aangelegd die de twee wegen met elkaar verbindt. De nieuwe weg moet door plaats `P` gaan.



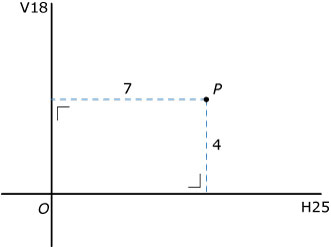
    1. Bereken in meters nauwkeurig de lengte van de kortste weg die aan deze eisen voldoet.

    (bron: examen wiskunde B vwo 2002, tweede tijdvak)


  3. Kogelbanen

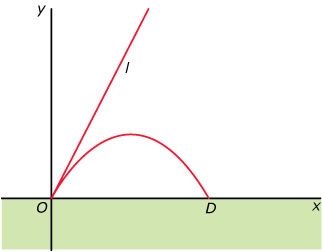
    Vanuit een bepaald punt worden kogels afgeschoten met steeds dezelfde beginsnelheid. De hoek waaronder men de kogels afschiet, varieert. We brengen een assenstelsel aan in het vlak van de kogelbaan, met de `x`-as horizontaal en de `y`-as verticaal. De kogels worden afgeschoten in het punt `(0,0)` en komen neer in een punt op de `x`-as. Zie de bovenste figuur. In deze figuur is behalve de kogelbaan ook de raaklijn `l` in `(0,0)` aan deze baan getekend. De kogel wordt weggeschoten in de richting van `l`. Uit de mechanica is bekend dat een kogelbaan een deel van een parabool is. Een vergelijking van de kogelbaan is: `y = rx - (0,1 + 0,1r^2)x^2`. Hierbij is `r` een constante die afhangt van de hoek waaronder geschoten wordt.
    1. De richtingscoëfficiënt van `l` is gelijk aan `r`. Toon dit aan.
    2. Er geldt: `OD = (10r)/(1 + r^2)`. Toon dit aan.
    3. Bereken met behulp van differentiëren voor welke waarde van `r` de afstand maximaal is.
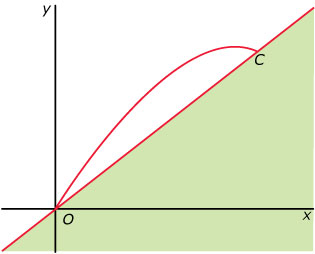
    4. Veronderstel dat de kogel niet op een horizontaal terrein wordt afgeschoten, maar op een hellend terrein met richtingscoëfficiënt 1. Zie de onderste figuur. Het hangt van `r` af waar de kogel op het terrein neerkomt. Dit punt noemen we `C`. De `x`-coördinaat van punt `C` is `(10(r - 1))/(1 + r^2)`. Bereken de maximale lengte van `OC` in twee decimalen nauwkeurig.

    (bron: examen wiskunde B vwo 2003, tweede tijdvak)