Toepassingen

Inleiding

Een model is een vereenvoudigde weergave van de werkelijkheid.
In de wetenschap wordt veel met modellen gewerkt omdat de werkelijkheid te complex is om zonder meer te beschrijven. Door niet belangrijke details weg te laten (verstandige aannames te doen) kan een model worden opgesteld dat met wiskundige middelen is te beschrijven en door te rekenen. Uit het doorrekenen van het model worden conclusies getrokken die dan weer kunnen worden vergeleken met de realiteit.
Bij het werken met modellen gaat het vaak om het berekenen van extremen, om "optimaliseringsproblemen". Daarbij wordt het differentiëren toegepast. En er zijn nog andere toepassingen van differentiëren...

Je leert nu:

• werken met modellen waarin het differentiëren kan worden toegepast;
• optimaliseringsproblemen aanpakken;
• raaklijn opstellen door een punt buiten de grafiek.

Je kunt al:

• differentiëren met alle differentieerregels;
• werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.

Verkennen

Een blikfabriek maakt onder andere cilindervormige blikken voor de conservenindustrie. Er is veel vraag naar blikken met een inhoud van 1 liter. Voor de fabrikant is het belangrijk dat daar zo min mogelijk blik voor nodig is, dan blijven zijn kosten laag.

> Welke afmetingen zal hij zijn literblikken geven?

Uitleg

Een blikfabriek maakt onder andere cilindervormige blikken voor de conservenindustrie. Er is veel vraag naar blikken met een inhoud van 1 liter. Voor de fabrikant is het belangrijk dat daar zo min mogelijk blik voor nodig is, dan blijven zijn kosten laag.
Welke afmetingen zal hij zijn literblikken geven?

Eerst een rekenmodel opstellen:
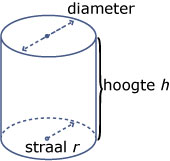
Neem aan dat elk blik zuiver cilindrisch is en dat de benodigde hoeveelheid blik gelijk is aan de totale oppervlakte van het blik. De twee bepalende variabelen zijn dan de straal van (het grondvlak van) het blik r en de hoogte h, neem beide in cm. Het gegeven betreft de inhoud van een blik (1 L = 1000 cm³), de eis betreft de oppervlakte die minimaal moet zijn.
Voor de inhoud van een cilinder geldt: I = πr²h.
Voor de oppervlakte van een cilinder geldt: A = 2πrh + 2πr².
Ga dat na.

Met I = 1000 vind je 1000 = πr²h en dus: $h=\frac{1000}{\pi r^2}$.
Als je nu in de formule voor A deze uitdrukking invult voor h, dan vind je: $A(r)=\frac{2000}{r}+2\pi r^2$.

Met behulp van differentiëren of de grafische rekenmachine vind je nu dat voor x ≈ 5,4 cm en h ≈ 10,8 cm de totale oppervlakte minimaal is.

Opgaven

1. In de Uitleg zie je een globale uitwerking van het probleem van het cilindervormige literblik met een zo klein mogelijke oppervlakte.
   1. Welke aannames worden er gedaan?
   2. Hoe kom je aan de formule voor de oppervlakte van het blik?
   3. Laat zien hoe je de formule voor `A(r)` kunt afleiden.
   4. Bepaal nu de afgeleide van `A(r)` en bereken met behulp daarvan de waarde van `r` waarvoor `A(r)` minimaal is.

Theorie

Wiskunde wordt veel toegepast in wetenschap en handel en industie om problemen op te lossen.
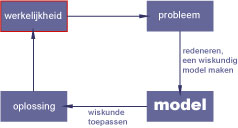
Daarmee wordt bedoeld dat bij een wetenschappelijk onderzoek, een nieuw te ontwikkelen technologie, een productieproces, en dergelijke vanuit de al bestaande praktijk een vraagstuk naar voren komt waar een antwoord op moet worden gevonden. Vaak heeft dat antwoord de vorm van een wiskundig model.
Een wiskundig model is een vereenvoudiging van de werkelijkheid op grond van verstandige aannames. In een goed model zijn alle belangrijke factoren nog aanwezig, alleen de onbelangrijke blijven buiten beschouwing. Meestal heeft het model de vorm van één of meer formules die beschrijven hoe de belangrijke variabelen zich gedragen.
Op die formules wordt dan de geschikte wiskundige theorie losgelaten...

Meer hierover vind je bij de rubriek "Probleemaanpak" op deze website.

Bij optimaliseren gaat het om wiskundige modellen waarbij wordt gezocht naar een maximale of een minimale waarde. Vaak is dat het maximum of minimum van een functie. Je kunt dat vinden met behulp van differentiëren of met je grafische rekenmachine.

Voorbeeld 1

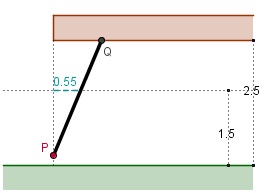
Je ziet hier een dwarsdoorsnede van een garage met een garagedeur. Bij het openen van de deur gaat de onderkant recht omhoog, terwijl de bovenkant langs het plafond horizontaal naar binnen gaat. Binnen in de garage moet dus voldoende ruimte zijn om te zorgen dat een auto niet beschadigd raakt door de naar binnen komende deur. De garagedeur is 2,50 m hoog en je auto is 1,50 m hoog. Hoe ver komt de deur op die hoogte van 1,50 m maximaal naar binnen?

Antwoord

Noem de afstand van P tot het plafond x en de afstand die de deur op een hoogte van 1,50 m naar binnen komt A, beide in m. Je kunt dan met behulp van gelijkvormige rechthoekige driehoeken afleiden:
$A(x)=\left(\frac{x-1}{x}\right)\sqrt{{\mathrm{2,5}}^2-x^2}$

Door A'(x) = 0 op te lossen vind je: x ≈ 1,84 m.
En omdat A(1,84) ≈ 0,77 m, komt de garagedeur op een hoogte van 1,50 m zo'n 77 cm naar binnen.

Voorbeeld

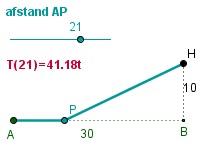
Naar punt H van een woonhuis moet een nieuwe leiding worden gegraven vanuit het aansluitingspunt A. Nu kost het graven en weer netjes dichtmaken van een sleuf in de tuin 1,5 keer zoveel tijd als datzelfde werk langs de wegkant AB. Hoe moet er worden gegraven om alles in zo kort mogelijke tijd te doen?

Antwoord

Neem x m voor de lengte van BP.
Ga na, dat dan 30 – x de lengte van AP en $\sqrt{x^2+100}$ de lengte van PH is.

Als t de benodigde tijd per m langs de weg is, is 1,5t de benodigde tijd per m door de tuin.
De totale benodigde tijd T is daarom: T(x) = t(30 – x) + 1,5t $\sqrt{x^2+100}$.
Met behulp van differentiëren vind je de waarde van x waarvoor T maximaal is. Je ziet waarschijnlijk wel dat de waarde van t daarbij geen enkele rol speelt.

Voorbeeld 3

Gegeven is de functie f door f(x) = $x+\frac{1}{x}$.
Stel een vergelijking op van de raaklijnen aan de grafiek van f die door het punt P(2,1) gaan.

Antwoord

Bekijk de bijbehorende applet op

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentieerregels > Voorbeeld 3

Je ziet in de figuur dat lijn l de grafiek raakt als de helling van die lijn gelijk is aan de helling van de grafiek (de afgeleide dus) van de functie f.
Het raakpunt is (x,f(x)), dus:
$f\text{'}(x)=\frac{f(x)-1}{x-2}$.
(Let hierbij goed op mintekens!)

f(x) = $x+\frac{1}{x}$ en $f\text{'}(x)=1-\frac{1}{x^2}$ geeft:
$1-\frac{1}{x^2}=\frac{x+\frac{1}{x}-1}{x-2}$.
Ga na, dat dit oplevert: x = –1 – $\sqrt{3}$  V  x = –1 + $\sqrt{3}$.

En hiermee kun je de mogelijke raakpunten bepalen en de vergelijkingen van beide mogelijke raaklijnen opstellen.

Opgaven

2. Bekijk het probleem in Voorbeeld 1.
   1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
   2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan zelf de formule voor `A(x)` af te leiden.
   3. Bereken met behulp van differentiëren voor welke `x` de waarde van `A` maximaal is.


3. Bekijk het probleem in Voorbeeld 2.
   1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
   2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan de gegeven formule voor `T(x)` af te leiden.
   3. Bereken met behulp van differentiëren voor welke `x` de waarde van `T` minimaal is.


4. In Voorbeeld 3 tref je een zuiver wiskundig probleem aan om op te lossen. Van het opstellen van een rekenmodel is nu geen sprake, van het vinden van een juiste aanpak wel.
   1. Ga eerst met de applet na (door punt `A` te verplaatsen) dat er twee van die raaklijnen mogelijk zijn. Schat de coördinaten van de punten op de grafiek waar die raaklijnen door gaan.
   2. Probeer nu eerst zelf een oplossing voor het probleem te vinden.
   3. Bestudeer nu de oplossing die wordt geschetst bij "Antwoord" en reken deze oplossing na. Probeer elke stap te verklaren.
   Je had dit probleem ook anders kunnen aanpakken, bijvoorbeeld door het punt `A` variabele coördinaten te geven: `A(a,a + 1/a)`. Als je niet zelf zo'n oplossing hebt gevonden, loop dan de volgende stappen door.
   4. Leg uit dat dan de richtingscoëfficiënt van de raaklijn door `A` gelijk is aan `1 - 1/(a^2)`.
   5. Je kunt nu de vergelijking van de raaklijn door `A` met die richtingscoëfficiënt opstellen. Laat zien hoe.
   6. Bereken tenslotte de twee mogelijke waarden voor `a` door gebruik te maken van het gegeven dat de raaklijn door `P(2,1)` moet gaan.


5. Gegeven zijn de functies `f` en `g` door `f(x) = x^2` en `g(x) = sqrt(x)`.
   De lijn `x = p` met `0 < p < 1` snijdt beide grafieken in de punten `A` en `B`. Voor welke waarde van `p` is de lengte van lijnstuk `AB` maximaal?
   

Verwerken

6. Op rechthoekige vellen papier van 1 m² worden foto’s afgedrukt om posters te maken. Om de foto blijft een rand wit: aan de onderkant een strook van 2 dm breedte, aan de andere drie randen stroken van 1 dm breedte.
   Bij welke afmetingen van de poster wordt de oppervlakte van het bedrukte deel zo groot mogelijk?
   1. Maak zelf een schets van de situatie met de gegevens er in.
   2. Probeer eerst zelf het probleem op te lossen. Kijk pas als dat niet lukt naar c en d.
   3. Neem aan dat de breedte van zo’n poster wordt voorgesteld door `x` dm. Leid een formule af voor de oppervlakte `A` van het bedrukte deel als functie van `x`.
   4. Bereken met behulp van differentiëren de waarde van `x` waarvoor `A(x)` maximaal is.
   5. Beantwoord tenslotte de aan het begin gestelde vraag.



7. Ladderprobleem

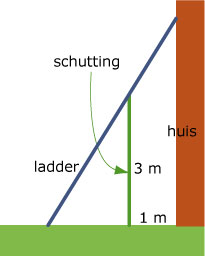   Iemand wil een ladder kopen om zijn dakgoten schoon te maken. Vlak naast zijn huis op 1 m van de muur staat echter een schutting van 3 m hoog. Hoe lang moet een ladder minstens zijn om over de schutting tegen de muur van het huis te komen?
   (Ga er van uit dat zowel de muur van het huis als de schutting loodrecht op de vlakke grond staan.)
   



8. Grootste gelijkbenige driehoek

   Hoe lang zijn de zijden van de gelijkbenige driehoek met de grootste oppervlakte die een omtrek heeft van 20 cm?
   


9. Bekijk de grafiek van de functie f met `f(x) = (100x^2 - 400)/(x^4 + 100)`.
   1. Bereken algebraïsch het bereik van `f`. Geef benaderingen in één decimaal nauwkeurig.
   2. Los algebraïsch op: `f(x) <= (1)/(f(x))`.
   3. De lijn `y = ax` raakt de grafiek van `f`. Bereken `a`.


10. Gegeven is de familie van functies `f_p` door `f_(p)(x) = (x^2 + px + 4)/(x + 3)`.
    1. Bereken algebraïsch de nulpunten en de extremen van `f_4`.
    2. Voor welke waarden van `p` heeft de grafiek van `f_p` geen verticale asymptoot?
    3. Voor welke waarden van `p` heeft de grafiek van `f_p` geen nulpunten?
    4. Voor welke waarden van `p` heeft `f_p` geen extremen?
    5. Voor welke waarden van `p` gaat de raaklijn aan de grafiek van `f_p` voor `x = 0` door het punt `(9, 1/3)`?


11. In een rechthoekig `Oxy`-assenstelsel snijdt lijn `x = p` met `p > 0` de grafiek van `f(x) = 4 - x^2` in punt `P`.
    1. Bereken de minimale waarde die lijnstuk `OP` kan aannemen.
    Neem nu aan dat `0 < p < 2`. De lijn `x = p` snijdt de `x-as` in `A` en van de rechthoek `APQB` liggen de punten `P` en `Q` op de grafiek van `f` en ligt punt `B` ook op de `x`-as.
    2. Bereken de maximale waarde die de oppervlakte van rechthoek `APQB` kan aannemen.
    Een cirkel met middelpunt `O` raakt de grafiek van `f` in twee punten.
    3. Bereken de straal van deze cirkel.

Testen

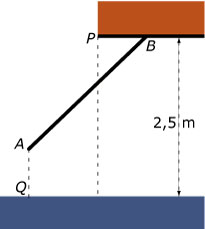12. Hier zie je een bewegende garagedeur. De hoogte van punt `A` (de onderkant van de deur) boven de grond is in elke stand even groot als de lengte van `PB`.
    Bereken algebraïsch hoe ver de onderkant van de deur maximaal naar buiten komt. Geef je antwoord in één decimaal nauwkeurig.
    


13. Gegeven is de functie `f` met `f(x) = (x^2 - x)^4`.
    1. Bepaal algebraïsch de extremen van `f`.
    2. De lijn met vergelijking `x = k` met `0 < k < 1` snijdt de `x`-as in `A` en de grafiek van `f` in `B`.Voor welke waarde van `k` is de oppervlakte van `Delta OAB` maximaal?