Toepassingen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Toepassingen > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden. Bij de Uitleg vind je een globale uitwerking voor het geval je er helemaal niet uit komt.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Toepassingen > Uitleg

Bestudeer de Uitleg.

Opgaven

  1. In de Uitleg zie je een globale uitwerking van het probleem van het cilindervormige literblik met een zo klein mogelijke oppervlakte.
    1. Welke aannames worden er gedaan?
    2. Hoe kom je aan de formule voor de oppervlakte van het blik?
    3. Laat zien hoe je de formule voor `A(r)` kunt afleiden.
    4. Bepaal nu de afgeleide van `A(r)` en bereken met behulp daarvan de waarde van `r` waarvoor `A(r)` minimaal is.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Toepassingen > Theorie

Bestudeer eerst de Theorie. Bekijk goed wat een wiskundig model is. Bij de rubriek "Probleemaanpak" vind je meer over dit onderwerp.

Opgaven

  1. Bekijk het probleem in Voorbeeld 1.
    1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
    2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan zelf de formule voor `A(x)` af te leiden.
    3. Bereken met behulp van differentiëren voor welke `x` de waarde van `A` maximaal is.

  2. Bekijk het probleem in Voorbeeld 2.
    1. Probeer eerst om (zonder naar het antwoord te kijken) zelf een oplossing te vinden.
    2. Bekijk nu de oplossing die bij "Antwoord" wordt gegeven. Als je zelf een andere of geen oplossing hebt gevonden, probeer dan de gegeven formule voor `T(x)` af te leiden.
    3. Bereken met behulp van differentiëren voor welke `x` de waarde van `T` minimaal is.

  3. In Voorbeeld 3 tref je een zuiver wiskundig probleem aan om op te lossen. Van het opstellen van een rekenmodel is nu geen sprake, van het vinden van een juiste aanpak wel.
    1. Ga eerst met de applet na (door punt `A` te verplaatsen) dat er twee van die raaklijnen mogelijk zijn. Schat de coördinaten van de punten op de grafiek waar die raaklijnen door gaan.
    2. Probeer nu eerst zelf een oplossing voor het probleem te vinden.
    3. Bestudeer nu de oplossing die wordt geschetst bij "Antwoord" en reken deze oplossing na. Probeer elke stap te verklaren.
    Je had dit probleem ook anders kunnen aanpakken, bijvoorbeeld door het punt `A` variabele coördinaten te geven: `A(a,a + 1/a)`. Als je niet zelf zo'n oplossing hebt gevonden, loop dan de volgende stappen door.
    1. Leg uit dat dan de richtingscoëfficiënt van de raaklijn door `A` gelijk is aan `1 - 1/(a^2)`.
    2. Je kunt nu de vergelijking van de raaklijn door `A` met die richtingscoëfficiënt opstellen. Laat zien hoe.
    3. Bereken tenslotte de twee mogelijke waarden voor `a` door gebruik te maken van het gegeven dat de raaklijn door `P(2,1)` moet gaan.

  4. Gegeven zijn de functies `f` en `g` door `f(x) = x^2` en `g(x) = sqrt(x)`.
    De lijn `x = p` met `0 < p < 1` snijdt beide grafieken in de punten `A` en `B`. Voor welke waarde van `p` is de lengte van lijnstuk `AB` maximaal?

Verwerken

  1. Op rechthoekige vellen papier van 1 m2 worden foto’s afgedrukt om posters te maken. Om de foto blijft een rand wit: aan de onderkant een strook van 2 dm breedte, aan de andere drie randen stroken van 1 dm breedte.
    Bij welke afmetingen van de poster wordt de oppervlakte van het bedrukte deel zo groot mogelijk?
    1. Maak zelf een schets van de situatie met de gegevens er in.
    2. Probeer eerst zelf het probleem op te lossen. Kijk pas als dat niet lukt naar c en d.
    3. Neem aan dat de breedte van zo’n poster wordt voorgesteld door `x` dm. Leid een formule af voor de oppervlakte `A` van het bedrukte deel als functie van `x`.
    4. Bereken met behulp van differentiëren de waarde van `x` waarvoor `A(x)` maximaal is.
    5. Beantwoord tenslotte de aan het begin gestelde vraag.

  2. Ladderprobleem

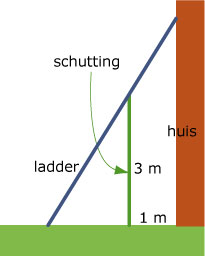    Iemand wil een ladder kopen om zijn dakgoten schoon te maken. Vlak naast zijn huis op 1 m van de muur staat echter een schutting van 3 m hoog. Hoe lang moet een ladder minstens zijn om over de schutting tegen de muur van het huis te komen?
    (Ga er van uit dat zowel de muur van het huis als de schutting loodrecht op de vlakke grond staan.)

  3. Grootste gelijkbenige driehoek

    Hoe lang zijn de zijden van de gelijkbenige driehoek met de grootste oppervlakte die een omtrek heeft van 20 cm?

  4. Bekijk de grafiek van de functie f met `f(x) = (100x^2 - 400)/(x^4 + 100)`.
    1. Bereken algebraïsch het bereik van `f`. Geef benaderingen in één decimaal nauwkeurig.
    2. Los algebraïsch op: `f(x) <= (1)/(f(x))`.
    3. De lijn `y = ax` raakt de grafiek van `f`. Bereken `a`.

  5. Gegeven is de familie van functies `f_p` door `f_(p)(x) = (x^2 + px + 4)/(x + 3)`.
    1. Bereken algebraïsch de nulpunten en de extremen van `f_4`.
    2. Voor welke waarden van `p` heeft de grafiek van `f_p` geen verticale asymptoot?
    3. Voor welke waarden van `p` heeft de grafiek van `f_p` geen nulpunten?
    4. Voor welke waarden van `p` heeft `f_p` geen extremen?
    5. Voor welke waarden van `p` gaat de raaklijn aan de grafiek van `f_p` voor `x = 0` door het punt `(9, 1/3)`?

  6. In een rechthoekig `Oxy`-assenstelsel snijdt lijn `x = p` met `p > 0` de grafiek van `f(x) = 4 - x^2` in punt `P`.
    1. Bereken de minimale waarde die lijnstuk `OP` kan aannemen.
    Neem nu aan dat `0 < p < 2`. De lijn `x = p` snijdt de `x-as` in `A` en van de rechthoek `APQB` liggen de punten `P` en `Q` op de grafiek van `f` en ligt punt `B` ook op de `x`-as.
    1. Bereken de maximale waarde die de oppervlakte van rechthoek `APQB` kan aannemen.
    Een cirkel met middelpunt `O` raakt de grafiek van `f` in twee punten.
    1. Bereken de straal van deze cirkel.

Testen

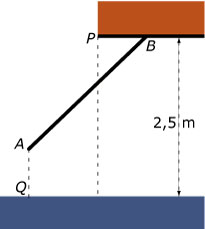  1. Hier zie je een bewegende garagedeur. De hoogte van punt `A` (de onderkant van de deur) boven de grond is in elke stand even groot als de lengte van `PB`.
    Bereken algebraïsch hoe ver de onderkant van de deur maximaal naar buiten komt. Geef je antwoord in één decimaal nauwkeurig.

  2. Gegeven is de functie `f` met `f(x) = (x^2 - x)^4`.
    1. Bepaal algebraïsch de extremen van `f`.
    2. De lijn met vergelijking `x = k` met `0 < k < 1` snijdt de `x`-as in `A` en de grafiek van `f` in `B`.Voor welke waarde van `k` is de oppervlakte van `Delta OAB` maximaal?