Differentieerbaarheid

Inleiding

Je kent nu de meest gebruikte differentieerregels. Het lijkt er op dat je alle functies zonder problemen kunt differentiëren. Dat is echter niet het geval. Er bestaan functies waarbij zelfs binnen het domein problemen optreden met de afgeleide.

In dit onderdeel kom je daar een aantal voorbeelden van tegen. Het gaat dan om sprongen en knikken in de grafiek.

Je leert nu:

• herkennen wanneer en waar een bepaalde functie (zelfs binnen zijn domein) geen afgeleide heeft;
• werken met de afgeleide in de buurt van knikpunten en sprongen in de grafiek.

Je kunt al:

• allerlei soorten functies gebruiken;
• differentiëren met alle basisregels;
• werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.

Verkennen

Bekijk de grafiek van $y=\sqrt{x}$ op je grafische rekenmachine.

> Probeer je grafische rekenmachine het hellingsgetal voor x = 0 te laten vinden.
> Welk probleem doet zich daarbij voor? Kun je er een verklaring voor vinden?
> Heeft deze grafiek een raaklijn voor x = 0? Zo ja, welke vergelijking hoort er dan bij die raaklijn?

Uitleg

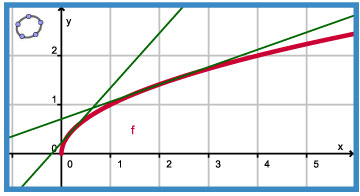
Hier zie je grafiek van f(x) = $\sqrt{x}$.
Het domein van deze wortelfunctie is $[\mathrm{0,}\to \rangle$.
Het randpunt (0, 0) is een punt van de grafiek van f.

De afgeleide is $f\text{'}(x)=\frac{1}{2\sqrt{x}}$.

Hier heeft f'(0) geen betekenis, want je deelt dan door 0 en dat geeft geen reële uitkomst.
Als je de grafiek van f in de buurt van x = 0 nader bekijkt, zie je dat de helling daar heel erg groot is. In (0, 0) is de helling oneindig groot. De grafiek heeft in dat punt een verticale raaklijn met vergelijking x = 0.

Je zegt wel dat deze wortelfunctie niet differentieerbaar is voor x = 0. Ook de meeste andere wortelfuncties kennen waarden waarin de functie niet differentieerbaar is.

Er zijn verschillende situaties denkbaar waarbij een functie voor een bepaalde waarde van x geen afgeleide heeft hoewel die waarde wel tot het domein behoort. Vaak is dat zichtbaar aan een knik in de grafiek of een sprong in de grafiek. Op plaatsen waarin een knik of een sprong optreedt kun je niet precies één raaklijn aan de grafiek tekenen. Ook randpunten van de grafiek kunnen een onbepaalde helling hebben.

Opgaven

1. Je ziet in de Uitleg dat de functie `f(x) = sqrt(x)` niet differentieerbaar is voor `x = 0`.
   1. Wat betekent dit?
   2. Voor welke waarde van `x` is de functie `g` met `g(x) = 2 + sqrt(x - 3)` niet differentieerbaar?
   3. Welke vergelijking heeft de raaklijn aan de grafiek van `g` voor de in b bedoelde waarde van `x`?


2. Je ziet hier de grafiek van de functie `f` met `f(x) = |x|` met `-5 <= x <= 5`.
   1. Welke helling heeft de grafiek van `f` voor `x < 0`?
   2. Welke helling heeft de grafiek van `f` voor `x > 0`?
   3. Waarom is de grafiek van `f` voor `x=0` niet differentieerbaar?
   4. Is de functie `g(x) = |x^3|` voor `x=0` differentieerbaar?

Theorie

Een functie f is differentieerbaar voor x = a als a tot het domein van f behoort en

$f\text{'}(a)=\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}$

bestaat. Belangrijk is hierbij dat h zowel positief als negatief moet kunnen zijn: het naar 0 naderen moet zowel van de negatieve als de positieve kant kunnen en hetzelfde getal opleveren!
Dat differentiaalquotiënt is dan de richtingscoëfficiënt van de raaklijn voor x = a aan de grafiek van f. Het komt er dus op neer, dat je de functie voor x = a precies één hellingsgetal moet kunnen geven en een bijpassende vergelijking van de raaklijn moet kunnen opstellen.

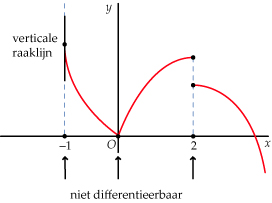
Er zijn verschillende situaties waarin een functie niet differentieerbaar is, terwijl de betreffende x-waarde wel tot het domein van f behoort. Hier zie je daar voorbeelden van. Het gaat om x-waarden waarin de grafiek

• een verticale raaklijn, of
• een knikpunt, of
• een sprong

vertoont.

Voorbeeld 1

Bekijk de grafieken van de functies $f(x)=\sqrt{x-2}$  en $g(x)=\frac{1}{\sqrt{x-2}}$

Hoe zit het met de differentieerbaarheid van beide functies?

Antwoord

Functie f heeft als domein $[\mathrm{2,}\to \rangle$.
Zijn afgeleide $f\text{'}(x)=\frac{1}{2\sqrt{x-2}}$  heeft als domein $\langle \mathrm{2,}\to \rangle$.
Naarmate je dichter bij het randpunt (2, 0) komt, wordt de grafiek steeds steiler. In dit punt heeft de grafiek een verticale raaklijn. De functie f is niet differentieerbaar voor x = 2 hoewel dit getal wel in het domein zit.

Functie g heeft als domein $\langle \mathrm{2,}\to \rangle$.
Zijn afgeleide $g\text{'}(x)=\frac{-1}{2(x-2)\sqrt{x-2}}$  heeft als domein ook $\langle \mathrm{2,}\to \rangle$.
De functie g is voor elke x-waarde in zijn domein differentieerbaar.

Voorbeeld 2

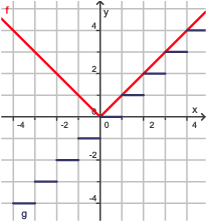
Twee bijzondere functies zijn de absoluutfunctie f(x) = |x| en de integerfunctie g(x) = int(x).
Je ziet hier de grafieken van beide. Hoe zit het met de differentieerbaarheid?

Antwoord

De grafiek van de functie f(x) = |x| bestaat uit twee halve lijnen die in (0, 0) bij elkaar komen. Daar zit een knikpunt. De functie is te schrijven als

$f(x)=\{\begin{array}{cc}x& \text{als }x\ge 0\\ -x& \text{als }x<0\end{array}$
De afgeleide is daarom $f\text{'}(x)=\{\begin{array}{cc}1& \text{als }x\ge 0\\ -1& \text{als }x<0\end{array}$

Je ziet dat het hellingsgetal links van 0 anders is dan rechts van 0.
De functie is voor x = 0 niet differentieerbaar.

De functie g(x) = int(x) rondt steeds een getal naar beneden af. De grafiek vertoont daarom sprongen zodra een x-waarde een geheel getal is.
In die waarden van x is de functie niet differentieerbaar.

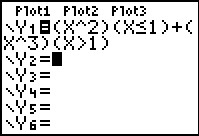
Voorbeeld 3

Soms bestaat een functie uit meerdere delen. Bijvoorbeeld:

$f(x)=\{\begin{array}{cc}{x}^2& \text{als }x\le 1\\ x^3& \text{als }x>1\end{array}$

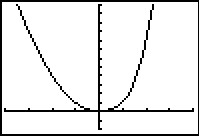
Laat zien dat deze functie niet differentieerbaar is voor x = 1.

Antwoord

De grafiek van f vertoont bij x = 1 geen sprong, want zowel 1² = 1 als 1³ = 1.
De afgeleide is:

$f\text{'}(x)=\{\begin{array}{cc}2x& \text{als }x\le 1\\ 3x^2& \text{als }x>1\end{array}$

Bekijk je nu het punt (1, 1) dan zie je dat het hellingsgetal 2 wordt als je van links naar x = 1 nadert, terwijl het hellingsgetal 3 wordt als je van rechts naar x = 1 gaat.

Omdat beide hellingen verschillend zijn, is er sprake van een knikpunt en is f niet differentieerbaar voor x = 1.

Opgaven

3. Bekijk de twee functies in Voorbeeld 1.
   1. Waarom zijn zowel `f` als `g` niet differentieerbaar voor `x=2`?
   2. Waarom heeft de grafiek van `f` wel een raaklijn voor `x=2` maar de grafiek van `g` niet?


4. Gegeven is de functie `f(x)=root3(x^2)`.
   1. Los op: `f(x)=2`.
   2. Bepaal domein en bereik van `f`.
   3. Bepaal de afgeleide van `f`.
   4. Voor `x=0` is de functie `f` niet differentieerbaar. Dit komt omdat
      1. `f(0)=0` en `f'(0)` niet bestaat;
      2. de grafiek van de functie `f` geen raaklijn heeft voor `x=0`;
      3. de derdemachtswortel uit 0 niet bestaat;
   5. In elk van de punten `A` en `B` waarvoor geldt `y=1` heeft de grafiek van `f` een raaklijn. Bereken het snijpunt van die raaklijnen.


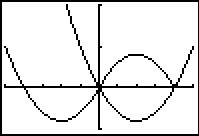5. Hier zie je de grafieken van de functies `f(x)=|x^2-4x|` en `g(x)=x^2-|4x|`. Bekijk eventueel Voorbeeld 2.
   1. Voor welke waarden van `x` is functie `f` niet differentieerbaar?
   2. Voor welke waarden van `x` is functie `g` niet differentieerbaar?


6. In Voorbeeld 2 kun je ook zien hoe de grafiek van de entierfunctie er uit ziet.
   1. Voor welke waarden van `x` is de functie `f(x)=int(2x)` niet differentieerbaar?
      1. Voor alle gehele getallen `x`.
      2. Voor alle veelvouden van 0,5.
      3. Voor alle veelvouden van 2.
   2. Voor welke waarden van `x` is de functie `f(x)=2*int(x)` niet differentieerbaar?
      1. Voor alle gehele getallen `x`.
      2. Voor alle veelvouden van 0,5.
      3. Voor alle veelvouden van 2.


7. Bekijk de grafiek van de functie in Voorbeeld 3.
   1. Maak zelf deze grafiek op je grafische rekenmachine.
   2. Waarom is deze functie niet differentieerbaar voor `x=1`?
   Bekijk nu de functie
   `g(x) = {(x^2, text{als } x < 0), (x^3, text{als } x >= 0):}`
   3. Waarom is `g` wel differentieerbaar voor `x=0`?

Verwerken

8. Bepaal de punten waarin de volgende functies niet differentieerbaar zijn
   1. `f(x) = sqrt(4x - x^2)`
   2. `g(x) = |9 - x^2|`
   3. `h(x) = (sqrt(x + 2))/x`
   4. `k(x) = 2x + |x - 5|`


9. Hier zie je de grafiek van de functie `f(x) = -2x + 3root[3](x^2)` op het domein `[-1,8]`.
   1. Laat zien dat deze functie voor `x=0` niet differentieerbaar is.
   2. Bereken de extremen van deze functie.
   3. De raaklijn voor `x=k` snijdt de `x`-as en de `y`-as in twee punten die evenver van `(0,0)` af liggen. Bereken `k`.


10. De functie `f(x) = x^2|x + 4|` heeft een knikpunt `(-4,0)`.
    In dit knikpunt kun je twee lijnen tekenen die de grafiek van f raken. Bereken de richtingscofficinten van deze twee lijnen.
    


11. Gegeven is de functie f die is gedefinieerd door:
    `f(x) = {(4 - x^2, text{als } x < 1),((x - 2)^2 + 2, text{als } x >= 1):}`
    1. Laat zien dat deze functie voor elke waarde van `x` differentieerbaar is.
    2. Het functievoorschrift wordt voor `x>=1` vervangen door een functievoorschrift van de vorm `f(x)=ax+b`. Welke waarden moeten `a` en `b` dan hebben als de nieuwe functie `f` die dan ontstaat nog steeds voor elke `x` differentieerbaar is?

Testen

12. Bepaal de waarden van `x` waarin de volgende functies niet differentieerbaar zijn.
    1. `f(x) = 4 - sqrt(2 - x)`
    2. `g(x) = x|x^2 - 4|`


13. Gegeven is de functie `f(x) = sqrt(4x^2 - x^3)`.
    1. Bepaal algebraïsch de nulpunten van de grafiek van `f`.
    2. Bepaal het domein van `f`.
    3. Bepaal de afgeleide van `f`.
    4. Voor welke waarden van `x` is `f` niet differentieerbaar?
    5. De lijn met vergelijking `y = kx` met `k > 0` snijdt de grafiek in precies één punt. Welke waarden kan `k` in dit geval aannemen?