De quotiëntregel

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De quotiëntregel > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De quotiëntregel > Uitleg

Lees eerst de Uitleg goed door. Probeer zelf de quotiëntregel af te leiden uit de productregel en de kettingregel.

Opgaven

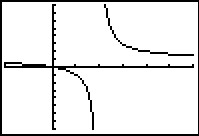  1. Je ziet hier een deel van de grafiek van de functie `f(x) = x/(x - 2)`. Deze functie is een quotiëntfunctie.
    1. Wat is de teller en wat de noemer van deze functie?
    2. In de Uitleg kun je zien hoe je deze functie kunt differentiëren met de productregel en de kettingregel. Je moet daartoe de functie eerst herschrijven. Doe dat en bepaal de afgeleide.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De quotiëntregel > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Bekijk de grafiek van de functie `f(x) = x/(x - 2)` uit de vorige opgave nog eens. Je hebt de afgeleide bepaald met behulp van de productregel en de kettingregel. In de Voorbeeld 1 zie je hoe je de quotiëntregel voor differentiëren kunt gebruiken om van dergelijke functies de afgeleide te bepalen.
    1. Bepaal de afgeleide van `f` met de quotiëntregel.
    2. De afgeleide bij opgave 1 en die bij deze opgave zouden natuurlijk hetzelfde moeten zijn. Ga na dat dit inderdaad zo is.

  2. Gegeven is de functie `f` door `f(x) = (x + 1)/(x)`.
    1. Bepaal van deze functie de afgeleide met behulp van de quotiëntregel.
    2. Je kunt ook het functievoorschrift eerst herschrijven. Dan hoef je de quotiëntregel helemaal niet te gebruiken. Bepaal nu de afgeleide zonder de quotiëntregel toe te passen. Welke van beide methodes van differentiëren is hier het handigst?

  3. Differentieer de volgende functies (met de quotiëntregel als dat nodig is, bekijk eventueel Voorbeeld 2. Probeer telkens de handigste manier van differentiëren te gebruiken.
    1. `f(x) = (3x^2 - 4)/(2x + 1)`
    2. `f(x) = 4/(x - 2)^2`
    3. `f(x) = (3x - 1)/(sqrt(4 + x^2))`
    4. `f(x) = (x^2 - 1)/(x + 1)`

  4. Gegeven is de functie `f(x) = x^3/(1 + x^4)`
    1. Bereken de extremen van `f` met behulp van differentiëren. Geef benaderingen in twee decimalen nauwkeurig.
    2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=2`.

Verwerken

  1. Differentieer de volgende functies.
    1. `f(x) = (x + 1)/(x^2 - 16x)`
    2. `y(x) = 1/(x^2 - 4x + 5)`
    3. `H(t) = sqrt(2t + 6)/(3t)`
    4. `GTK(q) = (2q^3 - 10q^2 + 60q + 120)/q`
    5. `f(x) = (2x)/(x^2 - 10)`
    6. `y(x) = (-4)/(1 - 3x^2)`
    7. `A(r) = (2r)/(sqrt(4r + 8))`
    8. `GO(p) = 200p + 400 + 2000/p`

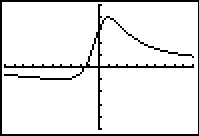  2. Je ziet hier een deel van de grafiek van functie `f`. Het functievoorschrift is `f(x) = (8x + 12)/(x^2 + 4)`.
    1. Bereken algebraïsch de uiterste waarden van `f`.
    2. Los op: `f(x) < 3/2` .
    3. De grafiek van `f` snijdt de `x`-as in `A` en de `y`-as in `B`. Laat zien, dat de lijn `AB` de grafiek van `f` raakt.

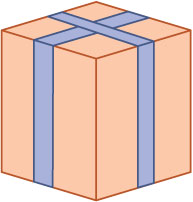  3. De afdeling Verpakking van een bedrijf heeft de opdracht gekregen balkvormige doosjes te maken waarvan de lengte vier keer zo groot is als de breedte. Om elke doos worden twee zijden sierlinten aangebracht zoals je in de tekening ziet. De inhoud van de doosjes moet 1 liter zijn. Het bedrijf wil het verbruik van het sierlint zo klein mogelijk houden.
    1. Stel een formule op voor de lengte `L` van het benodigde sierlint als functie van de breedte `x` van de doos.
    2. Bereken met behulp van differentiëren bij welke afmetingen van het doosje de lengte van het sierlint zo klein mogelijk is. Geef je antwoord in millimeter nauwkeurig.

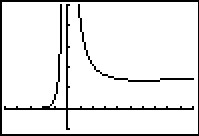  4. Hier zie je het deel van de grafiek van `f(x) = ((x + 3)^3)/(3x^2)` met `-5 <= x <= 10`.
    1. Toon aan dat `f'(x) = ((x - 6)(x + 3)^2)/(3x^3)`.
    2. Bereken het (lokale) minimum van `f`.
    3. Waarom is het punt `(-3,0)` een buigpunt van de grafiek van `f`?

  5. Een gelijkstroomcircuit bestaat uit een 12 volts batterij met een inwendige weerstand van 12 ohm en een variabele weerstand van `R` (ohm). Het vermogen `P` (in watt) dat door dit circuit wordt opgewekt, wordt gegeven door `P = RI^2`. De stroomsterkte `I` wordt daarin gegeven door `I = (12)/(R + 12)`.
    1. Druk het ontwikkelde vermogen uit in `R`, de variabele weerstand.
    2. Bereken het maximaal ontwikkelde vermogen met behulp van differentiëren.

Testen

  1. Differentieer de volgende functies.
    1. `f(x) = (2x + 5)/(1 - x)`
    2. `g(x) = (sqrt(x))/(1 + x^3)`
    3. `H(t) = 1/(1 + 1/t)`
    4. `y(x) = (x^4 + 1)/(1 + x^2)^4`

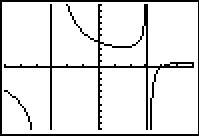  2. Je ziet hier een deel van de grafiek van de functie `f(x) = (10x - 40)/(x^2 - 10)`.
    1. Bereken met behulp van de afgeleide de extremen van `f` in twee decimalen nauwkeurig.
    2. Het punt `(0,4)` ligt op de grafiek van `f`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in dat punt.

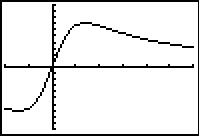  3. Dit is een deel van de grafiek van `f(x) = (10x)/(0,5x^2 + 1)`.
    1. Bereken exact de twee extremen van functie `f`.
    2. Bepaal de tweede afgeleide van `f`.
    3. Bepaal de buigpunten van de grafiek van `f`.