De productregel

Inleiding

Als je twee functievoorschriften f(x) en g(x) vermenigvuldigt, krijg je een nieuwe functie die de productfunctie van f en g heet. Vaak kun je die producten uitwerken, maar niet altijd. En soms is dit gewoon te bewerkelijk.
Daarom moet je een differentieerregel hebben voor productfuncties f(x) · g(x).

Je leert nu:

• de regel voor het differentiëren van productfuncties;
• de productregel toepassen.

Je kunt al:

• allerlei soorten functies gebruiken;
• differentiëren met de machtsregel, de constante-regel, de somregel en de kettingregel;
• werken met de afgeleide en de tweede afgeleide, onder andere voor het berekenen van extremen en buigpunten.

Verkennen

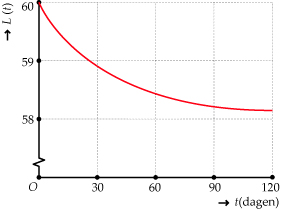
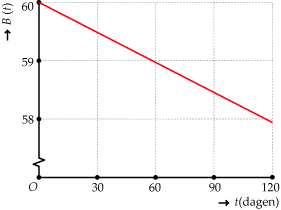
In deze grafieken zie je hoe de lengte L en de breedte B van een plank van 60 cm bij 60 cm in de loop van de tijd veranderen.

> In welke periode krimpt de plank in de lengte sneller dan in de breedte?
> Op t = 0 is de plank vierkant. Tijdens het krimpen verandert de verhouding tussen lengte en breedte. Na hoeveel dagen is de plank opnieuw ongeveer vierkant?
> Op t = 90 is de lengte van de plank 58,3 cm en de breedte van de plank 58,5 cm. De plank krimpt dan in de lengte met 0,007 cm per dag en in de breedte met 0,017 cm per dag. Met hoeveel cm per dag verandert de oppervlakte dan?

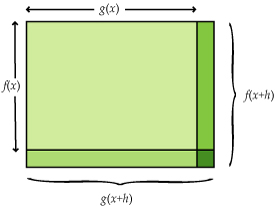
Uitleg

Als lengte en breedte van een rechthoek functies van x zijn, is de oppervlakte A een productfunctie in x: A(x) = f(x) · g(x).
Je kunt de oppervlakte van deze rechthoek variëren door x te laten toenemen tot x + h. De nieuwe oppervlakte is:
A(x + h) = f(x + h) · g(x + h) en:

$A\text{'}(x)=\underset{h\to 0}{\lim }\frac{A(x+h)-A(x)}{h}=\underset{h\to 0}{\lim }\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Met behulp van lineaire benadering van f(x + h) en g(x + h) wordt dit:
A'(x) = $\underset{h\to 0}{\lim }\frac{(f(x)+h\cdot f\text{'}(x))(g(x)+h\cdot g\text{'}(x))-f(x)\cdot g(x)}{h}$ =
        = $\underset{h\to 0}{\lim }\frac{h\cdot f\text{'}(x)\cdot g(x)+h\cdot f(x)\cdot g\text{'}(x)+h^2\cdot f\text{'}(x)\cdot g\text{'}(x)}{h}$

In de figuur is A'(x) het totaal van de drie donkerder rechthoekjes (als h naar 0).
Boven de breukstreep kun je in de drie termen de verschillende rechthoekjes herkennen.

En dus is $A\text{'}(x)=\underset{h\to 0}{\lim }\left(f\text{'}(x)\cdot g(x)+f(x)\cdot g\text{'}(x)+h\cdot f\text{'}(x)\cdot g\text{'}(x)\right)=f\text{'}(x)\cdot g(x)+f(x)\cdot g\text{'}(x)$.

Je hebt nu een manier gevonden om de afgeleide van een productfunctie te bepalen. Tenminste als f en g stijgende functies zijn met positieve functiewaarden.

Opgaven

1. Een productfunctie als `P(t)=f(t)*g(t)` kun je opvatten als de oppervlakte van een rechthoek met lengte `f(t)` en breedte `g(t)` die met de tijd `t` veranderen. (Als alle functiewaarden positief zijn.) Als je wilt kijken naar de veranderingen van die oppervlakte, dan kijk je naar het differentiequotiënt op het interval `[t,t + h]`.
   1. De toename van de oppervlakte op `[t,t + h]` is
      1. `Delta P = Delta f(t)*Delta g(t)`
      2. `Delta P = f(t)*Delta g(t)+g(t)*Delta f(t)+Delta f(t)* Delta g(t)`
      3. `Delta P = f(t)*Delta g(t)+g(t)*Delta f(t)`
   2. Uit de toename van de oppervlakte kun je een regel voor het differentiëren van `P(t)=f(t)*g(t)` afleiden. Bekijk dit in de Uitleg. Schrijf die regel op.
   3. Stel je voor dat `f(t)=t^2` en dat `g(t)=t^4`. Bepaal nu met behulp van de productregel voor differentiëren de afgeleide van de productfunctie.

Theorie

Voor de afgeleide van een product van twee functies geldt

Differentieerregel 6 (productregel):
Als P(x) = f(x) · g(x) dan is P'(x) = f'(x) · g(x) + f(x) · g'(x).

» Bewijs

Deze differentieerregel is lang niet altijd nodig, vaak kun je haakjes uitwerken.
Maar met name als je te maken krijgt met productfuncties waarbij de éne functie bijvoorbeeld een kwadratische functie is en de andere een exponentiële functie, dan is de productregel hard nodig.

Vaak komt deze regel in combinatie met de voorgaande differentieerregels voor. Vooral de kettingregel duikt daarbij nog wel eens op!

Voorbeeld 1

Differentieer de functie: P(x) = (x³ – 6x²)(x⁴ – 1).

Antwoord

Deze functie is het product van:

• f(x) = x³ – 6x² waarvoor geldt: f'(x) = 3x² – 12x
• g(x) = x⁴ – 1 waarvoor geldt: g'(x) = 4x³

P'(x) = (3x² – 12x)(x⁴ – 1) + (x³ – 6x²)(4x³)

En na haakjes uitwerken: P'(x) = 7x⁶ – 36x⁵ – 3x² + 12x.

Hier had je de productregel kunnen vermijden door direct de haakjes van functie P uit te werken.

Voorbeeld 2

Differentieer de functie: h(x) = x(2x + 1)³.

Antwoord

Deze functie is het product van:

• f(x) = x waarvoor geldt: f'(x) = 1
• g(x) = (2x + 1)³ waarvoor geldt: g'(x) = 3 · (2x + 1)² · 2 (Hierbij gebruik je de kettingregel!)

h'(x) = 1 · (2x + 1)³ + x · 3 · (2x + 1)² · 2 = (2x + 1)³ + 6x(2x + 1)².

Overigens had je ook hier eerst de haakjes van functie h uit kunnen werken en zonder productregel differentiëren.

Voorbeeld 3

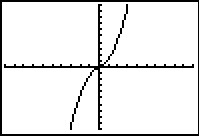
Gegeven is de functie: f(x) = $x\sqrt{1+x^2}$.
Bereken met behulp van differentiëren de hoek die de raaklijn aan de grafiek in (0, 0) met de positieve x-as maakt.

Antwoord

De afgeleide vind je met behulp van de productregel (en de kettingregel!):

$f(x)=x\cdot {\left(1+x^2\right)}^{\frac{1}{2}}$

$f\text{'}(x)=1\cdot {\left(1+x^2\right)}^{\frac{1}{2}}+x\cdot \frac{1}{2}{\left(1+x^2\right)}^{-\frac{1}{2}}\cdot 2x$

Omdat je hier alleen x = 0 moet invullen, is verder herschrijven zinloos: f'(0) = 1.

De hoek die de raaklijn aan de grafiek in (0, 0) met de x-as maakt is dus 45°.

Opgaven

2. De functie `f(x) = x^2(x^3 - 4x)` kun je opvatten als een productfunctie van `u` en `v`. Bij het differentiëren kun je dan de productregel gebruiken, zie Voorbeeld 1.
   1. Schrijf de voorschriften van `u` en `v` op.
   2. Bepaal de afgeleide van `f` met behulp van de productregel.
   3. Je kunt deze functie ook zonder de productregel differentiëren. Je moet dan eerst de haakjes uitwerken. Differentieer de functie ook op die manier.


3. Vaak heb je behalve de productregel ook de kettingregel nodig, zie Voorbeeld 2. Bijvoorbeeld bij het differentiëren van de functie `f(x) = (x^2 + 3x)(x^2 + 10)^3`.
   1. Bepaal eerst de afgeleide van `u(x) = x^2 + 3x`.
   2. Bepaal de afgeleide van `v(x)`.
   3. Bepaal nu met de productregel de afgeleide van `f`. Je hoeft de functie niet te herschrijven.


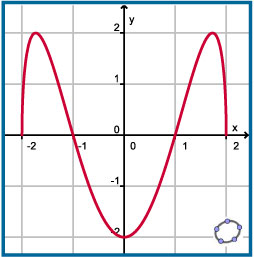4. Gegeven is de functie `f(x) = (x^2 - 1) * sqrt(4 - x^2)`. Je ziet hier de volledige grafiek van deze functie.
   1. Bepaal de afgeleide van deze functie. Bekijk eventueel Voorbeeld 3 waar een vergelijkbare functie wordt gedifferentieerd.
   2. Met behulp van deze afgeleide kun je algebraïsch de extremen van `f` berekenen. Laat zien hoe dit in zijn werk gaat.
   3. De grafiek van `f` gaat door het punt `(1,0)`. Bereken de hoek die de grafiek daar met de `x`-as maakt.

Verwerken

5. Bepaal van de volgende functies de afgeleide.
   1. `f(x) = (x^3 + 6)(4x^2 - 5x)`
   2. `g(x) = (10 - x) * sqrt(x)`
   3. `R(t) = 3t(t + 5)^4`
   4. `y(x) = x * sqrt(5 + x^2)`
   5. `y(x) = x - sqrt(5 + x^2)`
   6. `V(r) = (100 - 5/r)(20 - r)^2`


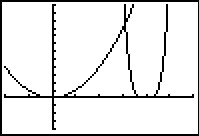6. Hier zie je de grafieken van de functies `y_1(x) = x^2` en `y_2(x) = (2x - 8)^4`. De functie `f(x) = y_1(x) * y_2(x)` is de productfunctie van beide.
   1. De nulpunten van `f` kun je uit de gegeven grafieken afleiden. Welke nulpunten heeft de grafiek van `f`?
   2. Toon aan dat `f'(x) = (2x - 8)^3(12x^2 - 16x)`
   3. Bepaal met behulp van de afgeleide de extremen van `f`.
   4. Voor welke waarden van k heeft de vergelijking `f(x)=k` precies vier oplossingen?


7. Gegeven is de functie `f(x) = 4x sqrt(x) * (1 - x)^3`.
   1. Voor welke waarden van `x` heeft de grafiek een raaklijn evenwijdig aan de `x`-as?
   2. Deze functie heeft twee extremen. Welke twee?


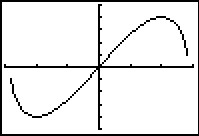8. Hier zie je de grafiek van de functie `f(x) = x * sqrt(8 - x^2)` zoals een grafische rekenmachine hem maakt.
   1. De grafiek is onvolledig. Dat kun je bijvoorbeeld zien aan de nulpunten van deze functie. Welke nulpunten heeft de grafiek van `f`?
   2. Bereken met behulp van differentiëren het bereik van `f`.
   3. De lijn met vergelijking `y=px` heeft drie punten gemeen met de grafiek van `f`. Bereken `p`.


9. Gegeven is de functie `f(x) = 0,25x^2 - x sqrt(x)`.
   1. Bereken algebraïsch het bereik van `f`.
   2. Bereken de coördinaten van het buigpunt van de grafiek van `f`.
   3. Voor welke `p` is de lijn met vergelijking `y = 2x + p` een raaklijn aan de grafiek van `f`?


10. Iemand wil met behulp van een viertal even grote rechthoekige kozijnen een serre aan zijn huis bouwen. Elk van die kozijnen is 2,5 hoog en 3 breed. Hij bestudeert eerst de mogelijke opstellingen waarbij twee kozijnen `AB` en `DE` loodrecht op de muur worden bevestigd. De andere twee `BC` en `CD` worden zo geplaatst dat de vloeroppervlakte van de serre maximaal wordt.
    
        
    
    
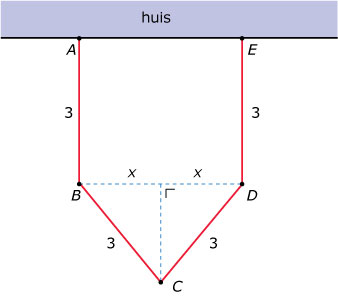
    1. De afstand tussen de twee kozijnen die loodrecht op de muur staan is `2x`. Toon aan dat voor de vloeroppervlakte `A` van de serre geldt: `A(x)=6x+x*sqrt(9-x^2)`
    2. Bereken algebraïsch de grootst mogelijke vloeroppervlakte van deze serre.

Testen

11. Bepaal de afgeleide van de volgende functies:
    1. `f(x) = 6x(1 + x^2)^3`
    2. `H(t) = t * sqrt(1 - t^2)`
    3. `y(x) = (ax - 4)^2(6 - x)^3`
    4. `g(x) = sqrt(1 + sqrt(x))`


12. Gegeven is de functie `f(x) = x^2 - 4x sqrt(x) + 4x`
1. Bepaal de nulwaarden van `f`.
2. Bereken algebraïsch de extremen van `f`.
3. Bereken algebraïsch het buigpunt van de grafiek van `f`.
4. De raaklijn `l` in de oorsprong aan de grafiek van `f` wordt `a` eenheden in de positieve `x`-richting verschoven. De nieuwe lijn `m` die daardoor ontstaat raakt ook aan de grafiek van `f`. Bereken `a`.


13. Gegeven is de functie `f(x) = (x^2 - 100)^4`. Bepaal de tweede afgeleide van deze functie.