De productregel

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De productregel > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden. De oppervlakte van een plank waarvan lengte en breedte variëren door krimpen is een voorbeeld van een productfunctie.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De productregel > Uitleg

Lees in de Uitleg wat een productfunctie is.

Opgaven

1. Een productfunctie als `P(t)=f(t)*g(t)` kun je opvatten als de oppervlakte van een rechthoek met lengte `f(t)` en breedte `g(t)` die met de tijd `t` veranderen. (Als alle functiewaarden positief zijn.) Als je wilt kijken naar de veranderingen van die oppervlakte, dan kijk je naar het differentiequotiënt op het interval `[t,t + h]`.
   1. De toename van de oppervlakte op `[t,t + h]` is
      1. `Delta P = Delta f(t)*Delta g(t)`
      2. `Delta P = f(t)*Delta g(t)+g(t)*Delta f(t)+Delta f(t)* Delta g(t)`
      3. `Delta P = f(t)*Delta g(t)+g(t)*Delta f(t)`
   2. Uit de toename van de oppervlakte kun je een regel voor het differentiëren van `P(t)=f(t)*g(t)` afleiden. Bekijk dit in de Uitleg. Schrijf die regel op.
   3. Stel je voor dat `f(t)=t^2` en dat `g(t)=t^4`. Bepaal nu met behulp van de productregel voor differentiëren de afgeleide van de productfunctie.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > De productregel > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

2. De functie `f(x) = x^2(x^3 - 4x)` kun je opvatten als een productfunctie van `u` en `v`. Bij het differentiëren kun je dan de productregel gebruiken, zie Voorbeeld 1.
   1. Schrijf de voorschriften van `u` en `v` op.
   2. Bepaal de afgeleide van `f` met behulp van de productregel.
   3. Je kunt deze functie ook zonder de productregel differentiëren. Je moet dan eerst de haakjes uitwerken. Differentieer de functie ook op die manier.


3. Vaak heb je behalve de productregel ook de kettingregel nodig, zie Voorbeeld 2. Bijvoorbeeld bij het differentiëren van de functie `f(x) = (x^2 + 3x)(x^2 + 10)^3`.
   1. Bepaal eerst de afgeleide van `u(x) = x^2 + 3x`.
   2. Bepaal de afgeleide van `v(x)`.
   3. Bepaal nu met de productregel de afgeleide van `f`. Je hoeft de functie niet te herschrijven.


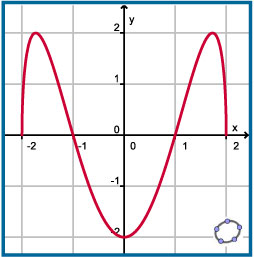4. Gegeven is de functie `f(x) = (x^2 - 1) * sqrt(4 - x^2)`. Je ziet hier de volledige grafiek van deze functie.
   1. Bepaal de afgeleide van deze functie. Bekijk eventueel Voorbeeld 3 waar een vergelijkbare functie wordt gedifferentieerd.
   2. Met behulp van deze afgeleide kun je algebraïsch de extremen van `f` berekenen. Laat zien hoe dit in zijn werk gaat.
   3. De grafiek van `f` gaat door het punt `(1,0)`. Bereken de hoek die de grafiek daar met de `x`-as maakt.

Verwerken

5. Bepaal van de volgende functies de afgeleide.
   1. `f(x) = (x^3 + 6)(4x^2 - 5x)`
   2. `g(x) = (10 - x) * sqrt(x)`
   3. `R(t) = 3t(t + 5)^4`
   4. `y(x) = x * sqrt(5 + x^2)`
   5. `y(x) = x - sqrt(5 + x^2)`
   6. `V(r) = (100 - 5/r)(20 - r)^2`


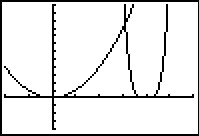6. Hier zie je de grafieken van de functies `y_1(x) = x^2` en `y_2(x) = (2x - 8)^4`. De functie `f(x) = y_1(x) * y_2(x)` is de productfunctie van beide.
   1. De nulpunten van `f` kun je uit de gegeven grafieken afleiden. Welke nulpunten heeft de grafiek van `f`?
   2. Toon aan dat `f'(x) = (2x - 8)^3(12x^2 - 16x)`
   3. Bepaal met behulp van de afgeleide de extremen van `f`.
   4. Voor welke waarden van k heeft de vergelijking `f(x)=k` precies vier oplossingen?


7. Gegeven is de functie `f(x) = 4x sqrt(x) * (1 - x)^3`.
   1. Voor welke waarden van `x` heeft de grafiek een raaklijn evenwijdig aan de `x`-as?
   2. Deze functie heeft twee extremen. Welke twee?


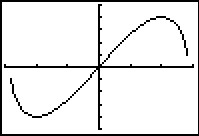8. Hier zie je de grafiek van de functie `f(x) = x * sqrt(8 - x^2)` zoals een grafische rekenmachine hem maakt.
   1. De grafiek is onvolledig. Dat kun je bijvoorbeeld zien aan de nulpunten van deze functie. Welke nulpunten heeft de grafiek van `f`?
   2. Bereken met behulp van differentiëren het bereik van `f`.
   3. De lijn met vergelijking `y=px` heeft drie punten gemeen met de grafiek van `f`. Bereken `p`.


9. Gegeven is de functie `f(x) = 0,25x^2 - x sqrt(x)`.
   1. Bereken algebraïsch het bereik van `f`.
   2. Bereken de coördinaten van het buigpunt van de grafiek van `f`.
   3. Voor welke `p` is de lijn met vergelijking `y = 2x + p` een raaklijn aan de grafiek van `f`?


10. Iemand wil met behulp van een viertal even grote rechthoekige kozijnen een serre aan zijn huis bouwen. Elk van die kozijnen is 2,5 hoog en 3 breed. Hij bestudeert eerst de mogelijke opstellingen waarbij twee kozijnen `AB` en `DE` loodrecht op de muur worden bevestigd. De andere twee `BC` en `CD` worden zo geplaatst dat de vloeroppervlakte van de serre maximaal wordt.
    
        
    
    
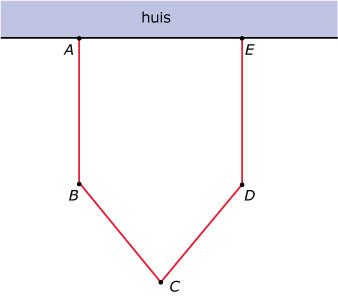
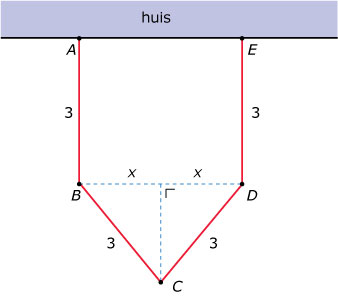
    1. De afstand tussen de twee kozijnen die loodrecht op de muur staan is `2x`. Toon aan dat voor de vloeroppervlakte `A` van de serre geldt: `A(x)=6x+x*sqrt(9-x^2)`
    2. Bereken algebraïsch de grootst mogelijke vloeroppervlakte van deze serre.

Testen

11. Bepaal de afgeleide van de volgende functies:
    1. `f(x) = 6x(1 + x^2)^3`
    2. `H(t) = t * sqrt(1 - t^2)`
    3. `y(x) = (ax - 4)^2(6 - x)^3`
    4. `g(x) = sqrt(1 + sqrt(x))`


12. Gegeven is de functie `f(x) = x^2 - 4x sqrt(x) + 4x`
1. Bepaal de nulwaarden van `f`.
2. Bereken algebraïsch de extremen van `f`.
3. Bereken algebraïsch het buigpunt van de grafiek van `f`.
4. De raaklijn `l` in de oorsprong aan de grafiek van `f` wordt `a` eenheden in de positieve `x`-richting verschoven. De nieuwe lijn `m` die daardoor ontstaat raakt ook aan de grafiek van `f`. Bereken `a`.


13. Gegeven is de functie `f(x) = (x^2 - 100)^4`. Bepaal de tweede afgeleide van deze functie.