Differentieerregels

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerregels > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerregels > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

  1. Je hebt al geleerd wat differentiëren is.
    1. Omschrijf wat differentiëren precies is.
    2. Hoe kom je aan de regels voor het differentiëren?
    3. Welke differentieerregels pas je toe bij het bepalen van de afgeleide van `f(x) = 3x^3 + 6x^2 - 12`?
    4. Kun je met behulp van differentieerregels de afgeleide bepalen van `f(x) = (2x)^3`? Zo ja, hoe?
    5. Waarom kun je met de differentieerregels die je op dit moment kent moeilijk de afgeleide bepalen van `f(x) = (2x + 3)^(12)`?
    6. Waarom kun je met de differentieerregels die je op dit moment kent wel de afgeleide bepalen van `f(x) = (2x + 3x^2)/(x)` maar niet de afgeleide bepalen van `g(x) = (2x + 3x^2)/(x + 1)`?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerregels > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. Om de afgeleide (de hellingsfunctie) van een functie te kunnen bepalen moet je differentiëren. In de Theorie vind je de differentieerregels die je daarvoor tot nu toe hebt geleerd. Functievoorschriften die niet in de juiste vorm staan moet je eerst herschrijven. Differentieer de volgende functies. Bekijk eventueel eerst Voorbeeld 1.
    1. `f(x) = 6 - 1/2 x^3`
    2. `TK(q) = 2q^3 + 60q^2 - 100q + 50`
    3. `I(d) = 1/6 pi d^3 + a^2`
    4. `f(x) = x(x - 20)(x + 30)`
    5. `f(x) = x^4 + 6x + 12`
    6. `H(t) = 25t - 5t^2`
    7. `T(p) = a^2p^3 - ap + a^4`
    8. `f(x) = x(x + 4)^2`

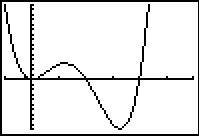  2. Bekijk de grafiek van de functie `f` met voorschrift `f(x) = x^2(x - 20)(x - 40)`.
    1. Om zelf de grafiek zo in beeld te krijgen, bepaal je eerst algebraïsch de nulpunten van de functie. Vervolgens kijk je naar de tabel en stel je het venster van je grafische rekenmachine in. Welke instellingen geven (ongeveer) hetzelfde deel van de grafiek te zien?
    2. Wil je de extremen van `f` algebraïsch berekenen, dan moet je eerst de functie differentiëren. In Voorbeeld 2 zie je hoe dat bij een dergelijke functie gaat. Je moet eerst de haakjes uitwerken. Doe dat en bepaal vervolgens de afgeleide.
    3. Bereken nu de extremen van `f` in gehelen nauwkeurig.
    4. Op grond van de grafiek lijken er twee buigpunten te zijn. Met behulp van de tweede afgeleide kun je die bepalen. Bereken ook die buigpunten algebraïsch in gehelen nauwkeurig.

  3. Bekijk de grafiek van de functie `f` met voorschrift `f(x) = x^2(x - 20)(x - 40)` uit de vorige opgave.
    1. Het punt `(20,0)` is een nulpunt van de grafiek van `f`. De raaklijn aan die grafiek maakt daar een hoek `alpha` met de `x`-as. Zie eventueel Voorbeeld 3. Bereken de grootte van die hoek in hondersten van graden nauwkeurig.
    2. Waarom zal in de grafiek die hoek waarschijnlijk anders zijn?
    3. Er zijn nog andere punten op de grafiek van `f` waarin de raaklijn dezelfde hoek maakt met de `x`-as. Bereken de `x`-waarden van die punten in één decimaal nauwkeurig.

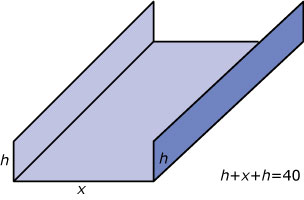  4. Een Nederlands bedrijf maakt goten voor bevloeiing van akkers in een ontwikkelingsland. Die goten worden gemaakt door vlakke platen kunststof te buigen. Die platen zijn 2 meter lang en 40 centimeter breed. Ze worden zo gebogen dat een goot ontstaat van 2 meter lang met als dwarsdoorsnede (in de breedterichting) een rechthoek.
    1. De breedte van de goot noem je `x` en de hoogte is `h`. Welke verband bestaat er tussen `x` en `h`? Stel een formule voor dat verband op.
    2. Je kunt nu een formule opstellen voor de hoeveelheid water die zo’n goot kan bevatten. Druk de hoeveelheid water `H` in uit in `x`.
    3. Bereken bij welke waarde van `x` die hoeveelheid water maximaal is.

Verwerken

  1. Differentieer de volgende functies.
    1. `f(x) = 5x^6 - 13x^5 + 10x - 25`
    2. `f(x) = ax^2 + bx + c`
    3. `P(I) = RI^2`
    4. `y(x) = (x^2 - 1)(x^2 - 9)`
    5. `f(x) = -8x^8 - 88`
    6. `f(x) = 2ax^3 - 3a^2x + a^3`
    7. `A(r) = pi r^2 + l2r`
    8. `h(x) = 3x^2(10 - x)^2`

  2. Gegeven is de functie `f(x) = 4/5x^3 - 3x^2`.
    1. Bereken algebraïsch de extremen van `f`.
    2. Bereken algebraïsch de coördinaten van het buigpunt van de grafiek van `f`.

  3. Het punt `(2,0)` ligt op de grafiek van de functie `y = x^3 - 5x^2 + 7x - 2`.
    1. Bereken de hoek die de raaklijn in dit punt aan de grafiek maakt met de `x`-as.
    2. In hoeveel andere punten van de grafiek maakt de raaklijn dezelfde hoek met de `x`-as?

  4. Uit een stuk karton van 20 bij 60 centimeter wordt een bakje gevouwen. Neem voor de hoogte van dit bakje `x` cm.



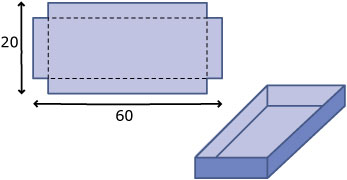
    1. De inhoud `I` van dit bakje hangt alleen af van `x` (als er verder niets boven het open bovenvlak mag uitsteken). Stel een bijpassend functievoorschrift `I(x)` op.
    2. Bereken algebraïsch bij welke waarde van `x` de inhoud van het bakje maximaal is.

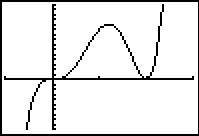  5. Hier zie je een deel van de grafiek van `f(x) = x^3(x - 20)^2`.
    1. In het deel van de grafiek dat in beeld is, bevinden zich drie punten waarin de raaklijn aan de grafiek evenwijdig is aan de `x`-as. Bereken de `x`-coördinaten van die drie punten algebraïsch.
    2. Waarom heeft de functie `f` toch maar twee (lokale) extremen?
    3. Laat zien dat de grafiek van `f` wel drie buigpunten heeft.

Testen

  1. Differentieer de volgende functies:
    1. `f(x) = -0,5x^4 + 3x`
    2. `f(x) = 10 - 6x^2 - x^4`
    3. `f(x) = (x - 1)(x^2 - 1)`
    4. `f(x) = ax(1 - x^2)`
    5. `H(t) = 3p^2 + 4pt^3`
    6. `y(t) = 20t^2(10 - t)(15 + t)`

  2. Het punt `(2,7)` ligt op de grafiek van `f(x) = 1/24x^4 + 1/6x^3 + 1/2x^2 + x + 1`.
    1. Controleer deze bewering met een berekening.
    2. Bereken de richtingscoëfficiënt van de raaklijn aan de grafiek van `f` in het punt `(2,7)`.
    3. Bereken de hoek waaronder de grafiek van `f` de `y`-as snijdt.

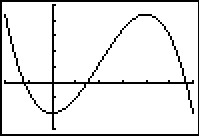  3. Je ziet hier een deel van de grafiek van de functie `y = -x^3 + 6x^2 - 10`.
    1. De grafiek heeft twee (lokale) extremen. Bereken beide extremen.
    2. Bereken het buigpunt van de grafiek.