
Veeltermen
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Uitleg
Lees eerst de Uitleg goed door.
Opgaven
-
In de Uitleg zie wat een veeltermfunctie is en hoe je er toppen en buigpunten van berekent.
- Bepaal de `x`-waarden van de toppen door de vergelijking `f'(x) = 8x^7 - 60x^5 + 140x^3 - 100x = 0` met de GR op te lossen.
- Bepaal de `x`-waarden van de buigpunten door de vergelijking `f''(x) = 56x^6 - 300x^4 + 420x^2 - 100 = 0` met de GR op te lossen.
- Kun je je voorstellen wat de hoofdstelling van de algebra inhoudt?
-
Neem `f(x) = (x^2 - 1)(x^2 - 2)`.
-
Bereken algebraïsch de nulpunten van de grafiek van `f`.
-
Bereken algebraïsch de extremen van `f`.
-
Bereken algebraïsch de buigpunten van de grafiek van `f`.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
In Voorbeeld 1 zie je hoe je van een veeltermfunctie de nulpunten, de extremen en de buigpunten kunt berekenen.
Je ziet hier de grafieken van `f(x) = x^3 - 5x^2 + 5x - 1` en `g(x) = 1 - x^4`.
Uit de figuur kun je aflezen, dat `(1,0)` een nulpunt van de grafiek van `f` en ook een snijpunt van de grafieken van `f` en `g` lijkt te zijn.
-
Ga na dat dit klopt door `x=1` in beide functievoorschriften in te vullen.
-
Bereken algebraïsch alle nulpunten van de grafiek van `f`.
-
Bereken algebraïsch de extremen van `f`.
-
Bereken algebraïsch het buigpunt van de grafiek van `f`.
-
Los op: `f(x) <= g(x)`.
-
Los de volgende vergelijkingen algebraïsch op:
-
`x^3 - 4x^2 = 12x`
-
`-0,1x^5 = 4x^2`
-
`(x - 1)(x + 1)(2x - 5) = 5`
-
`x^3 - 4x^2 + 2x - 8 = 0`
 Bestudeer Voorbeeld 2.
Bestudeer Voorbeeld 2.
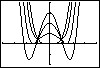
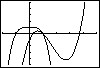
Je ziet hier een paar grafieken van functies van de vorm `f_c(x) = 1/2x^4 - cx^2 + c` op domein `[-4,4]`.
-
Bewijs dat elke functie `f_c` een extreme waarde heeft voor `x = 0`.
-
Voor welke waarden van `c` raakt de grafiek van `f_c` de `x`-as?
-
Voor welke waarden van `c` liggen de buigpunten van de grafiek van `f_c` op de `x`-as?
-
Voor welke waarden van `c` heeft de grafiek van `f_c` voor `x = 1` een hellingsgetal van `1`?
-
Gegeven zijn de functies `f(x) = x^2` en `g(x) = 2x - 8`.
Bekijk de functie `P(x) = f(x) * g(x)`. Zie ook Voorbeeld 3.
-
Bereken algebraïsch de nulpunten en de toppen van `P`.
-
Los op: `P(x) = 2x - 8`. Is het uitwerken van de haakjes hierbij nodig?
-
Los op: `P(x) <= -2x^2`.
-
Gegeven zijn de functies `f(x) = x^2` en `g(x) = 2x - 8`.
Bekijk de functie `Q(x) = f(x) // g(x)`. Zie ook Voorbeeld 4.
-
Bepaal het domein van `Q`. Waarom is `Q` geen veeltermfunctie?
-
Welke verticale asymptoot heeft de grafiek van `Q`? Welke horizontale asymptoot heeft de grafiek van `Q`?
-
Bepaal het bereik van `Q` met behulp van de grafische rekenmachine.
Verwerken
Opgaven
-
Gegeven is de derdegraadsfunctie `f` met voorschrift `f(x) = x^3 + 9x^2 - 15x + 5`.
- Breng de grafiek van `f` in beeld op je grafische rekenmachine. Welke nulpunten kun je aflezen?
-
Bereken algebraïsch de andere twee nulpunten in twee decimalen nauwkeurig.
Controleer je antwoorden met je rekenmachine.
- Bereken ook algebraïsch de toppen en het buigpunt van `f` in twee decimalen nauwkeurig.
- In welke punten van de grafiek van `f` heeft de raaklijn een richtingscoëfficiënt van `-5`?
- Welk hellingsgetal heeft de grafiek van `f` in het snijpunt met de `y`-as?
-
Los de volgende vergelijkingen algebraïsch op:
-
`x^2(x - 2) = 3x - 6`
-
`0,5x^4 + 4x^3 - 6x = 48`
-
`0,25x^6 = 4x^3 - 15`
-
`x^3 - x^2 - 2x + 2 = 0`
-
Gegeven is de familie van functies `f_p` door het voorschrift `f_p(x) = px^4 - 2x^2 + 8p`.
- Bepaal algebraïsch de nulpunten, de toppen en de buigpunten van de grafiek van `f_1`.
- Voor welke waarden van `p` raakt de grafiek van `f_p` de `x`-as?
- Voor welke waarden van `p` liggen de buigpunten van de grafiek van `f_p` op de `x`-as?
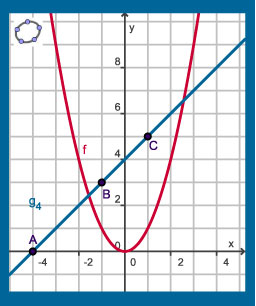 Gegeven zijn de functies `f(x) = x^2` en `g_a(x) = x + a`. In de figuur zie je de grafieken van `f` en `g_4`.
Functie `h_a` is gegeven door `h_a = f (x) * g_a(x)`.
Gegeven zijn de functies `f(x) = x^2` en `g_a(x) = x + a`. In de figuur zie je de grafieken van `f` en `g_4`.
Functie `h_a` is gegeven door `h_a = f (x) * g_a(x)`.
- Beredeneer dat de grafiek van `h_4` door de punten `O`, `A`, `B` en `C` moet gaan.
- Bereken de uiterste waarden van `h_4`.
- De snijpunten van de grafieken van `h_a` en `g_a` liggen op drie rechte lijnen. Welke?
- Bewijs dat de toppen van de grafieken van `h_a` op de kromme lijn met vergelijking `y = -1/2 x^2` liggen.
-
Gegeven zijn de functies `f_c` door `f_c(x) = cx(x + 6)^2`.
Bekijk de grafieken van deze familie van functies op het domein `[-8,1]`.
- Bereken algebraïsch de extremen van `f_1` op dit domein.
-
Alle functies `f_c` hebben een extreme waarde voor `-6 < x < 0`.
Voor welke waarden van `c` is die extreme waarde gelijk aan `80`?
- Druk de coördinaten van de buigpunten van de grafiek van `f_c` uit in `c`.
-
Voor welke waarde van `c` gaat de raaklijn aan de grafiek van `f_c` in het buigpunt door het het punt `(0,80)`?
-
Gegeven is de functie `f(x) = (10x - 40)/(x^2 - 10)`.
Bekijk de grafiek van `f` op de rekenmachine, voor `-10 <= x <= 10`.
-
Welke drie asymptoten heeft de grafiek van `f`?
Leg uit hoe deze asymptoten uit het functievoorschrift zijn af te leiden.
-
Bepaal het bereik van `f` in één decimaal nauwkeurig.
-
Voor welke waarden van `p` heeft de vergelijking `f(x) = p` precies twee oplossingen?
-
De lijn `y = 10x - 40` snijdt de grafiek van `f` van links naar rechts in drie punten `A`, `B` en `C`.
Welke van de drie lijnstukken `OA`, `OB` of `OC` is het langst?
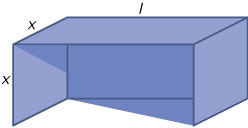 Voor het bouwen van een eenvoudige fietsenstalling is 40 m2 golfplaat beschikbaar.
Daarmee worden beide zijwanden, de achterwand en de bovenkant bekleed.
Het geraamte van het bouwsel wordt zo gemaakt dat een zuiver rechthoekig blok ontstaat, dat even hoog als diep is.
Voor het bouwen van een eenvoudige fietsenstalling is 40 m2 golfplaat beschikbaar.
Daarmee worden beide zijwanden, de achterwand en de bovenkant bekleed.
Het geraamte van het bouwsel wordt zo gemaakt dat een zuiver rechthoekig blok ontstaat, dat even hoog als diep is.
-
Druk `l` uit in `x` en leid zo een formule af voor de inhoud van het rechthoekige blok als functie van `x`.
-
Welke waarden kan `x` aannemen?
-
Welke waarden kan de inhoud van de fietsenstalling aannemen?
Testen
-
Gegeven zijn de functies `f(x) = x^4 - 6x^2 + 8` en `g(x) = -2x^2 + 20`.
- Bereken algebraïsch de nulpunten en extremen van de functie `f`.
- Bereken algebraïsch de snijpunten van de grafieken van `f` en `g`.
- Los op: `f(x) < g(x)`.
- Onderzoek hoeveel waarden voor `x` er zijn waarvoor beide grafieken dezelfde helling hebben.
-
Los op: `0,5x^3 + 2x^2 - 3x = 6`.
-
Gegeven is voor elke reële waarde van `p` de functie `f_p(x) = x^4 - 4x^3 + px^2` met het domein `RR`.
-
Bereken de nulpunten, de toppen en de buigpunten van de grafiek van `f_4`.
-
De lijn `y = mx` en de grafiek van `f_4` hebben precies drie punten gemeenschappelijk.
Bereken `m`.
-
Voor welke waarden van `p` heeft `f_p` precies drie extremen?
-
Op het domein `[-1,3]` zijn de volgende functies gegeven: `f(x) = (x - 2)^2(2x + 1)` en `g_a(x) = a(2x + 1)`.
-
Los op: `f(x) = g_2(x)`.
-
Bereken algebraïsch de nulpunten, de toppen en het buigpunt van de grafiek van `f`.
-
Voor welke waarden van `a` heeft de vergelijking `f(x) = g_a(x)` twee oplossingen?
-
Er zijn waarden van `a` waarvoor geldt dat een aantal lijnen, evenwijdig aan de grafiek van `g_a`, de grafiek van `f` raken.
Voor welke waarden van `a` is dat niet het geval?

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Veeltermen > Theorie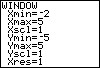
 Bestudeer Voorbeeld 2.
Bestudeer Voorbeeld 2. Gegeven zijn de functies `f(x) = x^2` en `g_a(x) = x + a`. In de figuur zie je de grafieken van `f` en `g_4`.
Functie `h_a` is gegeven door `h_a = f (x) * g_a(x)`.
Gegeven zijn de functies `f(x) = x^2` en `g_a(x) = x + a`. In de figuur zie je de grafieken van `f` en `g_4`.
Functie `h_a` is gegeven door `h_a = f (x) * g_a(x)`.
 Voor het bouwen van een eenvoudige fietsenstalling is 40 m2 golfplaat beschikbaar.
Daarmee worden beide zijwanden, de achterwand en de bovenkant bekleed.
Het geraamte van het bouwsel wordt zo gemaakt dat een zuiver rechthoekig blok ontstaat, dat even hoog als diep is.
Voor het bouwen van een eenvoudige fietsenstalling is 40 m2 golfplaat beschikbaar.
Daarmee worden beide zijwanden, de achterwand en de bovenkant bekleed.
Het geraamte van het bouwsel wordt zo gemaakt dat een zuiver rechthoekig blok ontstaat, dat even hoog als diep is.