Transformaties en differentiëren

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Transformaties en differentiëren > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Transformaties en differentiëren > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

1. Voer de in de Uitleg beschreven transformaties op de grafiek van `f(x) = -x^3 + 4x` en zijn afgeleide uit. Ga na, dat je de resultaten vindt die daar zijn aangegeven.
   


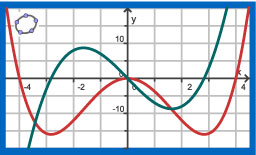2. In de figuur hiernaast zie je de grafiek van de functie `f(x) = 0,25x^4 - 4x^2` samen met zijn hellingsgrafiek, de grafiek van zijn afgeleide.
   1. Maak de grafieken van `f` en `g_1(x)=f(x)+2` met de grafische rekenmachine. De afgeleide van `g_1 `is
      1. `g_1'(x) = f'(x)`
      2. `g_1'(x) = f'(x)+2`
   2. Maak de grafieken van `f` en `g_2(x)=2*f(x)` met de grafische rekenmachine. De afgeleide van `g_2` is
      1. `g_2'(x) = f'(x)`
      2. `g_2'(x) = 2*(f'(x))`
   3. Maak de grafieken van `f` en `g_3(x)=f(x+2)` met de grafische rekenmachine. De afgeleide van `g_3` is
      1. `g_3'(x) = f'(x)`
      2. `g_3'(x) = f'(x+2)`
   4. Maak de grafieken van `f` en `g_4(x)=f(2*x)` met de grafische rekenmachine. De afgeleide van `g_4` is
      1. `g_4'(x) = f'(2*x)`
      2. `g_4'(x) = 2*(f'(2*x))`
   5. Experimenteer met andere functies, en andere verschuivingen en vermenigvuldigingen. Ga na of je de differentieerregels voor transformaties van functies zoals die in de theorie staan zelf kunt vinden.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Afgeleide functies > Transformaties en differentiëren > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. De afgeleide van `f(x) = x^4` is `f'(x) = 4x^3`. Van alle functies die door transformatie uit `f` kunnen ontstaan, kun je hiermee de afgeleide bepalen. Zie Voorbeeld 1.
   1. Bepaal de afgeleide van `g(x) = (2x)^4`
   2. Bepaal de afgeleide van `h(x) = 3(2x)^4+1`
   3. Bepaal de afgeleide van `k(x) = 5 + 2(6 - 2x)^4`


4. Gegeven is de functie `f(x) = 5(x - 1)^3 + 4.`
   1. De grafiek van `f` is door transformatie te herleiden uit die van `g(x) = x^3`. Welke transformaties moet je dan toepassen?
      1. Verschuiven in de positieve `x`-richting met 1 eenheid, dan verschuiven met 4 eenheden in de `y`-richting en tenslotte vermenigvuldigen in de `y`-richting met factor 5.
      2. Verschuiven in de negatieve `x`-richting met 1 eenheid, dan vermenigvuldigen in de `y`-richting met factor 5 en tenslotte verschuiven met 4 eenheden in de `y`-richting.
      3. Verschuiven in de positieve `x`-richting met 1 eenheid, dan vermenigvuldigen in de `y`-richting met factor 5 en tenslotte verschuiven met 4 eenheden in de `y`-richting.
   2. Je weet dat `g(1)=3`. Bereken `f'(2)`. (Zie eventueel Voorbeeld 2.)


5. De grafiek van de functie `f(x) = 8^x` kun je maken door de grafiek van `g(x) = 2^x` te vermenigvuldigen in de `x`-richting.
   1. Laat zien, dat `f(x) = g(3x)`.
   2. De vergelijking van de raaklijn aan de grafiek van `g` voor `x=0` is bij benadering `y = 0,69x + 1`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=0`.


6. Gegeven is de functie `f(x) = x^3 - 4x`.
   1. Bereken de richtingscoëfficiënt van de raaklijn aan de grafiek van `f` voor `x=1`.
   2. Met behulp van dit hellingsgetal kun je de functiewaarden in de buurt van `x=1` schatten. Ze zijn ongeveer gelijk aan de `y`-waarden van de raaklijn aan de grafiek. Bekijk eventueel Voorbeeld 3. Benader `f(1,003)`.
   3. Benader op dezelfde wijze `f(0,98)`.

Verwerken

7. De volgende functies kunnen ontstaan door transformatie van een bijpassende basisfunctie. Bedenk telkens welke basisfunctie dat is en bepaal dan de juiste afgeleide.
   1. `y = 5x^4`
   2. `y = 6(2x + 3)^4`
   3. `f(x) = (x + 2)^5 - 100`
   4. `y(t) = (2t + 4)^3`
   5. `h(t) = 1 - 2(6 - 3t)^4`
   6. `s(t) = 12(t - 10) + 2(t - 10)^2`


8. Van een functie `f` is het voorschrift niet bekend. De grafiek van `f` gaat door het punt `(1,6)`. De raaklijn aan de grafiek van `f` in dit punt heeft de vergelijking `y = 4x + 2`. De grafiek van de functie `g(x) = 3f(x) + 2` gaat door het punt `(1,20)`.
   Stel een vergelijking op van de raaklijn aan de grafiek van `g` in dit punt.
   


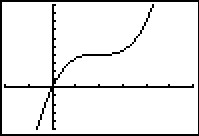9. Breng de grafiek van de functie `f(x) = 0,5(x - 2)^3 + 4` met je grafische rekenmachine zo in beeld als je hier ziet.
   1. De grafiek heeft een symmetriepunt. Welk punt is dat?
   2. Laat met behulp van de afgeleide zien waarom dit een symmetriepunt is.
   3. Stel een vergelijking op van de raaklijn in het nulpunt van de grafiek van `f`.


10. De grafiek van de functie `f(x) = (1/2)^x + 4` kun je maken door de grafiek van `g(x) = 2^x` eerst te vermenigvuldigen in de `x`-richting en dan 4 eenheden te verschuiven in de positieve `y`-richting.
    1. Met welke factor moet je de grafiek van `g` vermenigvuldigen?
    2. De vergelijking van de raaklijn aan de grafiek van `g` voor `x = 1` is ongeveer `y = 1,38x + 0,62`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = -1`.
    3. Waarom kun je `f'(1)` niet vinden met behulp van `g'(1)`?


11. Gegeven is een functie `f(x)` met `f'(1) = 2,75`.
    Bereken `g'(1)` als `g(x) = f(3x - 2)`.
    


12. Van een functie `f` is gegeven dat `f(10) = 350` en `f'(10) = -12`.
    Bepaal een lineaire benadering van `f(10,3)`.
    

Testen

13. Differentieer de volgende functies
    1. `f(x) = (3x + 6)^5 - 20`
    2. `g(x) = 16 - 2(x - 1)^4`
    3. `K(q) = 200 + (60 + 3q)^3`


14. Gegeven is de functie `f(x) = a(x - b)^5` met `a != 0` en `b != 0`.
    1. Hoe kun je de grafiek van `f` door transformatie laten ontstaan uit die van `y=x^4`?
       1. Verschuiven in de `x`-richting met `b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `a`.
       2. Verschuiven in de `x`-richting met `-b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `a`.
       3. Verschuiven in de `x`-richting met `b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `1/a`.
       4. Verschuiven in de `x`-richting met `-b` eenheden en vervolgens vermenigvuldigen in de `y`-richting met factor `1/a`.
    2. Druk `f'(2)` uit in `a` en `b`.


15. De grafiek van de functie `g(x) = (1/3)^x + 5` kan door transformatie ontstaan uit die van `f(x) = 3^x`.
    1. Welke transformaties moet je dan toepassen?
       1. Eerst vermenigvuldigen met `1/3` in de `x`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
       2. Eerst vermenigvuldigen met `-1` in de `x`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
       3. Eerst vermenigvuldigen met `-1` in de `y`-richting en dan de grafiek `5` eenheden in de positieve `y`-richting verschuiven.
    2. De raaklijn aan de grafiek van `f` voor `x = 0` heeft de vergelijking `y = 1,1x + 1`. Stel een vergelijking op van de raaklijn aan de grafiek van `g` voor dezelfde waarde van `x`.


16. De slingertijd van de slinger van een klok wordt gegeven door `T = 2pi * sqrt(l/g)` waarin `T` de slingertijd in seconden en `l` de lengte van de slinger in meter is. De constante `g` noem je de gravitatieconstante en is ongeveer `9,8` m/s².
    1. Een bepaalde klok loopt goed als zijn slingertijd 1 seconde bedraagt. Hoe lang moet de slinger dan zijn?
    2. Benader met je grafische rekenmachine `T'(l)` voor de bij a berekende lengte van de slinger.
    3. De lengte van de slinger neemt door uitzetting met 1% toe. Schat met een lineaire benadering met hoeveel seconden de slingertijd toeneemt.