
Normaal of niet?
Antwoorden bij de opgaven
-
-
Als het goed is krijg je een rechte lijn die bij 70,125 op 50% zit.
-
Ja.
-
Bij 50% kun je `mu` aflezen en bij `84%` kun je `mu + sigma` aflezen (vuistregels).
| gewicht | cum.rel.freq. |
| |
| 35-< 40 | 0,010 |
| 40-< 45 | 0,025 |
| 45-< 50 | 0,050 |
| 50-< 55 | 0,125 |
| 55-< 60 | 0,200 |
| 60-< 65 | 0,325 |
| 65-< 70 | 0,475 |
| 70-< 75 | 0,650 |
| 75-< 80 | 0,800 |
| 80-< 85 | 0,900 |
| 85-< 90 | 0,950 |
| 90-< 95 | 0,975 |
| 95-<100 | 0,990 |
| 100-<105 | 1,000 |
-
-
Zie tabel.
-
Doen.
-
Verschillen zijn niet erg groot. Je moet de bovengrenzen van de klassen gebruiken omdat het om "kleiner of gelijk" kansen gaat.
-
Ja.
-
-
-
-
-
-
-
-
-
-
Controleren door zelf aflezen.
-
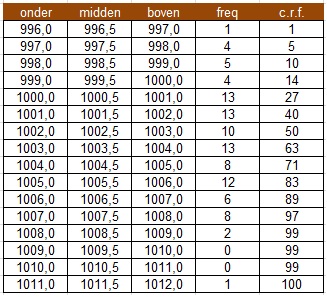
Gebruik de gegevens van machine 1 en werk met Excel.
Hiernaast zie je de tabel met cumulatieve relatieve frequenties (c.r.f.).
-
`mu ~~ 1003,1` en `sigma ~~ 3,0` gram.
-
Gebruik de bovengrenzen van elke klasse!
-
Klopt redelijk, er kan redelijk goed een rechte lijn door de punten worden getekend.
-
Aflezen uit je figuur.
-
Aflezen bij 90% geeft ongeveer 1007 gram, dus 1007 gram of meer.
-
-
Zie voorbeeld.
-
Doen.
-
`V` is de diameter van een moer min de diameter van de bijbehorende bout.
`text(P)(V < 0 | mu = 0,05 text( en ) sigma ~~ 0,058) ~~ 0,1943`, dus ongeveer 19% van de bouten is te dik.
-
`text(P)(V < 0,02 | mu = 0,05 text( en ) sigma ~~ 0,058) ~~ 0,3025`, dus ongeveer 30% van de bouten past niet.
-
`G` is het totale gewicht van een bout en de bijbehorende moer. `mu(G) = 12,3` gram en `sigma(G) = sqrt(0,2^2 + 0,3^2) ~~ 0,36` gram.
Het gewicht van 100 bouten en moeren bedraagt gemiddeld 1230 gram met een standaardafwijking van `sqrt(100) * 0,36 = 3,6` gram.
-
`text(P)(G > 1235 | mu = 1230 text( en ) sigma ~~ 3,6) ~~ 0,0824`, dus ongeveer 8% van de dozen.
-
-
Mannen: `mu ~~ 128,5` en `sigma ~~ 12,6`.
Vrouwen: `mu ~~ 131,7` en `sigma ~~ 13,7`.
-
Klassenbreedte 5 en eerste klasse `102,5 -< 107,5`.
-
Er komt niet ongeveer een rechte lijn.
-
Je kunt altijd wel een rechte lijn door een verzameling punten tekenen, maar de afwijkingen zullen vrij groot zijn.
-
Nee, ook niet. Beide verdelingen zijn behoorlijk scheef.
-
-
De gemiddelde lengte is 162 cm en de standaarddeviatie is 6,5 cm.
-
-
-
Ja, de lichaamslengte van deze 5001 vrouwen is redelijk goed normaal verdeeld.
-
Ongeveer tussen 149 en 175 cm. Dus `a ~~ 13` cm.
-
Ongeveer 169 cm of groter.
-
-
Gemiddelde gewicht 10270 gram met een standaardafwijking van `sqrt((sqrt(50) * 4)^2 + 5,5^2) ~~ 28,8` gram.
-
`text(P)(G < 10250 | mu = 10270 text( en ) sigma ~~ 28,8) ~~ 0,2437`, dus ongeveer 24% van de dozen.
-
-
`mu ~~ 43,6` en `sigma ~~ 2,7` cm.
-
-
-
Ja, de kniehoogte van deze 5001 vrouwen is redelijk goed normaal verdeeld.
-
Tussen 41,3 en 45,9 cm. Dus `a ~~ 2,3` cm.
-
46,4 cm of meer.
-
-
`text(P)(l < 60 | mu = m text( en ) sigma = s) = 0,875` geeft `(60 - m)/s ~~ 1,15`.
`text(P)(l < 30 | mu = m text( en ) sigma = s) = 0,39` geeft `(30 - m)/s ~~ -0,28`.
Dus: `60 - m = 1,15s` en `30 - m = -0,28s`. Hieruit vind je `m ~~ 39,5` en `s ~~ 21,0`. Dus `mu ~~ 39,5` en `sigma ~~ 21,0`.
-
`text(P)(l < g | mu = 35,9 text( en ) sigma = 21,0) = 0,30` geeft `g ~~ 24,9`. Dus tot een lengte van ongeveer 25 cm moeten de planten worden vernietigd.
-
-
`sigma ~~ 60,8` gram
-
4,8%
-
1006,9 gram (ofwel 1007 gram)
-
`text(P)(g < 1000 | mu = m text( en ) sigma = 7) = 0,15` geeft `mu ~~ 1007`.
-
`text(P)(g < 1000 | mu = 1015 text( en ) sigma = s) = 0,015` geeft `sigma ~~ 6,91`.
-
-
Ongeveer 4,78% (ofwel 5%).
-
Buiten het gebied van 29,76 t/m 32,24 zit 3,88% (ofwel 4%).
-
Onder de 30 gram zit 4,78% (ofwel 5%).
-
Ongeveer 31,3958 gram, ofwel 31,4 gram.
-
-
`V` is het normaal verdeelde verschil tussen het volume van het pak en het vulvolume in mL.
`text(P)(V < 0 | mu = 5 text( en ) sigma ~~ 7,2) ~~ 0,2437` dus in ongeveer 24% van de gevallen.
-
`text(P)(V < 0 | mu = m text( en ) sigma ~~ 7,2) <= 0,01` geeft `m = mu(V) ~~ 16,8`.
Omdat het gemiddelde volume van een pak 1010 mL bedraagt moet het gemiddelde vulvolume dan 1003,2 mL zijn.

