
Normaalkromme
Antwoorden bij de opgaven
-
-
Doen, zie voorbeeld 1.
-
`0,16 + 0,19 + 0,19 = 0,54`
-
`T` is een continue stochast omdat de tijd vloeiend verloopt, alle waarden vanaf 0 tot heel groot (in de praktijk tot aan 12) kan aannemen.
-
Je schatting zal weinig verschillen van het antwoord bij b.
-
Omdat je bij een continue variabele rekening moet houden met afrondingen en alle waarden tot 3,5 op 3 worden afgerond.
-
-
`text(P)(2,5 <= T < 3,5) ~~ 0,17`
-
`text(P)(T >= 2,5) ~~ 0,55`
-
100%
-
-
`L` kan alle waarden aannemen vanaf ongeveer 100 cm tot ongeveer 250 cm.
-
De meeste mensen zitten in de buurt van het gemiddelde, maar weinig mensen zijn veel groter of veel kleiner.
Gaat de grafiek over mannen en vrouwen, dan kunnen er wel twee toppen ontstaan omdat mannen gemiddeld groter zijn dan vrouwen.
Maar bij soldaten gaat het in de meeste landen alleen om mannen.
-
Omdat 182 precies het gemiddelde is en de grafiek in twee gelijke delen verdeelt.
-
Ongeveer `0,1 + 0,7 + 3,4 + 11,6 + 4/5 * 23,8 ~~ 35`%.
-
100%
-
-
`179,5 - < 180,5` en daar zit 5,5% van de soldaten in.
-
`0,013 + 0,017 + 0,021 + 0,025 + 0,030 + 0,035 = 0,141` dus 14,1%.
-
Dat zou ongeveer 68% moeten zijn.
-
Ongeveer 6,6%.
-
`0,022 + 0,027 + 0,034 + 0,040 + 0,047 + 0,053 = 0,223` dus 22,3%.
-
Dat moet weer ongeveer 68% zijn.
-
Het betreft de eerste vuistregel.
-
-
De transactietijd zal in het algemeen niet symmetrisch verdeeld zijn. Veel transacties kunnen snel worden afgehandeld, maar heel weinig duren erg lang.
-
-
-
Vrijwel 0.
-
-
-
-
`17,8 + 12,2 = 30,0`%.
-
`20,7 + 14,1 = 34,8`%.
-
Redelijk, het is geen perfecte normale verdeling.
-
-
-
-
-
-
95 %.
-
Redelijk, het is geen perfecte normale verdeling.
-
-
Bijna 100%.
-
-
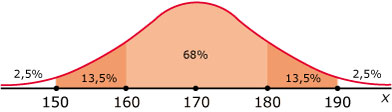
I 2,5%, II 13,5%, III 34%, IV 34%, V 13,5%, VI 2,5%.
-
16%
-
81,5%
-
84%
-
-
-
-
68% + 16% = 84%
-
68% + 13,5% = 81,5%
-
84%
-
-
Normaal verdeeld.
-
Normaal verdeeld.
-
Waarschijnlijk niet normaal verdeeld, het gewicht is sterk te beïnvloeden door (slechte) eetgewoontes.
-
Normaal verdeeld, wellicht afhankelijk van de manier waarop die reactietijd wordt getest.
-
Niet normaal verdeeld, er zijn veel meer lagere inkomens dan top inkomens, de verdeling is erg scheef.
-
Niet normaal verdeeld, kleinere wachttijden zullen vaker voorkomen dan grotere.
-
-
Er ontstaat geen heel mooie symmetrische klokvorm, maar vooruit...
-
`mu ~~ 1005` en `sigma ~~ 2,4` gram.
-
Volgens het histogram 6%.
-
1000 gram is ongeveer het gemiddelde min 2 keer de standaardafwijking. Daar zou 2,5% onder moeten zitten volgens de vuistregels.
-
Ongeveer 16%.
-
Ongeveer 68%.
-
-
50%
-
85%
-
`sigma_B = 50` en `mu_B = 1150` (uur).
-
Omdat de verdeling breder is en het gebied in beide gevallen 100% voorstelt, moet de hoogte minder zijn.
-
95%
-
2,5%
-
-
-
-
68%
-
2,5%
-
97,5%
-
2,5%
-
-
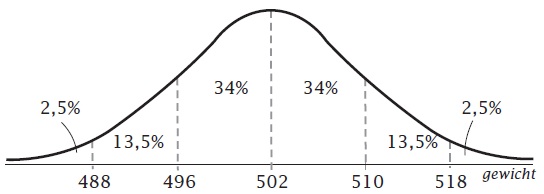
`mu = 3,0` en `sigma = 0,2`
`mu = 82` en `sigma = 6`.
-
Bovenste normaalkromme: gebied is 16%.
Onderste normaalkromme: gebied is 84%.
-
-
-
32%
-
84%
-
Nee, de vuistregels zijn hierbij niet te gebruiken.
-
Ongeveer 16% + 20% = 36%.
-
Ja, waarschijnlijk hebben ze gelijk.
-
-
68%
-
16%
-
84%
-
Onder een IQ van 85.
-
-
Tussen 32 en 64.
-
Tussen 32 en 80.
-
16%
-
-
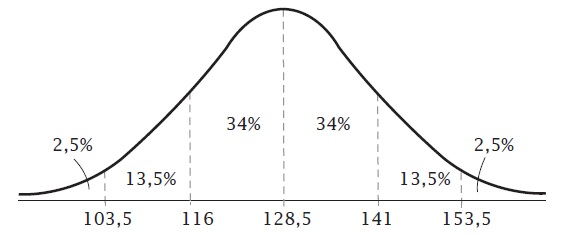
`mu = 162` cm en `sigma = 6,5` cm.
-
-
-
`a = 13`
-
168,5 cm.
-
-
-
84%
-
5%
-
Nee, de vuistregels zijn hierbij niet te gebruiken.



