Totaalbeeld

Samenvatten

Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Kansen en tellen. Een eigen samenvatting maken is nuttig.

Begrippenlijst:

11: kansexperiment — gebeurtenis — experimentele kans — relatieve frequentie — simulatie
12: aselect — theoretische kans — wet van de grote aantallen
13: wegendiagram — boomdiagram — venndiagram
14: n-faculteit — permutaties
15: permutaties — combinaties — driehoek van Pascal

Activiteitenlijst:

11: kansen bepalen op grond van kansexperimenten en/of simulaties
12: kansen bepalen op grond van redeneringen met even waarschijnlijke mogelijkheden
13: diagrammen gebruiken om mogelijkheden te tellen
14: machten en faculteiten gebruiken om mogelijkheden te tellen
15: mogelijkheden tellen met behulp van permutaties en combinaties en de driehoek van Pascal

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Kansen en tellen > Totaalbeeld > Achtergronden

Testen

  1. De Toto is een spel waarbij je voetbaluitslagen voorspelt. Bij Toto13 voorspel je van 13 wedstrijden of de thuisclub wint, verliest of gelijkspeelt.
    1. Hoe groot is de kans dat je een wedstrijd juist voorspelt als je geen enkel verstand van voetbal hebt? En als je wel verstand van voetbal hebt?
    2. Hoeveel verschillende Toto13 uitslagen zijn er in totaal mogelijk?
    3. Hoe groot is de kans dat je alle 13 wedstrijden goed voorspelt? (Gebruik flink wat decimalen...)
    4. Hoeveel Toto13 uitslagen zijn er met slechts 2 foute voorspellingen?
    5. Hoeveel Toto13 uitslagen zijn er met hoogstens 2 foute voorspellingen?
    6. Hoe groot is de kans dat je hoogstens twee wedstrijden fout voorspelt?

  2. Iemand werpt met twee viervlaksdobbelstenen. Dergelijke dobbelstenen hebben de vorm van een regelmatig viervlak met daarop de getallen 1, 2, 3 en 4. Er wordt gelet op de som van de getallen die onder komen te liggen.
    1. Simuleer met behulp van toevalsgetallen 40 worpen met twee van die dobbelstenen. Hoe groot is de experimentele kans op 4?
    2. Hoe groot is de theoretische kans op 4?

  3. Een gezin bestaat uit vier personen: vader Jan, moeder Jannie, kinderen Wim en Marietje. Twee van hen moeten de afwas doen. Wie dat zijn wordt bepaald door loting.
    1. Hoe groot is de kans dat beide kinderen de afwas moeten doen?
    2. Hoe groot is de kans dat beide mannelijke gezinsleden moeten afwassen?

  4. Het bekende dominospel bestaat uit 28 stenen. Elke steen bestaat uit twee helften. Op elke helft komen 0, 1, 2, 3, 4, 5, of 6 ogen voor. Je kiest aselect één steen.
    1. Laat zien waarom er 28 dominostenen zijn.
    2. Hoe groot is de kans dat het een "dubbele" is (aan beide kanten evenveel ogen)?
    3. Hoe groot is de kans dat de som van het aantal ogen minstens 10 is?
    4. Hoe groot is de kans dat het verschil van het aantal ogen hoogstens 2 is?
    5. Hoe groot is de kans dat het grootste aantal ogen op één van beide zijden 3 is?
    6. Je speelt met Petra een spelletje domino. De hiernaast getekende stenen heb jij bij het delen gekregen. Jij begint het spel met de "dubbel-vijf". Hoe groot is de kans dat zij kan aanleggen?

  5. Er worden voor Sinterklaas in een gezin van vier personen lootjes getrokken. Als iemand zijn eigen naam trekt moet er opnieuw worden geloot.
    Hoe groot is de kans dat dit het geval is?

  6. Als je twee opeenvolgende verkiezingen voor de Tweede Kamer met elkaar vergelijkt, dan zie je dat mensen regelmatig van partij veranderen. Aan 415 Nederlanders die beide keren hebben gestemd is gevraagd op welke partij dat was. De gegevens staan in deze tabel. De categorie "overige" wordt opgevat als één partij.



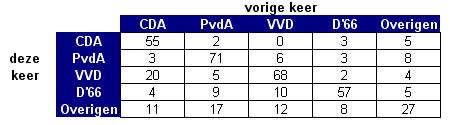
    Bereken in vier decimalen nauwkeurig de kans dat een willekeurig gekozen ondervraagde
    1. de vorige keer op het CDA stemde;
    2. deze keer op de PvdA stemde;
    3. weer op zijn eigen partij stemde;
    4. die de vorige keer op de PvdA stemde nu op het CDA stemde;
    5. die de vorige keer op D'66 stemde nu op een andere partij stemde.

  7. De leerlingenraad bestaat uit 22 personen, verdeeld over diverse jaargroepen. Er zitten 8 leerlingen uit de bovenbouw en 14 leerlingen uit de onderbouw in. Er moet een dagelijks bestuur worden gekozen van vijf personen (voorzitter, secretaris, penningmeester, vice-voorzitter en vice-secretaris).
    1. Op hoeveel manieren kun je dit dagelijks bestuur kiezen als ze pas achteraf de functies onderling verdelen?
    2. Op hoeveel manieren kun je dit dagelijks bestuur samenstellen als de leden in functie worden gekozen?
    3. Op hoeveel manieren kun je het dagelijks bestuur kiezen als het moet bestaan uit twee leerlingen uit de onderbouw en drie uit de bovenbouw?
    4. Op hoeveel manieren kun je het dagelijks bestuur kiezen als er minstens één onderbouwleerling deel van moet uitmaken?
    5. Op hoeveel manieren kun je het dagelijks bestuur kiezen als de voorzitter uit de bovenbouw moet komen?

Toepassen

  1. Mantoux-test

    Ongeveer 0,02% van alle mensen lijdt aan TBC (tuberculose). Om te onderzoeken of iemand met TBC is besmet wordt er vlak onder de huid een stof ingebracht waarop 98% van de mensen die aan tbc lijden positief reageert. Echter ook ongeveer 1% van de mensen die niet aan TBC lijden reageert er positief op. Deze test heet de Mantoux-test.
    1. Maak van de gegevens een tabel. Ga uit van 1.000.000 mensen.
    2. Iemand ondergaat deze Mantoux-test en reageert positief. Hoe groot is de kans dat hij niet aan tbc lijdt?

  2. Erfelijkheid

    Een bekende toepassing van de kansrekening in de biologie is de erfelijkheidsleer. Lees hierover:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Kansen en tellen > Totaalbeeld > Toepassingen

    Cavia's komen voor in drie kleuren, bruingeel, lichtgeel en wit. Die kleurenworden bepaald door een gen dat in twee typen voorkomt, te weten B en b. Een cavia van het type BB is bruingeel, een cavia van het type bb is wit, een cavia van het type Bb is lichtgeel.
    1. Een bruingele cavia wordt gekruist met een witte cavia. Stel de bijbehorende kruisingsmatrix op.
    2. Lichtgele cavia's worden onderling gekruist. Dit levert 134 bruingele, 265 lichtgele en 137 witte cavias op. Verklaar deze aantallen met behulp van een kruisingsmatrix.
    3. Wat kun je verwachten van de nakomelingen bij de kruising van een lichtgele en een witte cavia?

Examenopgaven

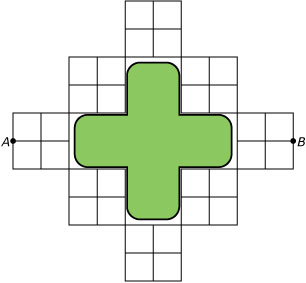  1. Hier zie je een plattegrond van paden rond een kruisvormige vijver. Een route van `A` naar `B` moet zo kort mogelijk zijn en mag niet buiten de paden leiden. Hoeveel routes van `A` naar `B` zijn er mogelijk?

    (bron: examen wiskunde A havo 1989, eerste tijdvak)