
Permutaties en combinaties
Antwoorden bij de opgaven
-
-
In de voorrondes hoef je alleen bij de eerste drie te zijn om door te gaan.
Of je eerste, tweede of derde bent maakt dan geen verschil, in de finale natuurlijk wel.
-
Omdat de 3! volgordes binnen de eerste drie dan als 1 volgorde tellen.
-
`56`
-
Zie practicum.
-
`161700`
-
-
-
-
`15`
-
-
`((20),(5))=15504`
-
`(20!)/(15!)=1860480`
-
-
-
-
`((8),(3))*((12),(2))=3696`
-
`((8),(3))*((12),(2))+((8),(2))*((12),(3))+((8),(1))*((12),(4))+((8),(0))*((12),(5))=14608`
-
-
Zie figuur.
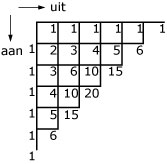
-
Zie figuur.
-
`1`
-
`7`
-
`21`
-
Als er `3` aan zijn, dan zijn er `4` uit.
Het aantal manieren daarvoor is gelijk aan het aantal manieren om er `4` aan te zetten, zodat er 3 uit zijn.
Het roosterdiagram is symmetrisch.
-
-
`30`
-
`30 * 29 * 28 * 27 = 657720` manieren.
-
`4! = 24`
-
`657720/24 = 27405`
-
Op `(30!)/(24!*6!) = 593775` manieren.
-
-
`35`
-
`10`
-
`35*10=350`
-
-
Bij de zesde stap ga je omhoog, dus het antwoord is "nee".
-
Hier is sprake van een greep van 3 uit 7, dus er zijn `(10!)/(3!*7!) = 120` lijsten mogelijk.
-
`2^10 = 1024`
-
`1/1024`
-
-
De uitkomst is 0, 1, 2, 3, 4 of 5 keer kruis. Er zijn dus 6 mogelijkheden.
-
`(5!)/(2!*3!) = 10`
-
`10/(2^5) = 10/32`
-
Er zijn in totaal `2^50` mogelijkheden.
Het aantal gunstige mogelijkheden is `(50!)/(20!*30!)`.
De kans is daarom ongeveer 0,0419.
-
Elke wedstrijd is een greep van twee spelers uit de 24 waarbij de volgorde niet van belang is.
Er zijn dus `((24),(2)) = (24!)/(2!*22!) = 276` wedstrijden te spelen.
-
-
`((14),(4))=1001`
-
`((14),(2)) * ((12),(2))=6006`
-
-
Rooster I: `((7),(5)) * ((6),(3)) = 420` routes.
-
Rooster II: `((7),(5)) * 1 * ((4),(3)) = 84` routes.
-
-
`8! = 40320`
-
`6! * 3! = 4320`
-
`6! * 2 = 1440`
-
`((8),(3)) * 5! = 6720`
-
-
`6*6*6=216`
-
P(4,4,4) = `1/216`; P(3,3,6) = `3/216`; P(3,4,5) = `6/216`; P(2,4,6) = `6/216`; P(2,5,5) = `3/216`
-
-
`((12),(6))=924`
-
`6! = 720`
-
-
`26! = 4,0329... * 10^26`
-
`26 * 25 * 24 * 23 * 22 = 7893600`
-
`((26),(5))=65780`
-
Twee meisjes kies je op `((10),(2))=45` manieren.
Drie jongens kies je op `((16),(3))=560` manieren.
Totaal `45 * 560 = 25200` manieren.

