Totaalbeeld

Samenvatten

Je hebt nu alle theorie van "Rijen" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:
21: rij, termen van een rij — directe formule — recursie en recursieformule
22: verschilrij — somrij
23: rekenkundige rij — somformule van een rekenkundige rij
24: meetkundige rij — somformule van een meetkundige rij
25: discreet dynamisch model

Activiteitenlijst:
21: rijen beschrijven met een directe formule — rijen beschrijven met een recursieformule
22: de verschilrij van een rij bepalen — de som van (de eerste) n termen van een rij berekenen
23: werken met rekenkundige rijen, o.a. de somformule toepassen
24: werken met meetkundige rijen, o.a. de somformule toepassen
25: meetkundige rijen toepassen bij discrete dynamische modellen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Totaalbeeld > Achtergronden

Testen

1. Stel bij deze rijen zowel een mogelijke directe formule als een mogelijke recursieformule op.
   1. `7, 14, 28, 56, 112, ...`
   2. `5, 8, 11, 14, 17, ...`


2. Bekijk de rijen uit de vorige opgave nog eens.
   1. Welke van beide rijen zou een rekenkundige rij kunnen zijn? Licht je antwoord toe.
   2. Bereken van de rekenkundige rij bedoeld in a de som van de eerste 100 termen.
   3. Bekijk nu de andere rij. Waarom zou dat een meetkundige rij kunnen zijn? Motiveer weer je antwoord.
   4. Bereken van de meetkundige rij bedoeld in c de som van de eerste 100 termen.


3. Kees betaalt elk jaar op 1 januari premie voor een inboedelverzekering. De maatschappij waarbij hij verzekerd is belegt dat geld. Gemiddeld maken ze daarmee per jaar 9% winst.
   Na 16 jaar te hebben betaald krijgt Kees op 2 januari een schadegeval van € 3500, dat door de polis wordt gedekt. De verzekeringsmaatschappij betaalt hem dus uit.
   Heeft de maatschappij nu winst of verlies geleden op de verzekering van Kees?
   Geef een duidelijke toelichting.
   


4. Een gepensioneerde heeft een kapitaal `K` op de bank dat uitstaat tegen 7,2% rente per jaar. De bank schrijft elke laatste dag van de maand rente over het dan aanwezige saldo bij. Op elke eerste dag van de maand neemt deze gepensioneerde een bedrag `O` op, de eerste opname vindt één maand na storting van het beginkapitaal plaats.
   1. Toon aan dat het saldo na de `n`de opname is:
      `S_n = (1,0058)^n * K - (1,0058^(n-1) + 1,0058^(n-2) + · · · + 1,0058 + 1) * O`
   Neem nu aan dat `K = 100000` en `O = 2000`, beide in euro.
   2. Hoe groot is het saldo na 12 opnamen?
   3. Na hoeveel maanden is het kapitaal op deze manier "op"? Leg ook uit waarom er aanhalingstekens zijn gebruikt.


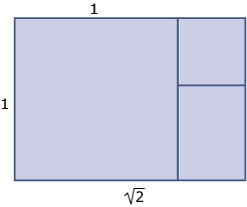5. Een A4'tje is een vel papier van (afgerond) 297 mm bij 210 mm.
   1. Ga na dat de lengte en de breedte zich verhouden als `sqrt(2) : 1` (bij goede benadering).
   Twee A4'tjes met de lange zijden tegen elkaar vormen een vel A3.
   2. Ga na dat de lengte en de breedte van een A3 zich ook verhouden als `sqrt(2) : 1` (bij goede benadering).
   3. Ga na: als je een rechthoek met breedte b en lengte b2 in twee gelijke helften verdeelt door een lijn evenwijdig met de korte zijden, verhouden de lengte en de breedte van de twee helften zich weer als `sqrt(2) : 1`.
   Het standaardvel A0 is (afgerond) 1189 mm bij 841 mm. Halveren geeft A1; nog drie keer halveren geeft A4.
   4. Ga na dat de oppervlakte van zo'n vel A0 praktisch 1 m² is.
   5. Laat `l_n` de lengte in m zijn van A`n`. Stel een recursieformule en een directe formule op voor de rij `l_0, l_1, l_2, ...`
   6. Doe hetzelfde voor de rij der oppervlakten van A`n` (kies zelf namen en eenheden).
   7. Bereken nauwkeurig de lengte en breedte van een vel A0 uit de gegevens: de oppervlakte is 1 m² en lengte en breedte verhouden zich als `sqrt(2) : 1`.


6. Een gasfles is gevuld met een hoeveelheid gas onder druk. De fles loopt langzaam leeg door een lekkende afsluiter. Het verlies per uur is recht evenredig met de druk in de fles, dus ook met de hoeveelheid gas in de fles.
   Stel per uur is het verlies een fractie 4% van de aan het begin van het uur aanwezige gas. Aan het begin is de hoeveelheid gas 100 liter, na 1 uur is dus `0,04 * 100` liter ontsnapt, in het 2-de uur ontsnapt `0,04 * (100 - 0,04 * 100)` liter.
   1. De hoeveelheden nog aanwezig gas na 0, 1, 2, ... uur vormen een meetkundige rij. Met welke reden? Stel een directe formule voor die rij op.
   2. Hoeveel ontsnapt dus in het `n`-de uur?
   3. Zowel uit het antwoord bij a als uit dat bij b kun je een formule halen voor de hoeveelheid gas die in de eerste `n` uur ontsnapt. Ga na of je hetzelfde krijgt.


7. Bij de geboorte van zijn eerste kleinzoon stopt opa € 50,- in een potje. Bij de eerste verjaardag doet hij daar € 100,- bij, bij de tweede verjaardag € 150,-, enzovoort, telkens € 50,- meer. Hij doet dat voor het laatst op de zestiende verjaardag, en geeft dan meteen het hele bedrag aan zijn kleinzoon.
   1. Hoe groot is dat bedrag?
   Bij de geboorte van haar eerste kleindochter pakt oma het anders aan. Zij stort € 350,- op een spaarrekening die 3% rente per jaar geeft, en herhaalt dit jaarlijks, voor het laatst op de zestiende verjaardag.
   2. Hoe groot is het bedrag op de spaarrekening op de dag na de zestiende verjaardag? (Je hoeft er geen rekening mee te houden dat de bank de rente op centen afrondt).
   Bij de geboorte van die kleindochter pakt de andere oma het nog anders aan. Zij werkt met dezelfde bedragen als de opa, maar stort ze op een spaarrekening die 3% rente per jaar geeft.
   3. Hoe groot is het bedrag op de spaarrekening op de zestiende verjaardag?


8. Pas gezette koffie heeft een temperatuur van zo’n 80°C. Schenk je deze koffie in een kopje en zet je dat in de kamer dan wordt de temperatuur lager totdat hij de kamertemperatuur (20°C) benadert.
   De daling van de temperatuur per minuut is recht evenredig met het temperatuursverschil met de omgeving.
   1. Leg uit, dat hieruit deze differentievergelijking is af te leiden: `T_(t+1) = T_t + c * (T_t - 20)`, waarin `t` het aantal minuten voorstelt na het inschenken.
   Neem aan dat `c = -0,05`.
   2. Maak een grafiek van de rij `T_t`. Welke grenswaarde zal de rij `T_t` bereiken?
   3. Laat zien hoe de grenswaarde uit de gegeven recursieformule is af te leiden.
   4. Bepaal na hoeveel minuten de temperatuur van de koffie minder dan 1°C verschilt van de kamertemperatuur.

Toepassen

9. Hypotheekvormen

   De geldlening bij een bank die meestal nodig is voor het kopen van een huis noem je een hypotheek. Je bouwt dan bij de bank een hypotheekschuld op die je op meerdere manieren kunt aflossen. Lees daartoe

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Totaalbeeld > Toepassingen
   

   Stel je voor dat je op 1 januari van een bepaald jaar een hypotheek van € 240.000,00 afsluit tegen een rente van 4% per jaar met een looptijd van 30 jaar. Je betaalt rente en aflossing telkens aan het einde van een jaar.
   1. Bij een "lineaire hypotheek" betaal je elk jaar evenveel aflossing en rente over de restschuld. Maak hierbij een tabel van jaarlijks te betalen bedragen en bereken het totaalbedrag dat je hiervoor kwijt bent als de situtatie zich verder niet wijzigt.
   2. Bij een "annuïteitenhypotheek" betaal je elk jaar een vast bedrag. Bereken de grootte van dit bedrag en het totaalbedrag dat je hiervoor kwijt bent als de situtatie zich verder niet wijzigt.
   3. Zoek eens uit welke hypotheekvormen er verder nog bestaan. Reken bij minstens één daarvan de kosten na.



10. Varkenscyclus

    In de economie is de varkenscyclus een bekend dynamisch vraag-en-aanbodmodel. Op de varkensmarkt kunnen de aanbieders van varkens namelijk niet onmiddellijk reageren op een prijsverandering omdat het vetmesten van varkens tijd kost. Lees hierover in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Totaalbeeld > Toepassingen
    

    Bekijk ook het bijgevoegde Excel-bestand.
    1. Leg uit dat de gegeven modelformules in overeenstemming zijn met de aannamen.
    2. Waar vind je de periode van 0,5 jaar (nodig voor het vetmesten van een varken) terug?
    3. Welke evenwichtspriijs levert het model op?
    4. Stel een differentievergelijking op voor de rij `p(t)` er van uitgaande dat vraag en aanbod elkaar in evenwicht houden.



11. Prooidier-roofdier modellen

    Bekijk eerst de pagina over prooi-roofdier modellen op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Totaalbeeld > Toepassingen
    

    Het is nu de bedoeling dat je hier zelf mee aan de slag gaat. Zoek eventueel meer informatie en maak gebruik van Excel.
    Dit is een mooi onderwerp voor een praktische opdracht of zelfs een profielwerkstuk.
    

Examenopgaven

12. Ureum-gehalte

    De kwaliteit van het water in zwembaden wordt onder andere beoordeeld op grond van het ureumgehalte. Ureum komt in het water via zweet en urine. Metingen hebben aangetoond dat bij 1000 bezoekers per dag de hoeveelheid ureum in het water op die dag met 500 g toeneemt. Om te voorkomen dat er te veel ureum in het water komt, moet er zo ververst worden dat de wettelijke norm van 2 g ureum per m³ water niet overschreden wordt. In een model gaan we er van uit dat dagelijks 1000 bezoekers een bad van 1000 m³ bezoeken en dat de verversing van het water ’s nachts plaatsvindt. Voor verversing rekent men 30 liter per persoon per dag. Dat betekent in dit model dat ’s nachts 30 m³ ververst wordt (dus 3% van het totaal). We beginnen de eerste dag met 0 g ureum in het water. Aan het eind van de dag zit er 500 g ureum in het water. Na het verversen is er dan aan het begin van de tweede dag 485 g ureum over.
    1. Laat door berekening zien dat er aan het begin van de derde dag ruim 955 g ureum in het water zit.
    2. In de loop van welke dag wordt de wettelijke norm overschreden? Licht je antwoord toe.
    Het blijkt dat 30 liter per bezoeker per dag verversen niet voldoende is. In plaats van 30 liter wordt daarom 200 liter genomen.
    3. Toon aan dat voor de hoeveelheid ureum (notatie `U_n`) aan het begin van de `n`de dag dag geldt `U_n = 0,8 * U_(n-1) + 400`.
    Stel je voor dat het water 0 g ureum aan het begin van de eerste dag bevat.
    4. Toon aan dat de hoeveelheid ureum in gram aan het begin van de `n`de dag rechtstreeks kan worden berekend met de formule: `U_n = 2000 - 2500 * (0,8)^n`.
    5. Leg met behulp van deze formule uit dat aan het begin van elke dag aan de wettelijke norm wordt voldaan.
    6. In de loop van de dag kan de wettelijke norm wél worden overschreden. Bereken op welke dag dat voor het eerst gebeurt.

    (bron: examen wiskunde A havo van voor 1990)




13. Nationaal inkomen

    In de afgelopen 20 jaar is het wereldinkomen (het totale inkomen van alle mensen samen) sneller gegroeid dan de wereldbevolking. Dat betekent dat het gemiddeld inkomen per hoofd van de bevolking is gestegen. In de theorie van de economische groei spelen de kapitaalgoederen een belangrijke rol. Bij kapitaalgoederen kun je bijvoorbeeld denken aan machines. De kapitaalgoederen hebben een grote invloed op de productie. Hier zie je een eenvoudig model voor economische groei:
    • `I_t = S_t`.
      `I_t` zijn investeringen in jaar `t`; `S_t` zijn besparingen in jaar `t`. De investeringen zijn steeds gelijk aan de besparingen.
    • `I_t = K_(t+1) - K_t`.
      `K_t` is hoeveelheid kapitaalgoederen in jaar `t`. De investeringen leiden uitsluitend tot uitbreiding van de kapitaalgoederen.
    • `S_t = s * Y_t`.
      `Y_t` is het nationaal inkomen in jaar `t`. De besparingen zijn steeds een vast gedeelte van het nationaal inkomen; `s` heet de spaarquote.
    • `K_t = k * Y_t`.
      De hoeveelheid kapitaalgoederen is gelijk aan `k` keer de productiecapaciteit. Omdat wordt aangenomen dat de productiecapaciteit volledig worden benut, is de productiecapaciteit gelijk aan het nationaal inkomen; `k` heet de kapitaalcoëfficiënt.
    Kies `s = 0,3`, `k = 2` en `K_0 = 200`. Alle bedragen zijn steeds in miljoenen dollars.
    1. Toon aan dat volgens het model geldt: `K_(t+1) = 1,15 * K_t`.
    2. Voor welke `t` geldt dat het nationaal inkomen `Y_t` voor het eerst boven de 1 miljard dollar komt? Licht je antwoord toe.
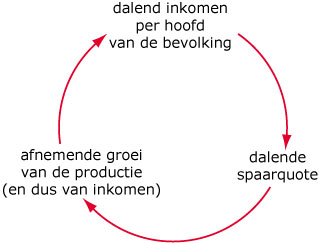
    De spaarquote en de kapitaalcoëfficiënt bepalen de groei van het nationaal inkomen. Ontwikkelingslanden hebben lage gemiddelde inkomens en kunnen nauwelijks sparen: `s` is laag. In de figuur zie je dat dit leidt tot een vicieuze cirkel van armoede.
    3. Toon aan dat ook volgens het model geldt: als `s` afneemt, dan neemt de groei van het nationaal inkomen af.

    (bron: voorbeeldexamen vwo wiskunde A1,2 uit 1998)