Discrete dynamische modellen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Discrete dynamische modellen > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Discrete dynamische modellen > Uitleg

Opgaven

1. In de Uitleg zie je een voorbeeld van een discreet dynamisch model.
   1. Waarom heet dit model zo?
   2. Vanuit de recursieformule wordt een directe formule afgeleid. Schrijf die formule korter met behulp van de somformule voor een meetkundige rij.


2. Een bosbouwer verkoopt hout van bomen die hij zelf aanplant. Stel je voor dat hij op een bepaald stuk bos ongeveer 5000 bomen heeft geplant. Na een aantal jaren zijn de eerste bomen groot genoeg om te kunnen worden gekapt. Maar om ook daarna elk jaar opbrengst van dit perceel te hebben zal hij
   • de meeste bomen moeten laten staan;
   • nieuwe bomen aanplanten.
   Hij besluit elk jaar 15% van de bomen te kappen en dan weer 1000 aan te planten. Hij plant dus meer aan dan hij kapt, teneinde de opbrengst te verhogen. Op dit perceel is namelijk wel ruimte voor zo’n 6000 bomen.
   1. Onderzoek hoe het aantal bomen dat er jaarlijks op dit perceel staat, gaat verlopen. Maak een grafiek.
   2. Zal het aantal bomen de 6000 gaan overstijgen, denk je?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Discrete dynamische modellen > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. Bekijk in de Theorie wat een lineaire differentievergelijking is.
   Stel je voor dat je bij een bank een rentepercentage van 12% per jaar kunt krijgen. Je spaart € 1500,00 per jaar en je bent gestart op 1 januari 2000.
   1. Stel een lineaire differentievergelijking op voor `K(t)`, het kapitaal aan het begin van het `t`-de jaar.
   2. Maak een tijdgrafiek bij de rij met saldi. Wat gebeurt er met het saldo als `t` toeneemt?
   3. Op welk tijdstip is het saldo meer dan € 20000,00?


4. In Voorbeeld 1 tref je een model aan voor het kappen en aanplanten van bos.
   1. Leg uit hoe de lineaire differentievergelijking in dit voorbeeld uit de gegevens kan worden afgeleid.
   2. Maak zelf een tabel van het aantal bomen met je grafische rekenmachine en bepaal de grenswaarde voor het aantal bomen.
   3. Laat zien hoe je met behulp van de somformule voor een meetkundige rij de directe formule voor `B(t)` af kunt leiden.
   4. Leg uit hoe je de grenswaarde van 5556 bomen uit de directe formule kunt afleiden.


5. In Voorbeeld 2 wordt het logistische groeimodel beschreven.
   De groei van een aantal bacteriën wordt bij benadering beschreven door de differentievergelijking:

   `N(t) = k * N(t-1) * (400 - N(t-1))`

   waarin `N` het aantal bacteriën op tijdstip `t` (in dagen) is. Op `t = 0` zijn er 50 stuks. Neem eerst `k = 0,005`.
   1. Laat met behulp van een grafiek zien dat het aantal bacteriën niet onbeperkt toeneemt.
   2. Bepaal de grenswaarde waar `N` naar toe groeit.
   3. Is er voor elke waarde van `N(0)` sprake van een stabiele grenswaarde?
   4. Neem vervolgens `k = 0,01`. Is er nu sprake van een grenswaarde voor `N(t)` als `N(0) = 50`?


6. In Voorbeeld 3 zie je een stelsel van twee lineaire differentievergelijkingen.
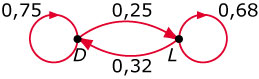
   Stel je voor dat er maar twee softwarebedrijven zijn die een internetbrowser op de markt brengen. Noem die browsers bijvoorbeeld "Discoverer" en "Landscape". Beide bedrijven beconcurreren elkaar heftig, zodat de gebruikers van een internetbrowser jaarlijks reikhalzend uitzien naar de nieuwste versie van de Discoverer of van Landscape. Ervaren gebruikers wisselen ook nogal eens van browser. In deze graaf zie je de wisselingen in beeld gebracht.
   1. Stel bij deze graaf een stelsel differentievergelijkingen op. Noem het aantal gebruikers van de Discoverer `D(t)` en dat van Landscape `L(t)`.
   2. Maak op je grafische rekenmachine de grafieken van de rijen `D(t)` en `L(t)` voor `n = 0, 1, ... , 10`. Ga er van uit dat `D(0) = 0,5` en `L(0) = 0,5`.
   3. Bereken met die differentievergelijkingen hoeveel procent van de gebruikers uiteindelijk in de evenwichtssituatie de Discoverer zal gebruiken.

Verwerken

7. Je hebt onverwacht € 500.000 gekregen. Je zet dit bedrag op 1 januari 2000 op een renterekening tegen 5% rente per jaar. Je haalt elke maand € 2500, van de bank om je inkomen mee aan te vullen. Het saldo van de renterekening `S_n` verandert daardoor maandelijks.
   1. Stel hierbij een recursieformule op.
   2. Maak een grafiek van de rij `S_n`. Beschrijf het verloop van het saldo.
   3. Na hoeveel jaar is het geld op deze renterekening op?
   4. Stel een directe formule op voor het saldo `S_n`.


8. In 2000 leefden er in een natuurgebied 2000 konijnen. Hun aantal is in de jaren daarna telkens met 5% toegenomen.
   1. Stel een recursieformule op voor het aantal konijnen `K(t)` waarin `t` het aantal jaren na 2000 is.
   2. Stel een directe formule op voor `K(t)`.
   3. Maak een grafiek en een tabel van de rij `K(t)`. In welk jaar is het aantal konijnen meer dan verdubbeld?


9. Leonardo van Pisa (ongeveer 1180–1250) geeft in zijn boek "Liber Abaci" uit 1202 het volgende raadsel weer:
   "In een afgesloten gebied zet ik één paar konijnen. Dit paar werpt elke maand één paar jongen. Al die jongen krijgen op hun beurt ook weer jonge konijntjes, maar pas vanaf hun tweede levensmaand en dan ook weer elke maand één paar jongen. Hoeveel paren konijnen zijn er nu na één jaar?"
   1. Stel een recursieformule op voor het aantal konijnen `A` na `n` maanden.
   2. Onderzoek hoe de toename van deze konijnen gaat verlopen met behulp van je grafische rekenmachine.
   3. Beantwoord de vraag die Leonardo van Pisa in zijn raadsel stelt.


10. Als je melk uit de koelkast haalt en in een glas schenkt loopt de temperatuur op vanaf `T(0) = 6`°C (de temperatuur binnen de koelkast) naar de kamertemperatuur van 20°C. De toename van de temperatuur per minuut is recht evenredig met het temperatuursverschil met de omgeving.
    1. Leg uit, dat hieruit deze recursieformule is af te leiden: `T(t+1) = T(t) + c * (20 - T(t))` waarin `t` het aantal minuten voorstelt.
    Neem aan dat `c = 0,1`.
    2. Maak een grafiek van deze rij en bepaal na hoeveel minuten de temperatuur van de melk minder dan 1°C verschilt van de kamertemperatuur.
    3. Laat zien hoe de grenswaarde uit de gegeven recursieformule is af te leiden.


11. Er wordt een nieuw maandblad voor jongeren opgericht. Aanvankelijk groeit het aantal abonnees sterk. Van het eerste blad werden 3000 exemplaren verkocht, maar van het tweede waren dat er al 5670, een stijging van ongeveer 90%. De redactie hoopt dat het aantal abonnees voorlopig met hetzelfde percentage zal blijven stijgen.
    1. Stel een daarbij passende differentievergelijking voor het aantal abonnees `A(t)` in maand `t`. Neem aan dat `t = 0` de maand van de eerste oplage voorstelt.
    2. Waarom is dit groeimodel voor het aantal abonnees van dit blad onwaarschijnlijk?
    Na verloop van tijd wordt de groei van het aantal abonnees echter kleiner. Voor `A(t)` blijkt de volgende recursieformule te gelden:

    `A(t) = 1,95 * A(t - 1) - 0,00002 * (A(t - 1))^2`

    3. Teken de bijpassende grafiek, weer uitgaande van `A(0) = 3000`.
    4. Op hoeveel abonnees zal dit maandblad uiteindelijk uitkomen?


12. Economen beschrijven de economie van een land wel met behulp van een discreet dynamisch model met meerdere vergelijkingen. Een eenvoudig model (waarin de overheid geen rol speelt) wordt beschreven door de vergelijkingen:
    • `I_t = 30`: de particuliere investeringen bedragen elk jaar 29 miljard euro;
    • `Y_t = C_t + I_t`: het nationaal inkomen `Y_t` is de som van de particuliere investeringen en de particuliere consumptie;
    • `C_t = 0,8 * Y_(t-1) + 10`: de particuliere consumptie in een bepaald jaar is 10 miljard meer dan 80% van het nationaal inkomen van het voorgaande jaar.
    Weet je nu het nationaal inkomen `Y_0` bij de start van dit model, dan kun je onderzoeken hoe dit nationaal inkomen zich in de loop van de jaren zal ontwikkelen.
    1. Stel een bijpassende differentievergelijking op voor het nationaal inkomen.
    2. Teken een grafiek van `Y_t` met `Y_0 = 190` miljard.
    3. Stel een directe formule op voor `Y_t`.
    4. Bereken het evenwichtsniveau van het nationaal inkomen.
    5. Hoe verandert het evenwichtsniveau van het nationaal inkomen als de particuliere investeringen met 10 miljard worden vergroot?

Testen

13. Iemand heeft een miljoen op de bank gezet tegen een rente van 6% per jaar. Hij gaat er van leven en haalt maandelijks € 1500,- van deze rekening voor zijn levensonderhoud.
    1. Stel hierbij een lineaire differentievergelijking op.
    2. Teken een bijpassende grafiek en bepaal daarmee of de rij van saldi `S_t` naar een grenswaarde toegroeit.
    3. Stel een directe formule op voor `S_t` en leid ook daaruit de evenwichtswaarde af.


14. Een viskwekerij heeft een bepaald bassin waarin maximaal 5000 meervallen kunnen leven. De kweker zet daarin 1000 meervallen uit. Het aantal meervallen zal dan gaan groeien, maar omdat er maximaal 5000 meervallen in het bassin kunnen leven, zal de groei gaan afnemen naarmate het aantal meervallen dichter bij de 5000 komt.
    De kweker veronderstelt daarom dat de toename van het aantal meervallen per jaar recht evenredig is met het verschil tussen het aantal meervallen en het maximale aantal van 5000: `Delta
    N_t = c * (5000 - N_t)`, waarin `N_t` het aantal meervallen na `t` jaar is.
    1. Is er hier sprake van een logistisch groeimodel?
    2. Toon aan dat de veronderstelling van de kweker leidt tot een groeimodel met als bijbehorende differentievergelijking: `N_(t+1) = (1 - c) * N_t + 5000 * c`.
    3. Na een jaar zijn er ongeveer 1600 meervallen in het bassin. Bereken `c`.
    4. Teken een grafiek van `N_t`. Vanaf welk moment gaat het aantal meervallen minder snel toenemen?