Verschilrijen en somrijen

Inleiding

Heb je te maken met een vaste huurverhoging per jaar, dan weet je hoeveel je jaarlijks meer moet gaan betalen voor je studentenkamer. Maar heb je een vaste procentuele huurverhoging, dan weet je dat niet onmiddellijk. Je betaalt dan immers een vast percentage van steeds hoger wordend bedrag.
En hoe zit het met het bedrag dat je in totaal kwijt bent als je bijvoorbeeld de kamer vijf jaar huurt?

Je leert nu:

• het begrip verschilrij en het begrip somrij;
• notaties voor verschilrijen en somrijen;
• de som van een aantal termen van een rij berekenen met de rekenmachine.

Je kunt al:

• rijen in beeld brengen met bijvoorbeeld de grafische rekenmachine;
• werken met directe formules en recursieformules.

Verkennen

Stel je huurt een kamer voor 240 euro per maand, dus € 2880,00 per jaar.

1. bij een jaarlijkse huurverhoging van 60 euro betaal je
   h₁(n) = 2880 + n · 60 euro/jaar.
2. bij een jaarlijkse huurverhoging van 2% betaal je
   h₂(n) = 2880 · 1,02ⁿ euro/jaar.

> Bij de eerste manier van huur verhogen betaal je elk jaar 60 euro meer. Hoe zit dat bij de tweede manier?
> En hoeveel ben je bij beide manieren telkens gerekend over de eerste vijf jaar in totaal kwijt?

Uitleg

Stel je huurt een kamer voor 240 euro per maand, dus € 2880,00 per jaar.

1. bij een jaarlijkse huurverhoging van 60 euro betaal je
   h₁(n) = 2880 + n · 60 euro/jaar.
2. bij een jaarlijkse huurverhoging van 2% betaal je
   h₂(n) = 2880 · 1,02ⁿ euro/jaar.

Bij de eerste manier van huur verhogen betaal je elk jaar 60 euro meer. Bij de tweede manier is dit telkens een ander bedrag. De rij V(n) = h₂(n) – h₂(n – 1) brengt die getallen in beeld. Dit is de verschilrij van rij h₂. Je geeft hem wel aan als V(n) = Δh₂(n).
Je kunt hem met de GR wel maken, maar dan alleen als je de directe formule van de rij in de functie-mode hebt ingevoerd. In de rij-mode kun je geen verschilrij maken.

Wil je weten hoeveel je over de eerste vijf jaar gerekend aan huur moet betalen, dan moet je S(4) = h₁(0) + h₁(1) + h₁(2) + h₁(3) + h₁(4) uitrekenen.
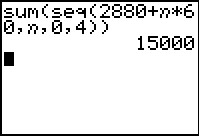Een korte schrijfwijze hiervoor is:
S(4) = ${\displaystyle \sum _{n=0}^4{h}_1(n)}$
Je rekenmachine heeft een aantal functies om dit mee te berekenen.
En voor rij h₂ gaat dit net zo...

‡

Opgaven

1. In de Uitleg is sprake van rijen van verschillen. Die verschilrijen maak je met je grafische rekenmachine. Maar dan moet je wel de directe formule van de rij hebben.
   1. Maak de verschilrij `V_1` bij `h_1`. Hij is nogal saai. Waarom is dat zo?
   2. Maak nu de verschilrij `V_2` bij `h_2`.
   3. Hoeveel is `V_2(5)`?
   4. Waarom bestaan `V_1(0)` en `V_2(0)` eigenlijk niet?


2. De verschilrijen in de Uitleg gaan over de jaarlijkse huurverhoging. Maar je kunt ook kijken naar het totaalbedrag dat je gerekend over een aantal jaren kwijt bent aan huur. Je moet daarvoor de termen van de rijen `h_1` en `h_2` optellen.
   1. `S_1(5) = h_1(0) + h_1(1) + h_1(2) + h_1(3) + h_1(4) + h_1(5)`. Hoe kun je dit korter opschrijven?
   2. Bereken `S_1(5)` met je grafische rekenmachine. Wat stelt dit bedrag precies voor?
   3. Bereken ook `S_2(5)` met je grafische rekenmachine.
   4. Is de procentuele huurverhoging de eerste zes jaar gunstiger?

Theorie

De verschilrij van een rij u(n) is de rij V(n) = Δu(n) = u(n) – u(n – 1).
Je kunt hem met de grafische rekenmachine maken, maar alleen als je een directe formule van de rij in de functie-mode hebt ingevoerd. In de rij-mode kun je geen verschilrij maken.

De somrij van een rij u(n) is de rij S(n) = u(0) + u(1) + u(2) + u(3) + ... + u(n).
Een korte schrijfwijze hiervoor is:
S(n) = ${\displaystyle \sum _{k=0}^{n}u(k)}$
Je rekenmachine heeft een aantal functies om dit mee te berekenen.
Pas er wel voor op dat de som van de eerste n termen gelijk is aan S(n – 1) omdat je bij 0 begint te nummeren.

Zo is de som van de derde tot en met de twintigste term gelijk aan:
S(19) – S(1) = ${\displaystyle \sum _{k=2}^{19}u(k)}$
Voor je rekenmachine is dat allemaal geen probleem...
Maar let wel goed op in situaties dat er genummerd wordt vanaf 1.

‡

Voorbeeld 1

Stel je huurt een kamer voor 240 euro per maand, dus € 2880,00 per jaar.
Bij een jaarlijkse huurverhoging van 2% betaal je h₂(n) = 2880 · 1,02ⁿ euro/jaar.
Stel een formule op voor jaarlijkse huurverhogingen.
Bereken de totale huurprijs over de eerste 10 jaren.

Antwoord

De formule voor de jaarlijkse huurverhogingen is de formule voor de verschilrij van h₂:
V(n) = Δh₂(n) = h₂(n) – h₂(n – 1) = 2880 · 1,02ⁿ – 2880 · 1,02^n – 1
Dit kun je herschrijven:
V(n) = 2880 · 1,02^n – 1 · (1,02 – 1) = 57,6 · 1,02^n – 1.
Merk op dat bij de verschilrij moet worden genummerd vanaf n = 1.

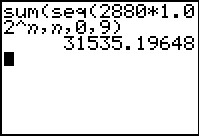
De totale huurprijs over de eerste 10 jaar is: S(9) = ${\displaystyle \sum _{n=0}^{9}2880\cdot {\mathrm{1,02}}^n}$.
Met de grafische rekenmachine vind je: S(9) ≈ 31535,20.

‡

Voorbeeld 2

Gegeven is de rij kwadraten door k_n = n² met n een geheel getal en n ≥ 1. Bekijk de verschilrij en stel er een formule voor op.
Stel op grond van de verschilrij een recursieformule voor de rij kwadraten op.

Antwoord

De verschilrij is V_n = Δk_n = n² – (n – 1)².
Haakjes uitwerken geeft: V_n = 2n – 1 met n ≥ 2.

Dus is k_n – k_n – 1 = 2n – 1.
En dat betekent: k_n = k_n – 1 + 2n – 1.
De recursieformule is daarom: k_n = k_n – 1 + 2n – 1 met k₁ = 1 en n geheel en n ≥ 2.

‡

Voorbeeld 3

De beroemde rij van Fibonacci is: 1,1,2,3,5,8,13,21,34,...
Wat valt je op als je de bijbehorende verschilrij bekijkt?
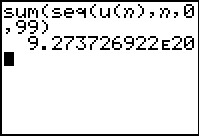
Bereken de som van de eerste 100 termen van deze rij.

Antwoord

De verschilrij is: 0,1,1,2,3,5,8,13,...
Behalve de eerste term is de verschilrij gelijk aan de rij zelf, alleen de nummering verschuift met 2. (Denk er om dat er geen nulde term is bij de verschilrij!)
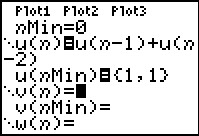
Noem nu de termen van de rij van Fibonacci f(n) met n = 0,1,2,3,4,...
Dan is dus de verschilrij: Δf(n) = f(n) – f(n – 1) = f(n – 2).
De rij van Fibonacci heeft daarom als recursieformule:
f(n) = f(n – 1) + f(n – 2) met f(0) = 1 en f (1) = 1.

Nu kun je de rij in de grafische rekenmachine invoeren en de som van de eerste 100 termen laten berekenen door de machine. (Het kost wat rekentijd...)

‡

Opgaven

3. In Voorbeeld 1 worden de verschil en som van een rij met huurprijzen nog eens bekeken.
   1. De nummering van de huurprijzen begint bij 0. Hoe zit dat met de verschilrij? En met de somrij?
   2. Maak een tabel van de verschilrij zonder er eerst een formule voor af te leiden.
   3. Voer zelf de afleiding van de formule voor de verschilrij uit. Ga na, dat de waarden van die verschilrij overeen komen met de tabel bij b.
   4. Leg uit, waarom de totale huurprijs over de eerste 10 jaren `S(9)` is en niet `S(10)`.
   5. Bereken met je grafische rekenmachine `sum_(n=0)^(8) 2880 * 1,02^n`. Wat heb je nu precies berekend?


4. In Voorbeeld 2 wordt de rij kwadraten bekeken.
   1. Leid zelf de formule voor de verschilrij `V_n` af. Waarom moet `n >= 2`?
   2. Bereken `V_100` zowel met behulp van de formule voor `V_n` als vanuit de kwadratenrij zelf.
   Bekijk nu de rij met derde machten: `d_n = n^3` voor `n >= 1`.
   3. Leid een formule af voor de verschilrij van `d_n`.
   4. Je ziet in Voorbeeld 2 hoe je door naar de verschilrij te kijken een recursieformule voor de kwadratenrij kunt maken. Maak nu een recursieformule voor de rij met derde machten.


5. In Voorbeeld 3 maak je kennis met de rij van Fibonacci. Je zult er later nog toepassingen van tegenkomen.
   1. Stel zelf de recursieformule van deze rij op.
   2. Bereken nu met je grafische rekenmachine de som van de eerste 20 termen van de rij van Fibonacci.


6. Gegeven is de rij `t(i) = 5i + 2` voor `i >= 0`.
   1. Stel een formule op voor de verschilrij `V(i)`.
   2. Bereken `sum_(i=0)^(5) t(i)`. Is dit nu de vierde, vijfde of de zesde term van de somrij `S(i)`? Is het `S(4)`, `S(5)` of `S(6)`?
   3. Welke termen van `t(i)` moet je optellen om `sum_(i=2)^(5) t(i)` te berekenen? Waarom is dit gelijk aan `S(5) - S(1)`?

Verwerken

7. Gegeven is de rij `t(n) = 2n + 1` met `n >= 0`.
   1. Schrijf de eerste zes termen van de verschilrij `V(n)` op.
   2. Schrijf de eerste zes termen van de somrij `S(n)` op.
   3. Bereken `S(19)`.
   4. Bereken `sum_(n=10)^(19) t(n)`.


8. Bekijk de rij 2, 3, 6, 11, 18, 27, 38, 51, ...
   Je hoeft niet op zoek te gaan naar een directe formule, hoewel die wel is te vinden. De `n`de term van deze rij is `u(n)` met `n >= 0`.
   1. Welke verschilrij hoort er bij deze rij?
   2. Beschrijf de verschilrij met een directe formule.
   3. Leid nu voor `u(n)` een recursieformule af.
   4. `S(n)` is de bijbehorende somrij. Bereken `S(20)`.
   5. Bereken ook `sum_(n=15)^(20) u(n)`.


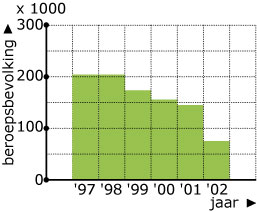9. Dit toenamediagram kun je opvatten als de weergave van zes termen van een verschilrij.
   1. Schrijf de grootte (ongeveer) van deze termen op.
   2. Stel dat de beroepsbevolking aan het begin van 1997 bestond uit 3 miljoen personen. Hoe groot ongeveer was dan de beroepsbevolking aan het eind van 1997? En aan het eind van 1999?
   3. Is er een verband tussen toenamediagrammen en verschilrijen?
   4. Welke uitspraken over de periode 1997 tot en met 2002 hieronder zijn juist?
      1. De beroepsbevolking is elk jaar toegenomen.
      2. Over de hele periode is de beroepsbevolking afgenomen.
      3. In 2002 is de beroepsbevolking minder toegenomen dan in 2001.
      4. Aan het eind van 2002 was de beroepsbevolking kleiner dan aan het eind van 2001.


10. De rij `t_0, t_1, t_2, ...` is gegeven door `t_n = 0,5n^2 + 1,5n + 1`.
    1. Schrijf de eerste tien termen van deze rij op.
    2. Schrijf de eerste negen termen op van de verschilrij.
    3. Schrijf de eerste acht termen op van de verschilrij van die verschilrij.
    Bekijk nu de rij `u_0, u_1, u_2, ...` met `u_n = n^2 + 5n`.
    4. Bepaal weer een stuk van de verschilrij en de verschilrij van de verschilrij. Is er een overeenkomst met het antwoord van c? Geef een verklaring.

Testen

11. De rij `u_0, u_1, u_2, ...` is gegeven door de directe formule `u_n = n^2 - n`.
    1. Bereken de eerste vijf termen van de verschilrij `V_n` van deze rij.
    2. Stel een directe formule op voor `V_n`. Maak hiermee een recursieformule voor `u_n`.
    3. Bereken de eerste vijf termen van de somrij van deze rij.
    4. Bereken `sum_(n=6)^(8) u_n`.