
Rijen beschrijven

Inleiding
Vaak heb je bij het voorspellen van groei- en vervalprocessen te maken met "losse" getallen. Denk maar aan het saldo van een spaarrekening met een maandelijkse rentebijschrijving, de wekelijkse tellingen van een bepaald soort vogels, etc.
Vooral het berekenen van het saldo op je spaarrekening is natuurlijk van groot belang...
Je leert nu:
- het begrip rij;
- rijen beschrijven met een directe formule;
- rijen beschrijven door middel van recursie.
Je kunt al:
- grafieken van functies tekenen en in beeld brengen met bijvoorbeeld de grafische rekenmachine;
- werken met functievoorschriften, functiewaarden berekenen.
Verkennen
Je hebt op 1 januari 2008 een saldo van € 1240,00.
En je besluit dat geld op een spaarrekening te zetten. Verder ga je aan het begin van elke maand 50 euro naar die spaarrekening overmaken, te beginnen op 1 februari 2008. Je krijgt aan het eind van elke maand rente van 0,5% over het saldo van dat moment. Je haalt voorlopig geen geld van deze spaarrekening en je doet ook geen andere stortingen.
> Hoe hoog is je saldo op 1 januari 2009?
> Wanneer is je saldo meer dan € 3000,00?
Uitleg
Stel je wilt een kamer huren voor 240 euro per maand, dus € 2880,00 per jaar.
Omdat je weet dat er jaarlijkse huurverhogingen zijn, wil je afspreken hoe hoog de jaarlijkse huurverhoging maximaal bedraagt. Je kunt dit op twee manieren afspreken:
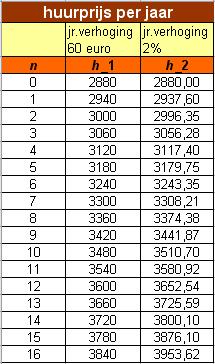
- De jaarlijkse huurverhoging is (maximaal) 60 euro.
- De jaarlijkse huurverhoging is (maximaal) 2%.
Om de huurprijzen te vergelijken zet je ze voor de komende jaren op een rij. Noem de huurprijs bij de eerste afspraak h1 en die bij de tweede h2. Je krijgt dan twee rijen getallen. De startdatum is 1 januari van een bepaald jaar en dan is het aantal huurjaren n = 0.
De rij getallen voor h1 kun je op twee manieren maken:
- De huurprijs na n jaren is: h1(n) = 2880 + n · 60.
Je berekent de huurprijs direct uit de huurjaren.
- De huurprijs na n jaren is 60 meer dan die na n – 1 huurjaren: h1(n) = h1(n – 1) + 60.
Je berekent de huurprijs door te kijken naar de prijs van het jaar ervoor. Dit heet recursie.
Voor de rij h2 gaat dit op vergelijkbare wijze.
‡
Opgaven
-
Bekijk het verhaal van het huren van een kamer in de Uitleg. Neem aan dat de jaarlijkse huurverhoging 60 euro is.
- Maak eerst zelf een tabel met huurprijzen voor `n = 0,1,2,3,4,...`
- Hoe heb je jouw tabel gemaakt: met behulp van recursie of door direct de prijzen te berekenen?
- Ligt zowel de formule bij de directe berekening als die bij de recursie toe. Leg duidelijk het verschil tussen beide uit.
-
Bij het verhaal in de Uitleg is ook sprake van een jaarlijkse huurverhoging van 2%.
- Maak ook hiervoor een tabel met huurprijzen voor `n = 0,1,2,3,4,...`
- Hoe heb je jouw tabel gemaakt: met behulp van recursie of door direct de prijzen te berekenen?
- Stel een formule op voor het berekenen van de huurprijs `h_2` door middel van recursie.
- Stel ook een formule op voor `h_2(n)` waarmee je de huurprijs van jaar `n` direct kunt berekenen.
Theorie
Een rij getallen u(n) is een functie waarbij n alleen de waarden 0,1,2,3,4,... (alle positieve gehele getallen en 0) aanneemt. De functiewaarden u(n) vormen de termen van de rij.
De eerste term van de rij is dan u(0), de tweede term is u(1), enz.
In plaats van u(n) wordt soms un geschreven.
In plaats van n wordt ook de letter t gebruikt, zeker als het om tijd gaat.
Meestal wordt de rij genummerd vanaf 0, maar als dat beter uitkomt wordt ook wel vanaf 1 genummerd. Voordeel van nummeren vanaf 0 is dat de formules vaak eenvoudiger zijn, nadeel is dat bijvoorbeeld de tiende term u(9) is.
Je kunt op twee manieren een formule voor een rij maken:
-
directe formule:
Elke term u(n) wordt direct berekend vanuit n, bijvoorbeeld: u(n) = 2880 · 1,02n.
Dit is vooral ook handig voor de grafische rekenmachine, want dan kun je een rij als functie invoeren. Zet je de stapgrootte in de tabel op 1, dan heb je de rij snel voor je neus. Maar directe formules zijn niet altijd gemakkelijk te vinden.
- recursieformule:
Elke term u(n) wordt berekend vanuit zijn voorganger u(n – 1), bijvoorbeeld:
u(n) = u(n – 1) · 1,02.
Maar dan moet wel de eerste term bekend zijn: u(0) = 2880.
Anders kun je de rij niet opbouwen vanaf het begin.
Je hebt op je grafische rekenmachine een speciale "mode" voor het rekenen met rijen.
Bekijk het practicum maar eens.
‡
Voorbeeld 1
Je wilt een kamer huren voor 240 euro per maand, dus € 2880,00 per jaar.
Bij een jaarlijkse huurverhoging van € 60 is de huurprijs na n jaren:
h1(n) = 2880 + n · 60.
Bij een jaarlijkse huurverhoging van 2% is de huurprijs na n jaren:
h2(n) = 2880 · 1,02n.
Bereken met je grafische rekenmachine tot welk jaar de huurverhoging in procenten voordeliger is.
Antwoord
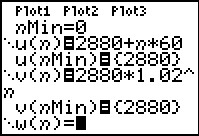
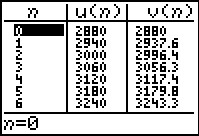
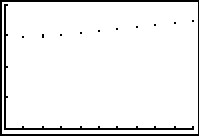
Omdat dit twee directe formules zijn kun je beide als functie in je GR invoeren.
Maar je rekenmachine heeft ook een speciale instelling om met rijen te werken. Daarmee maak je ook snel een tabel van beide rijen samen. Je ziet dat tot n = 6 de huurverhoging in procenten het gunstigst is.
‡
Voorbeeld 2
Je wilt een kamer huren voor 240 euro per maand, dus € 2880,00 per jaar.
Bij een jaarlijkse huurverhoging van € 60 is de huurprijs na n jaren:
h1(n) = h1(n – 1) + 60 met h1(0) = 2880.
Bij een jaarlijkse huurverhoging van 2% is de huurprijs na n jaren:
h2(n) = h2(n – 1) · 1,02 met h2(0) = 2880.
Bereken met je grafische rekenmachine tot welk jaar de huurverhoging in procenten voordeliger is.
Antwoord
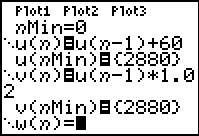
Omdat dit twee recursieformules zijn kun je beide alleen invoeren als je rekenmachine is ingesteld op werken met rijen. Dan maak je ook snel een tabel van beide rijen samen. Je ziet dat tot n = 6 de huurverhoging in procenten het gunstigst is.


‡

Voorbeeld 3
Je hebt op 1 januari 2008 een saldo van € 1240,00.
En je besluit dat geld op een spaarrekening te zetten. Verder ga je aan het begin van elke maand 50 euro naar die spaarrekening overmaken, te beginnen op 1 februari 2008. Je krijgt aan het eind van elke maand rente van 0,5% over het saldo van dat moment. Je haalt voorlopig geen geld van deze spaarrekening en je doet ook geen andere stortingen.
Wanneer is je saldo meer dan € 3000,00?
Antwoord
Nu is het maken van een directe formule nog niet eenvoudig. Maar de recursie is wel eenvoudig: je vermenigvuldigt telkens je saldo met 1,005 en telt er 50 euro bij op. Neem je t = 0 op 1-1-2008 en t in maanden, dan geldt voor het saldo S: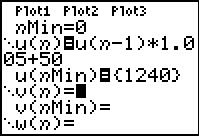
S(t) = S(t – 1) · 1,005 + 50 met S(0) = 1240.
Voer dit in je GR in en bekijk de tabel van de rij.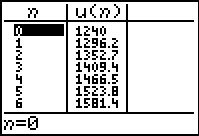 Op t = 30 zit je voor het eerst boven de 3000 euro. Dan heb je 30 maanden gespaard.
Op t = 30 zit je voor het eerst boven de 3000 euro. Dan heb je 30 maanden gespaard.
‡
Opgaven
-
Bekijk Voorbeeld 1.
- Waarom zijn de twee gegeven formules directe formules?
- Maak tabellen bij beide formules op je grafische rekenmachine in de functie-mode.
- Maak ook tabellen bij beide formules op je grafische rekenmachine in de rijen-mode. Doe eventueel eerst het Practicum.
- Ga na, dat tot `n = 6` de huurverhoging in procenten het gunstigst is.
-
Bekijk Voorbeeld 2.
- Waarom zijn de twee gegeven formules recursieformules?
- Maak tabellen bij beide formules op je grafische rekenmachine in de rijen-mode. Bekijk eventueel het Practicum nog eens.
- Maak grafieken bij beide rijen.
- Ga na, dat tot `n = 6` de huurverhoging in procenten het gunstigst is.
-
In Voorbeeld 3 wordt bekeken hoe je bij een rij een formule kunt maken. Een directe formule is altijd het handigst, dan hoef je de rij niet vanaf het begin op te bouwen, maar kun je elke waarde direct berekenen. Maar niet altijd is zo'n directe formule gemakkelijk te vinden.
-
Ligt de gevonden recursieformule toe. Waarom moet je bij een recursieformule ook altijd minstens één term van de rij weten?
-
Laat zien hoe de recursie werkt door met de hand de eerste vier termen van de rij te berekenen. Controleer je antwoorden door op de grafische rekenmachine een tabel te maken bij deze rij.
-
Hier zie je een aantal rijen waarvan de regelmaat is gegeven. Stel telkens zowel een recursieformule als een directe formule op. Nummer de termen steeds vanaf 0.
- De even getallen: 0, 2, 4, 6, 8, ...
- De oneven getallen: 1, 3, 5, 7, 9, ...
- De kwadraten: 1, 4, 9, 16, 25, ...
- De faculteiten: 1, 1, 2, 6, 24, 120, ...
Verwerken
-
Bekijk de rij 2, 5, 8, 11, 14, ... (elke term is 3 groter dan de voorgaande term).
- Schrijf de volgende vijf termen op.
- Beschrijf de rij met een directe formule.
- Beschrijf de rij met een recursieformule.
-
Bekijk de rij 2, 6, 18, 54, 162, ... (elke term is 3 maal de voorgaande term).
- Schrijf de tiende term op.
- Beschrijf de rij met een directe formule.
- Beschrijf de rij met een recursieformule.
-
A en B huren elk een winkelpand voor € 20.000 per jaar. De huur voor A wordt
jaarlijks verhoogd met € 1000, die van B wordt jaarlijks verhoogd met 4%.
- Stel een formule op voor de huur `a_n` van A in jaar `n` (nummer de jaren met 0, 1, 2, ...).
- Stel een formule op voor de huur `b_n` van B in jaar `n` (nummer de jaren met 0, 1, 2, ...).
- Na hoeveel jaren wordt de huur van B groter dan die van A?
B nummert de jaren toch liever met 1, 2, 3, ...
- Hoe luidt dan de formule voor zijn huur?
A betrekt zijn pand in 2003 en wil de jaren nummeren met 2003, 2004, 2005, ...
- Hoe luidt dan de formule voor zijn huur?
-
Hieronder staat van een aantal rijen het begin. Het vervolg raad je zelf wel. Stel
voor elke rij een mogelijke directe formule op. Begin de nummering met 0.
- `1, 1/2, 1/3, 1/4, 1/5, 1/6, ...`
- `6, 11, 16, 21, ...`
- `1, -2, 4, -8, 16, -32, ...`
- `1/4, 1/2, 1, 2, 4, 8, ...`
- `1024, 512, 256, 128, 64, 32, ...`
- `2, 3/2, 4/3, 5/4, 6/5, ...`
- `13, 8, 3, -2, -7, ...`
- `1, 1/4, 1/9, 1/16 , 1/25 , ...`
-
Stel recursieformules op voor de rijen bij b, c, d, e en g van de vorige opgave.
-
De rij `t_0, t_1, t_2, ...` is gegeven door de directe formule `t_n = n^2 + n`.
- Schrijf de eerste 10 termen op.
- Bepaal de kleinste `n` waarvoor `t_n > 1000`.
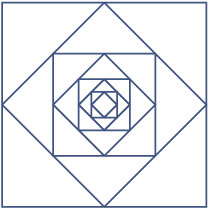 Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
- Hoe lang zijn de zijden van `V_5` en hoe groot is de oppervlakte van `V_5`?
- Stel een directe formule op voor `Z(n)` en voor `O(n)`.
- Stel een recursieformule op voor `Z(n)` en voor `O(n)`.
- Breng de rij `O(0),O(1),O(2), ...` met de grafische rekenmachine in beeld. Kun je daarmee bepalen voor welke `n` `O(n)` (in theorie) kleiner wordt dan 1 mm2? Zo nee, probeer een andere manier.
Testen
-
De rij `t_0, t_1, t_2, ...` is gegeven door de directe formule `t_n = 1 + 2n`.
- Schrijf de eerste twaalf termen op.
- Wat is de 100-ste term?
- Aan welke recursieformule voldoet deze rij?
- Geef de eerste zes termen van een andere rij die aan dezelfde recursie voldoet.
-
De rij `u(0), u(1), u(2), ...` is gegeven door `u(n) = 10 + 1/2 n(n + 1)`.
- Schrijf de eerste tien termen op.
- Gebruik de grafische rekenmachine om de kleinste `n` te vinden waarvoor geldt: `u(n) > 10^6`.
-
Bij de volgende beginstukken van rijen ligt het vervolg voor de hand. Geef bij elk
geval een directe en een recursieformule bij nummering vanaf 0.
- `4, 8, 12, 16, 20, ...`
- `3, 1, 1/3, 1/9, 1/27 , ...`
- `1, -2, 4, -8, 16, -32, ...`
- `3/2, 1, 1/2, 0, -1/2, -1, ...`












 Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.