
Rijen beschrijven
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Uitleg
Opgaven
-
Bekijk het verhaal van het huren van een kamer in de Uitleg. Neem aan dat de jaarlijkse huurverhoging 60 euro is.
- Maak eerst zelf een tabel met huurprijzen voor `n = 0,1,2,3,4,...`
- Hoe heb je jouw tabel gemaakt: met behulp van recursie of door direct de prijzen te berekenen?
- Ligt zowel de formule bij de directe berekening als die bij de recursie toe. Leg duidelijk het verschil tussen beide uit.
-
Bij het verhaal in de Uitleg is ook sprake van een jaarlijkse huurverhoging van 2%.
- Maak ook hiervoor een tabel met huurprijzen voor `n = 0,1,2,3,4,...`
- Hoe heb je jouw tabel gemaakt: met behulp van recursie of door direct de prijzen te berekenen?
- Stel een formule op voor het berekenen van de huurprijs `h_2` door middel van recursie.
- Stel ook een formule op voor `h_2(n)` waarmee je de huurprijs van jaar `n` direct kunt berekenen.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
Bekijk Voorbeeld 1.
- Waarom zijn de twee gegeven formules directe formules?
- Maak tabellen bij beide formules op je grafische rekenmachine in de functie-mode.
- Maak ook tabellen bij beide formules op je grafische rekenmachine in de rijen-mode. Doe eventueel eerst het Practicum.
- Ga na, dat tot `n = 6` de huurverhoging in procenten het gunstigst is.
-
Bekijk Voorbeeld 2.
- Waarom zijn de twee gegeven formules recursieformules?
- Maak tabellen bij beide formules op je grafische rekenmachine in de rijen-mode. Bekijk eventueel het Practicum nog eens.
- Maak grafieken bij beide rijen.
- Ga na, dat tot `n = 6` de huurverhoging in procenten het gunstigst is.
-
In Voorbeeld 3 wordt bekeken hoe je bij een rij een formule kunt maken. Een directe formule is altijd het handigst, dan hoef je de rij niet vanaf het begin op te bouwen, maar kun je elke waarde direct berekenen. Maar niet altijd is zo'n directe formule gemakkelijk te vinden.
-
Ligt de gevonden recursieformule toe. Waarom moet je bij een recursieformule ook altijd minstens één term van de rij weten?
-
Laat zien hoe de recursie werkt door met de hand de eerste vier termen van de rij te berekenen. Controleer je antwoorden door op de grafische rekenmachine een tabel te maken bij deze rij.
-
Hier zie je een aantal rijen waarvan de regelmaat is gegeven. Stel telkens zowel een recursieformule als een directe formule op. Nummer de termen steeds vanaf 0.
- De even getallen: 0, 2, 4, 6, 8, ...
- De oneven getallen: 1, 3, 5, 7, 9, ...
- De kwadraten: 1, 4, 9, 16, 25, ...
- De derde machten: 1, 8, 27, 64, 125, ...
Verwerken
-
Bekijk de rij 2, 5, 8, 11, 14, ... (elke term is 3 groter dan de voorgaande term).
- Schrijf de volgende vijf termen op.
- Beschrijf de rij met een directe formule.
- Beschrijf de rij met een recursieformule.
-
Bekijk de rij 2, 6, 18, 54, 162, ... (elke term is 3 maal de voorgaande term).
- Schrijf de tiende term op.
- Beschrijf de rij met een directe formule.
- Beschrijf de rij met een recursieformule.
-
A en B huren elk een winkelpand voor € 20.000 per jaar. De huur voor A wordt
jaarlijks verhoogd met € 1000, die van B wordt jaarlijks verhoogd met 4%.
- Stel een formule op voor de huur `a_n` van A in jaar `n` (nummer de jaren met 0, 1, 2, ...).
- Stel een formule op voor de huur `b_n` van B in jaar `n` (nummer de jaren met 0, 1, 2, ...).
- Na hoeveel jaren wordt de huur van B groter dan die van A?
B nummert de jaren toch liever met 1, 2, 3, ...
- Hoe luidt dan de formule voor zijn huur?
A betrekt zijn pand in 2003 en wil de jaren nummeren met 2003, 2004, 2005, ...
- Hoe luidt dan de formule voor zijn huur?
-
Hieronder staat van een aantal rijen het begin. Het vervolg raad je zelf wel. Stel
voor elke rij een mogelijke directe formule op. Begin de nummering met 0.
- `1, 1/2, 1/3, 1/4, 1/5, 1/6, ...`
- `6, 11, 16, 21, ...`
- `1, -2, 4, -8, 16, -32, ...`
- `1/4, 1/2, 1, 2, 4, 8, ...`
- `1024, 512, 256, 128, 64, 32, ...`
- `2, 3/2, 4/3, 5/4, 6/5, ...`
- `13, 8, 3, -2, -7, ...`
- `1, 1/4, 1/9, 1/16 , 1/25 , ...`
-
Stel recursieformules op voor de rijen bij b, c, d, e en g van de vorige opgave.
-
De rij `t_0, t_1, t_2, ...` is gegeven door de directe formule `t_n = n^2 + n`.
- Schrijf de eerste 10 termen op.
- Bepaal de kleinste `n` waarvoor `t_n > 1000`.
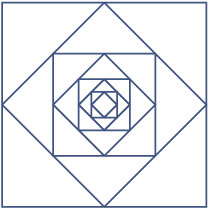 Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
- Hoe lang zijn de zijden van `V_5` en hoe groot is de oppervlakte van `V_5`?
- Stel een directe formule op voor `Z(n)` en voor `O(n)`.
- Stel een recursieformule op voor `Z(n)` en voor `O(n)`.
- Breng de rij `O(0),O(1),O(2), ...` met de grafische rekenmachine in beeld. Kun je daarmee bepalen voor welke `n` `O(n)` (in theorie) kleiner wordt dan 1 mm2? Zo nee, probeer een andere manier.
Testen
-
De rij `t_0, t_1, t_2, ...` is gegeven door de directe formule `t_n = 1 + 2n`.
- Schrijf de eerste twaalf termen op.
- Wat is de 100-ste term?
- Aan welke recursieformule voldoet deze rij?
- Geef de eerste zes termen van een andere rij die aan dezelfde recursie voldoet.
-
De rij `u(0), u(1), u(2), ...` is gegeven door `u(n) = 10 + 1/2 n(n + 1)`.
- Schrijf de eerste tien termen op.
- Gebruik de grafische rekenmachine om de kleinste `n` te vinden waarvoor geldt: `u(n) > 10^6`.
-
Bij de volgende beginstukken van rijen ligt het vervolg voor de hand. Geef bij elk
geval een directe en een recursieformule bij nummering vanaf 0.
- `4, 8, 12, 16, 20, ...`
- `3, 1, 1/3, 1/9, 1/27 , ...`
- `1, -2, 4, -8, 16, -32, ...`
- `3/2, 1, 1/2, 0, -1/2, -1, ...`

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Discrete wiskunde > Rijen > Rijen beschrijven > Theorie Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.
Bij een vierkant `V_0` met zijden van 1 meter zijn de middens van de zijden de
hoekpunten van een kleiner vierkant `V_1`. Net zo maak je `V_2` bij `V_1`, enzovoort.
Laat `O(n)` de oppervlakte van `V_n` in m2 zijn en `Z(n)` de lengte van zijn zijde in m.