Veeltermen

Inleiding

Alle kwadratische functies hebben dezelfde vorm grafiek als de functie `f(x) = x^2`. Je kunt je ook wel functies voorstellen die bestaan uit een optelling van machtsfuncties met hogere machten, zoals bijvoorbeeld `g(x) = x^3 - 4x` of `h(x) = 0,5x^4 + 8x^2 + 5`.
Dergelijke functies heten veeltermfuncties, want het functievoorschrift is een veelterm (of polynoom).
En je kunt je afvragen hoe het zit met hun grafieken...

Je leert nu:

Je kunt al:

Verkennen

Bekijk de grafiek van de veelfunctie `g` met functievoorschrift `g(x) = x^3 - 4x`.

> Welke karakteristieken heeft de grafiek van `g`?
> Schrijf domein en bereik van `g` op.
> Waarom is het geen machtsfunctie?

Uitleg

De functie `f(x) = -x^3 - 4x^2 + 12x` is een voorbeeld van een veeltermfunctie. Elke uitdrukking die bestaat uit een optelling of aftrekking van machtsfuncties met een gehele positieve exponent en eventueel een constant getal, heet namelijk een veelterm (of polynoom).

Om de grafiek goed in beeld te krijgen, wil je vooraf weten hoeveel nulpunten en toppen er zijn. Daarover hebben wiskundigen zich uiteraard gebogen en het is bewezen dat het maximaal aantal nulpunten gelijk is aan de grootste exponent. In dit geval zijn er maximaal drie nulpunten. Die drie nulpunten kun je in dit geval algebraïsch berekenen:

 `-x^3 - 4x^2 + 12x = 0`

`-x(x^2 + 4x - 12) = 0`

 `-x(x + 6)(x - 2) = 0`

`x = 0 vv x = -6 vv x = 2`

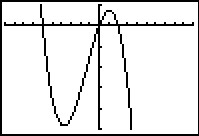
De enige nulpunten zijn `(-6,0), (0,0)` en `(2,0)`.
Het aantal toppen is nu ook wel te beredeneren: voor hele grote (negatieve) waarden van `x` lijkt de grafiek op de machtsfunctie `y = -x^3`. Omdat die machtsfunctie geen toppen heeft zijn de twee toppen tussen de drie nulpunten ook de enige twee.
De grafiek wordt zoals hiernaast met een venster van `[-10,10]` bij `[-50,10]`.

‡

Opgaven

  1. Bekijk de Uitleg.
    1. Bepaal met de grafische rekenmachine beide toppen van de grafiek in twee decimalen nauwkeurig.
    2. Bereken de exacte snijpunten van de grafiek van `f` met de parabool `y = -4x^2`.

  2. Neem de kwadratische functie `g` met `g(x) = 0,5x^4 - 8x^2`.
    1. Bereken algebraïsch de drie nulpunten van deze functie.
    2. Bereken de toppen van de grafiek van `g` met de grafische rekenmachine. (`x`-waarden in twee decimalen nauwkeurig.)
    3. Los op `f(x) < 4 - x^2`.

Theorie

Een veeltermfunctie is een functie die bestaat uit een optelling (of aftrekking) van machtsfuncties met gehele exponenten groter of gelijk 0.
Een voorbeeld uis:
f(x) = ax4 + bx3 + cx2 + dx + e,
waarin a, b, c, d en e constanten zijn.
Zolang a ≠ 0 krijg je een vierdegraads functie.
Als a = 0 en b ≠ 0 krijg je een derdegraads functie.
Enzovoort...

Als je wat experimenteert met je grafische rekenmachine zul je ontdekken dat een vierdegraads functie maximaal vier nulpunten en maximaal drie toppen heeft.
En zo heeft een derdegraads functie maximaal drie nulpunten en twee toppen.
Een vergelijkbare regelmaat geldt voor elke veelterm...

‡

Voorbeeld 1

Gegeven is de functie f met f(x) = –0,5x4 + 800x2.
Hoeveel toppen heeft deze functie?

Antwoord

Om te kunnen vaststellen hoeveel toppen er zijn breng je de grafiek van f met alle karakteristieken in beeld. Het is handig om eerst de nulpunten te berekenen:

–0,5x4 + 800x2 = 0

–0,5x2(x2 – 1600) = 0

x2 = 0  V  x2 = 1600

x = 0  V  x = –40  V  x = 40.

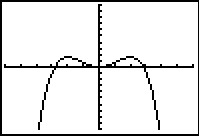
Er zijn drie nulpunten (eigenlijk vier, er vallen twee samen met x = 0 en x = –0), te weten: (0, 0), (–40, 0) en (40, 0).
De grafiek komt met alle karakteristieken in beeld met een venster van [–60,60] bij [–1000000,1000000].
Er zijn drie toppen die je door de rekenmachine kunt laten bepalen.

‡

Voorbeeld 2

Los op: –0,5x4 + 800x > 50000.
(Benaderingen in twee decimalen nauwkeurig.)

Antwoord

Eerst breng je y1 = –0,5x4 + 800x en y2 = 50000 goed in beeld. Zorg er voor dat alle snijpunten zichtbaar zijn.
De grafiek van y1 is die van functie f uit Voorbeeld 1. Ga nog even na hoe je die grafiek goed in beeld krijgt.

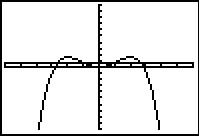
Nu laat je de GR alle nulwaarden bepalen.
Je vindt: `x ~~ -27,05 vv x ~~ -8,27 vv x ~~ 8,27 vv x ~~ 27,05`.

De oplossing van de ongelijkheid wordt: `-27,04 <= x <= -8,27 vv 8,27 <= x <= 27,04`.

‡

Voorbeeld 3

Een landbouwer verbouwt bieten. Bieten moet je vrij houden van onkruid, dat heet "wieden". Hoe meer mensen gaan wieden, hoe beter de bieten groeien. Maar als er weer te veel mensen gaan wieden lopen ze elkaar in de weg en vertrappen ze de bietenplantjes zelf. De oogst Q (in honderden kg bieten) hangt af van het aantal werkers w volgens de formule Q = –0,5w3 + 9w2.
Hoeveel bietenwieders kan deze landbouwer het beste inzetten?

Antwoord

Bekijk eerst de grafiek van deze functie.
Omdat Q niet negatief kan zijn en de nulwaarden w = 0 en w = 18 zijn, heeft de functie Q(w) als domein [0, 18]. De grafiek ziet er zo uit met een venster van [0,18] bij [0,500].

Op de vraag zijn twee antwoorden mogelijk:

‡

Opgaven

  1. Bestudeer de Theorie. Derdegraads functies hebben de vorm `f(x) = ax^3 + bx^2 + cx + d` met `a != 0`.
    1. Neem `a=1, b=0, c=0` en `d=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    2. Neem `a=1, b=4, c=0` en `d=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    3. Neem `a=1, b=0, c=4` en `d=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    4. Neem `a=1, b=0, c=-4` en `d=0`. Hoeveel nulpunten heeft `f` dan? En hoeveel toppen?
    5. Hoeveel nulpunten en hoeveel toppen heeft een derdegraads functie maximaal?

  2. Bekijk de vierdegraads functie `f(x) = 2x^4 - 512x^2`. Je wilt de nulpunten en de toppen van de grafiek van `f` bepalen. Bekijk Voorbeeld 1.
    1. Bereken de exacte nulpunten van `f`.
    2. Bij welke vensterinstellingen krijg je nu de grafiek van `f` goed in beeld?
    3. Hoeveel toppen zijn er? Bepaal de extremen van `f` in één decimaal nauwkeurig.

  3. Je wilt de ongelijkheid `0,5x^4 - 60x^2 < x^2 - 200` oplossen. Bekijk eventueel Voorbeeld 2.
    1. Eerst breng je de grafieken goed in beeld. Bereken daartoe de nulpunten van `y_1 = 0,5x^4 - 60x^2` en die van `y_2 = x^2 - 200`.
    2. Los `y_1 = y_2` op met de grafische rekenmachine en geef de oplossing van de ongelijkheid in één decimaal nauwkeurig.

  4. In Voorbeeld 3 zie je een praktijkvoorbeeld waarin een derdegraads functie voorkomt.
    1. Breng zelf de grafiek in beeld.
    2. Licht de mogelijke antwoorden op de vraag met behulp van de grafiek en de bijpassende tabel toe.

Verwerken

  1. Gegeven de functie `f` met `f(x) = (x^2 - 4)^2 - 100`.
    1. Laat zien dat hier sprake is van een vierdegraads functie.
    2. Bereken algebraïsch de nulpunten van de grafiek van `f`.
    3. Bereken de extremen van `f`.
    4. Los algebraïsch op: `f(x) <= -91`.

  2. Los de volgende vergelijkingen en ongelijkheden algebraïsch op:
    1. `x^3 - 4x^2 = 21x`
    2. `x(x^3 - 1) <= 7x`
    3. `x(6 - x)(x + 5) >= 0`
    4. `2x^4 - 12x = -18x`
    5. `x^4 - 7x^3 + 10x^2 = 0`
    6. `60 - 0,5x^4 >= 0`

  3. ChemTech produceert een bepaald onkruidbestrijdingsmiddel. Voor de productiekosten per maand gelden deze gegevens:

    `q` (in duizenden kg per maand)123456
    `TK` (in euro per maand)77510001220200040008000

    Hierin is `q` de geproduceerde hoeveelheid per maand in duizenden kg en is `TK` de totale kosten in euro. Verder verkoopt ChemTech dit middel voor € 2,25 per kg.
    1. De bedrijfsleiding heeft voor de kostenfunctie deze formule bedacht `TK = 100q^3 - 600q^2 + 1300q`. Laat zien dat deze formule redelijk goed bij de gegeven tabel past.
    2. Stel een formule op voor de totale winst `TW` afhankelijk van `q`. Ga er van uit dat de geproduceerde hoeveelheid elke maand ook wordt verkocht.
    3. Bepaal met de grafische rekenmachine bij welke productie per maand de winst maximaal is.

Testen

  1. Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
    1. `x^4 - 8x >= 0`
    2. `-x^2(x - 5) = 2x^2`
    3. `20 - x^4 = 11`
    4. `(x^2 - 4)(x^2 - 9) < 36`

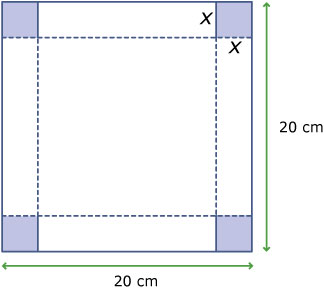  2. Je maakt een bakje met een open bovenkant door van een vierkant stuk karton van 20 cm bij 20 cm de vier hoeken in te knippen en als plakstroken te gebruiken. De ingeknipte hoeken zijn vierkantjes van `x` cm bij `x cm`.
    Er ontstaan zo een bakje met een hoogte van `x` cm.
    1. Welke afmetingen heeft de bodem van het bakje nu?
    2. Stel een formule op voor de inhoud `I(x)` van dit bakje.
      (Hoewel de bovenkant open is moet je er van uit gaan van er niets boven het bovenvlak uitsteekt!)
    3. Voor welke waarden van `x` is de inhoud van het bakje groter dan 500 cm3?