De abc-formule

Inleiding

In het vorige onderdeel heb je gezien hoe je de vergelijking 2(x – 1)² – 5 = 3 oplost door terug te rekenen. Dat terugrekenen lukt omdat de x maar op één plaats in de vergelijking voorkomt.
Kwadratische vergelijkingen komen ook voor in een vorm waarin terugrekenen niet mogelijk is. Werk je namelijk de haakjes weg, dan krijg je 2x² – 4x – 3 = 3.
De x komt nu op meer plekken voor en terugrekenen is niet meer mogelijk. Door kwadraatafsplitsen kun je ook een formule afleiden waarmee een dergelijke vergelijking in één keer op te lossen is. Dat is de zogenaamde abc-formule.

Je leert nu:

• nagaan hoeveel oplossingen een kwadratische vergelijking van de vorm ax² + bx + c = 0 heeft;
• kwadratische vergelijkingen van de vorm ax² + bx + c = 0 oplossen.

Je kunt al:

• kwadratische vergelijkingen van de vorm a(x – p)² + q = u oplossen.

Verkennen

Bekijk de grafiek van de functie g(x) = 2(x + 1)² + 7 .

> Schrijf het functievoorschrift van g in de vorm g(x) = ax² + bx + c.
> Hoe kun je met de grafische rekenmachine nagaan of je dit goed hebt gedaan?
> Hoe kun je aan een functievoorschrift van de vorm g(x) = ax² + bx + c zien of de grafiek een dal- of een bergparabool is?
> Hoe bepaal je de top van de grafiek van g?

Bekijk vervolgens de grafiek van f(x) = x² + 6x – 8.

> Hoe bepaal je nu algebraïsch de top en de nulpunten van de grafiek van f?

Uitleg

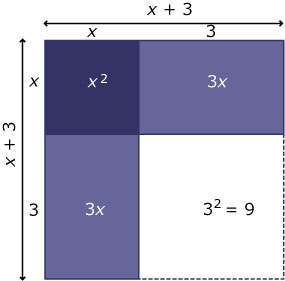
De vergelijkng x² + 6x = 16 kun je niet oplossen door terugrekenen. Maar... bekijk de figuur hiernaast eens.
Zie je dat x² + 6x = (x + 3)² – 3²?
Dit betekent dat je de gegeven vergelijking kunt schrijven als: (x + 3)² – 9 = 16.
En nu komt x weer op één plek voor en kun je terug rekenen:

(x + 3)² – 9 = 16                  _{beide zijden 9 optellen}
      (x + 3)² = 25                   _{worteltrekken}
   x + 3 = 5  V  x + 3 = –5    _{3 aftrekken}
         x = 2  V  x = –8

Op dezelfde manier kun je ook bijvoorbeeld de vergelijking 3x² + 17x = 45 oplossen.
Je deelt dan eerst door 3, probeer maar...
Omdat dit een tijdrovend gepruts is hebben wiskundigen de oplossingen berekend voor het algemene geval. Dat gaat ook met kwadraat afsplitsen. Je krijgt het volgende resultaat:

De vergelijking ax² + bx + c = 0 heeft als oplossing:

`x = (-b + sqrt(b^2 - 4ac))/(2a) vv x = (-b - sqrt(b^2 - 4ac))/(2a)`

Dit noem je de abc-formule of wortelformule.
Deze formule geeft meteen de twee oplossingen als je de juiste waarden voor a, b en c invult. De vergelijking moet vaak wel eerst nog in de vorm ax² + bx + c = 0 worden gezet!

Ga na, dat de oplossing van 3x² + 17x = 45, en dus 3x² + 17x – 45 = 0 is:
`x = (-17 + sqrt(829))/6 vv x = (-17 - sqrt(829))/6`.
De uitdrukking b² – 4ac onder het wortelteken heet de discriminant. Omdat die discriminant in dit geval 829 is zijn er twee mogelijke antwoorden. Is de discriminant negatief, dan zijn er geen reële oplossingen. Je kunt die discriminant beter eerst uitrekenen.

‡

Opgaven

1. Gegeven is de kwadratische functie `f` met functievoorschrift `f(x) = x^2 + 6x + 1`. Je wilt de nulpunten van `f` berekenen.
   1. In de Uitleg, pagina 1 kun je zien hoe dat in zijn werk gaat. Leg uit waarom `x^2 + 6x = (x + 3)^2 - 9`.
   2. Bereken algebraïsch de nulpunten van de grafiek van `f` in twee decimalen nauwkeurig.
   3. Je kunt deze nulpunten ook vinden met de `abc`-formule, zie de Uitleg, pagina 2. Bepaal de nulpunten nog eens, maar nu met de `abc`-formule.
   4. Welke top heeft de grafiek van `f`?


2. Neem de kwadratische functie `g` met `g(x) = x^2 + 8x + 3`. Je wilt weer de nulpunten berekenen.
   1. Laat zien dat `g(x) = (x + 4)^2 - 13`.
   2. Bepaal nu exact de beide nulpunten.
   3. Welke top heeft de grafiek van `g`?
   4. Bepaal beide nulpunten ook met behulp van de `abc`-formule. Laat zien dat je dezelfde nulpunten vindt dan bij b.
   5. Wat is het nadeel van het gebruik van de `abc`-formule?


3. De vergelijking `2x^2 + 8x = 24` kun je op meerdere manieren oplossen.
   1. Los deze vergelijking op door ontbinden in factoren.
   2. Je kunt deze vergelijking ook oplossen door hem te schrijven als `(x - 2)^2 = 16`. Laat zien hoe dat gaat en los hem dan verder op.
   3. Tenslotte kun je deze vergelijking oplossen met de `abc`-formule. Doe dat ook nog een keer.
   4. Welke methode vind je het handigst en waarom?

Theorie

Een algemene vorm voor een kwadratische functie is
f(x) = ax² + bx + c.
Wil jede nulpunten van de bijbehorende parabool vinden, dan moet je oplossen `ax^2 + bx + c = 0`.

Wiskundigen hebben al lang geleden de abc-formule afgeleid.
Daarmee kun je de vergelijking ax² + bx + c = 0 oplossen en zo de nulpunten van de kwadratische functie berekenen. De gevonden oplossing is:

`x = (-b + sqrt(b^2 - 4ac))/(2a) vv x = (-b - sqrt(b^2 - 4ac))/(2a)`

De uitdrukking D = b² – 4ac die onder het wortelteken staat heet de discriminant van de kwadratische vergelijking. Omdat alleen de wortel uit een positief getal of 0 een reëel getal oplevert, bepaalt die discriminant het aantal oplossingen van de vergelijking:

• D > 0 en er zijn twee oplossingen;
• D = 0 en er is één oplossing (twee dezelfde);
• D < 0 en er zijn geen reële oplossingen;

‡

Voorbeeld 1

Los op: x² + 10x = 15.

Antwoord

Terugrekenen kan niet, maar op x² + 10x kun je kwadraat afsplitsen toepassen:
x² + 10x = (x + 5)² – 25.

Je past nu de abc-formule toe.
Eerst schrijf je de vergelijking als: x² + 10x – 15 = 0.
Dan neem je a = 1, b = 10 en c = –15.
Discriminant: D = b² – 4ac = 100 – 4 · 1 · – 15 = 160.
De discriminant is positief, er zijn twee oplossingen: `x = (-10 + sqrt(160))/(2) vv x = (-10 - sqrt(160))/(2)`
Je kunt beide oplossingsmethoden benaderen in het gewenste aantal decimalen.

‡

Voorbeeld 2

Bepaal algebraïsch de nulpunten van de functie
`f(x) = 2x^2 - 2x - 4`.

Antwoord

Je kunt meteen oplossen: `2x^2 - 2x - 4 = 0`.
Dat kun je doen met behulp van de abc-formule, maar nog veel sneller door ontbinden in factoren toe te passen:

`2x^2 - 2x - 4 = 2(x^2 - x - 2) = 2(x - 2)(x + 1)`.

De nulpunten vind je uit `2(x - 2)(x + 1) = 0`.
Dus je krijgt `(2,0)` en `(-1,0)`.
De symmetrieas ligt midden tussen beide nulpunten in, dus de top van de parabool kun je nu ook gemakkelijk bepalen.

‡

Voorbeeld 3

Los op: –2x² < 8 – x.

Antwoord

De bijbehorende vergelijking herschrijf je eerst tot: –2x² + x – 8 = 0.
Je ziet dan dat: a = –2, b = 1 en c = –8.
Discriminant: D = b² – 4ac = –63.
De discriminant is negatief, dus de vergelijking heeft geen reële oplossingen.

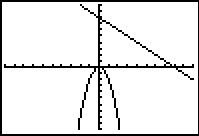
Nu bekijk je de grafieken van y₁ = –2x² en y₂ = 8 – x. En dan denk je: "Waarom heb ik dit niet eerder gedaan?" want je ziet meteen dat er geen snijpunten zijn: y₁ is voor elke x kleiner dan y₂.

Antwoord: elke reële x-waarde is oplossing van deze ongelijkheid.

‡

Opgaven

4. Bestudeer Voorbeeld 1. Je gaat nu zelf de vergelijking `x^2 + 12x = 30` oplossen.
   1. Doe dit eerst door de vergelijking te schrijven als `(x + 6)^2 = 66`.
   2. Doe dit vervolgens nog eens met de `abc`-formule.


5. Bekijk de kwadratische functie `f(x) = 2x^2 - 6x + 2`. Je wilt de nulpunten (in twee decimalen nauwkeurig) en de top van de grafiek van `f` bepalen. Bekijk Voorbeeld 2.
   1. Probeer dit eerst met behulp van kwadraat afsplitsen.
   2. Je kunt de nulpunten ook meteen met de `abc`-formule berekenen. Bepaal wat dan de `a`, `b` en `c` zijn. Bereken daarna de discriminant.
   3. Kun je aan de discriminant zien hoeveel oplossingen de vergelijking `f(x)=0` heeft?
   4. Los de vergelijking `f(x)=0` op en ga na dat je zo dezelfde nulpunten vindt als bij a.
   5. Werk je met de `abc`-formule, dan moet je vanuit de nulpunten de top bepalen. Hoe gaat dat in zijn werk?


6. Je wilt de ongelijkheid `3x^2 + 6x < x + 8` oplossen. Als je de `abc`-formule wilt gebruiken om een vergelijking op te lossen, moet de vergelijking in de vorm `ax^2 + bx + c = 0` staan. Bekijk Voorbeeld 3.
   1. Schrijf de bij de ongelijkheid horende vergelijking `3x^2 + 6x = x + 8` in deze vorm en bereken de oplossingen met de `abc`-formule.
   2. Controleer de oplossingen met de grafische rekenmachine en geef de oplossing van de ongelijkheid.


7. Kwadratische vergelijkingen kunnen soms ook opgelost worden door ontbinden in factoren. Ga bij elk van de volgende vergelijkingen na of ze opgelost kunnen worden met ontbinden in factoren. Bereken van elk van de vergelijkingen de oplossing. Gebruik de `abc`-formule alleen als dat echt nodig is.
   1. `x^2 - x - 3 = 0`
   2. `-4x^2 + 5x - 14=0`
   3. `2x^2 - 10x + 10 = 2x - 6`
   4. `x - 5x^2 = 10`
   5. `x(x - 7) = 8`

Verwerken

8. Gegeven de kwadratische functie `f` met `f(x) = x^2 + 8x - 20`.
   1. Schrijf het functievoorschrift in een zodanige vorm dat je de top van de grafiek eruit kunt aflezen.
   2. Je kunt nu op drie manieren de nulpunten van de grafiek van `f` berekenen. Doe dit eerst door het functievoorschrift dat je bij a hebt gevonden te gebruiken
   3. Bereken de nulpunten ook met behulp van de `abc`-formule.
   4. Tenslotte kun je gebruik maken van ontbinden in factoren. Dat gaat verreweg het snelst als je de ontbinding "ziet". Bereken de nulpunten nog eens op deze manier.


9. Teken met de grafische rekenmachine en één figuur de grafieken van `f(x) = 2x^2 - x + 1` en `g(x) = 10 - 3x`.
   1. Los op: `f(x) = g(x)`
   2. Los in drie decimalen nauwkeurig op: `f(x) > g(x)`


10. Los de volgende vergelijkingen op:
    1. `x^2 + 3x + 13 = 0`
    2. `1/3x^2 + 10x + 1 = 0`
    3. `2x^2 - 5x = x`
    4. `2x^2 - 12x = -18`
    5. `x^2 - 5x + 10 = 0`
    6. `x(x - 1) = 12`
    7. `60 - x^2 = 0`
    8. `5 - 1/3x^2 = 1`
    9. `x - 5x^2 = 3`

Testen

11. Los de volgende vergelijkingen en ongelijkheden algebraïsch op.
    1. `x^2 - 2x - 15 = 0`
    2. `-x^2 - x - 1 = 0`
    3. `20 - x^2 = 11`
    4. `x(x + 2) < 14`
    5. `x^2 - x + 10 >= 3`


12. Gegeven zijn de functies `f(x) = 100 - x^2` en `g(x) = 1/2 x^2 - 10x`.
    1. Bereken de nulpunten van de grafieken van `f` en `g`.
    2. Bereken algebraïsche de snijpunten van de twee grafieken van `f` en `g` in twee decimalen nauwkeurig.


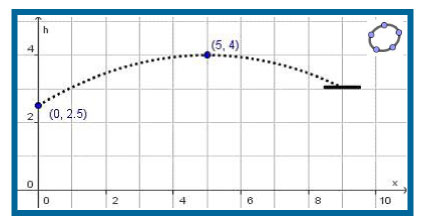
13. Een basketballer maakt een driepunter zonder het bord te raken (hij gooit de bal dus in één keer door de ring van de basket). De baan van de bal is (ongeveer) een parabool, zie figuur. Het hoogste punt van de baan is gegeven. De speler laat de bal op 2,5 m boven de grond los.
    
    
    
    
    1. Stel een formule op voor de functie `h(x)` die de baan van de bal beschrijft.
    2. De ring van de basket hangt op 3,05 m boven de grond. Hoe ver staat de speler vanaf (het midden van) de ring van de basket?