
Exponentiële functies
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Uitleg
Opgaven
-
In de Uitleg wordt gesteld dat je de grafieken van functies van de vorm `f(x) = b * g^x` met de applet kunt bekijken.
-
Neem `b=1` en `g=2`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Welke lijn is de asymptoot van de grafiek van `f`? Is de grafiek stijgend of dalend?
-
Neem `b=1` en `g=3`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Welke lijn is de asymptoot van de grafiek van `f`? Is de grafiek stijgend of dalend?
-
Neem `b=1` en `g=1`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Waarom heeft de grafiek van `f` nu geen asymptoot?
-
Neem `b=1` en `g=0,5`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Welke lijn is de asymptoot van de grafiek van `f`? Is de grafiek stijgend of dalend?
-
Neem `b=2` en `g=1,5`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Welke lijn is de asymptoot van de grafiek van `f`? Is de grafiek stijgend of dalend?
-
Neem `b=-2` en `g=1,5`. Welke functievoorschrift krijg je? Heeft de grafiek van deze functie nulpunten?
Welke lijn is de asymptoot van de grafiek van `f`? Is de grafiek stijgend of dalend?
-
Welke eigenschappen heeft een functie van de vorm `f(x) = b * g^x` als `b < 0`? (Maak ook nu weer verschil tussen `g > 1`, `g = 1` en `0 < g < 1`.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
-
Lees in Voorbeeld 1 over de exponentiële afname van de concentratie van een (verontreinigende) stof in het water van een meer.
-
Leg uit waarom de groeifactor per dag 0,80 is.
-
Breng de grafiek van `C(t)` in beeld op je grafische rekenmachine.
-
Bereken in twee decimalen nauwkeurig vanaf welk tijdstip de concentratie niet meer meetbaar is, dus `C(t) < 1/40`.
-
Bestudeer Voorbeeld 2.
-
Waaraan zie je dat `B` harder groeit dan `A`?
-
Ga na dat je voor het snijpunt van beide grafieken inderdaad `t = 32,6138...` vindt.
-
Een derde stad C is kleiner dan zowel A als B. Maar deze stad groeit heel snel, met 8,3% per jaar.
Op 1-1-2009 is `C` (het aantal inwoners van C) even groot als `B`. Wanneer is `C` even groot als `A`?
-
In Voorbeeld 3 wordt uitgelegd hoe je het functievoorschrift opstelt van een
exponentiële functie als twee punten van de grafiek zijn gegeven.
Stel het voorschrift op van de exponentiële functie `f` waarvan de
grafiek gaat door `(10,200)` en `(14,350)`.
Verwerken
-
Iemand zet € 10000,- op een spaarrekening. De rente is 5% per jaar en wordt
bijgeschreven op de spaarrekening.
-
Stel een bijpassend functievoorschrift op voor het saldo `S(t)` met `t` in jaren na het moment waarop het startbedrag op de spaarrekening is geplaatst. Schrijf op bij welke vensterinstellingen de grafiek goed in beeld komt.
-
Hoe lang duurt het voor het spaartegoed is gegroeid tot € 15000,-?
-
Hoe lang duurt het voor het spaartegoed zich verdubbeld heeft?
-
Een saldo van € 4000,- kan ontstaan zijn doordat ooit iemand € 1,- op een spaarrekening zette tegen 5% rente.
-
Wanneer moet die € 1,- dan op de spaarrekening gezet zijn? Een antwoord tot op een jaar nauwkeurig is voldoende.
-
Kun je dit antwoord ook vinden door een geschikte grafiek van `S(t) = 4000 * 1,05^t` te tekenen?
-
Stel je voor dat je de grafiek van `S` steeds verder naar links door trekt. Zal de grafiek ooit de horizontale as snijden?
Licht je antwoord toe. Wat betekent dit voor de grafiek van `S`?
-
Op een afgelegen terrein wordt op 6-1-2007 een hoeveelheid radioactief afval
gevonden. Aangenomen wordt dat dit afval er al tien jaar heeft gelegen. De
straling blijkt 2000 Bq (becquerel) te zijn. Vier maanden later wordt de straling
opnieuw gemeten. Deze blijkt nu ongeveer 1630 Bq te zijn. De straling neemt exponentieel af.
-
Hoeveel Bq was de straling een jaar geleden? En hoe groot is de straling over 2,5 jaar?
-
Stel een functievoorschrift op voor de hoeveelheid straling, afhankelijk van de tijd `t` in maanden.
Neem `t = 0` op 6-1-2007.
-
Wat is het bereik van de functie bij vraag b?
-
Vanaf welke datum is de straling minder dan 1000 Bq?
-
Persoon A zet op 1-1-2000 € 2000,- op de bank tegen 4% rente per jaar.
Persoon B zet op 1-1-2000 € 1500,- op de bank tegen 6% rente per jaar.
-
Geef de functievoorschrift van het banktegoed `a(t)` van persoon A en het banktegoed `b(t)` van persoon B, waarbij `t` de tijd in jaren is na 1-1-2000.
-
Maak met de grafische rekenmachine de grafieken van de functies `a` en `b`.
Bij welke vensterinstellingen komen de grafieken zo in beeld dat ook het snijpunt zichtbaar is?
-
Vanaf welke maand van welk jaar is het banktegoed van persoon B groter dan dat van persoon A?
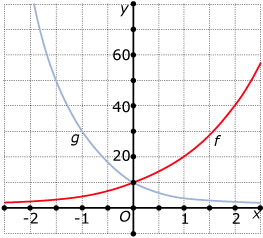 Hier staan de grafieken getekend van
twee exponentiële functies. Geef van
beide functies het functievoorschrift.
Hier staan de grafieken getekend van
twee exponentiële functies. Geef van
beide functies het functievoorschrift.
-
Een huurder betaalt een huur van € 650,- en vindt de jaarlijkse huurverhoging
van 5,5% te veel. Hij herinnert zich nog dat exponentiële groei veel harder gaat
dan lineaire groei. Hij stelt zijn verhuurder daarom voor om de huur elk jaar met
€ 50,- te verhogen. Na hoeveel jaar gaat dit de huurder voordeel opleveren?
Testen
-
Een bepaalde hoeveelheid `H` groeit vanaf `t=0` volgens `H(t) = 200 * 1,03^t`.
-
Hoe zie je aan het functievoorschrift dat er echt van toename sprake is?
-
Vanaf welke waarde van `t` (in drie decimalen nauwkeurig) is de hoeveelheid 200% groter geworden dan op `t=0`?
-
Neem aan dat ook voor `t=0` deze hoeveelheid met 3% per tijdseenheid groeide.
Voor welke waarden van `t` is de hoeveelheid kleiner dan 0,01?
-
Iemand betaalt op 1-1-2000 een huur van € 850,- per maand. Jaarlijks wordt in
januari zijn huur met 5,5% verhoogd.
-
Stel het functievoorschrift op voor de huur per maand `H(t)` afhankelijk van de tijd `t` in jaren na 2000.
-
Vanaf welke datum is de huur hoger dan € 1000,- per maand?
-
De grafiek van een exponentiële functie `f` gaat door de punten `(2,80)` en `(8,200)`.
Stel een bijpassend functievoorschrift op.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Inleiding
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Uitleg
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Exponentiële functies > Exponentiële functies > Theorie
 Hier staan de grafieken getekend van
twee exponentiële functies. Geef van
beide functies het functievoorschrift.
Hier staan de grafieken getekend van
twee exponentiële functies. Geef van
beide functies het functievoorschrift.