
Totaalbeeld
Samenvatten
Je hebt nu het onderwerp Afgeleide functies doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
21: definitie afgeleide — limiet — vergelijking raaklijn
22: differentieerregels — machtsregel voor gehele positieve n — somregel — constante-regel
23: extremen — tekenschema afgeleide
24: buigpunt — tweede afgeleide — buigraaklijn
Activiteitenlijst:
21: afgeleiden bepalen — vergelijking van een raaklijn opstellen
22: afgeleiden bepalen m.b.v. differentieerregels
23: extremen berekenen m.b.v. de afgeleide
24: buigpunten berekenen m.b.v. de tweede afgeleide
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Afgeleide functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Afgeleide functies > Totaalbeeld > Achtergronden
Testen
Opgaven
-
Differentieer de volgende functies:
- `f(x) = 4x^5 - 12x^2 + 60x + 100`
- `E(t) = 1 + t + t^2/2 + t^3/6 + t^4/24`
- `f(x) = (ax + b)^2`
- `GTK(q) = (0,5q^3 + 20q^2 + 60q)/q`
-
Bekijk de grafiek van `f(x) = 2x^3 - x^4` op het interval `[-1,5;2,5]`.
-
De grafiek heeft twee punten waarin de raaklijn horizontaal loopt.
Toon met behulp van differentiëren aan, dat er toch maar één extreme waarde is.
- De grafiek van `f` heeft behalve `(0,0)` nog een buigpunt. Bereken de coördinaten van dat punt.
- Stel de raaklijn op aan de grafiek in het bij b bedoelde buigpunt.
-
Gegeven is de functie `f` met `f(x) = 0,5x^3 - 2x`.
- Bereken de extremen van `f` met behulp van differentiëren.
- Laat zien dat `(0,0)` het buigpunt is van de grafiek van `f`.
-
Stel een vergelijking op van de raaklijn aan de grafiek van `f` in het buigpunt.
-
Een fabriek produceert opvouwbare autopeds voor volwassenen als vervoermiddel in grotere bedrijfshallen. Het bedrijf heeft als enige producent een monopoliepositie. Daarom hangt hun afzet `q` (in duizendtallen) uitsluitend af van de prijs `p` in euro: `q = 12 - 0,1p`. De kosten voor de productie van deze autopeds zijn gegeven door een door de bedrijfswiskundige opgesteld model: `TK = 1,5q^3 - 22,5q^2 + 120q`. Hierin is `TK` gegeven in duizendtallen euro.
- Toon aan dat geldt: `p = 120 - 10q`. Welke waarden kan `q` aannemen?
- Stel een formule op voor de opbrengst `TO` als functie van `q`.
- Stel een formule op voor de winst `TW` als functie van de afzet `q`.
- Bepaal met behulp van differentiëren de prijs van één autoped bij maximale winst.
-
Geef een formule voor de gemiddelde totale kosten `GTK` als functie van `q`.
Bepaal met behulp van differentiëren bij welke afzet `GTK` minimaal is.
-
Gegeven zijn de functies: `f(x) = (x^2 - 4)(2x + 1)` en `g(x) = x^2 - 4`.
-
Bepaal algebraïsch de nulpunten en de toppen van de grafiek van `f`.
-
Los op: `f(x) > g(x)`.
Toepassen
-
Een bedrijf maakt plastic bakjes: bodem en zijvlakken van deze bakjes zijn rechthoeken; de breedte van de bakjes is tweemaal zo groot als de hoogte. Om de bakjes te verstevigen wordt een gebogen metaaldraad met een lengte van 120`cm` aangebracht zoals in de tekeningen is aangegeven.
- Bereken de maximale inhoud die deze bakjes kunnen krijgen.
-
Als het goed is blijkt bij a dat de lengte van het bakje viermaal zo groot is als de hoogte.
Toon aan dat bij elke draadlengte een maximale inhoud ontstaat als de breedte tweemaal de hoogte en de lengte viermaal de hoogte is.
-
ChemoTech
Onder de marginale kosten (de meerkosten) wordt in de economie de extra kosten verstaan die de verkoop van één extra eenheid oplevert. Voor marginale opbrengst en - winst bestaan vergelijkbare definities. Deze marginale kosten zijn bij grote hoeveelheden goed te benaderen door middel van een afgeleide. Lees hierover
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
Bij de productie van een bepaald chemisch onkruidbestrijdingsmiddel heeft de bedrijfsleiding
onderzocht hoeveel kilo bestrijdingsmiddel worden geproduceerd per maand afhankelijk van
het aantal werknemers. Deze tabel in Excel laat dat zien.
Een arbeidsplaats kost gemiddeld € 1500,00 per maand en de kosten voor de apparatuur en de
gebouwen bedragen ongeveer € 30000,00 per maand.
-
Je kunt op basis van deze gegevens een tabel opstellen waarin de totale kosten `TK` per maand (in duizenden euro) afhangen van de hoeveelheid bestrijdingsmiddel q die men maandelijks kan produceren.
Maak die tabel en ga na dat deze functie er bij past: `TK = 0,25q^3 - 3q^2 + 18q + 30`.
-
Laat zien, dat de marginale kosten bij een productie van 4500 kg/mnd goed kunnen worden benaderd door de marginale kosten op `q=4`. Welke economische betekenis hebben deze marginale kosten?
-
Als je de grafiek van de totale kostenfunctie bekijkt, zie je dat ze eerst afnemend stijgen.
Bereken tot welke productieomvang (in kilogram) dat het geval is.
-
Het bedrijf gaat dit onkruidbestrijdingsmiddel op de markt brengen voor een prijs die door de harde concurrentie ongeveer vast ligt op € 18,00 per kilogram. Stel een formule op voor de totale winst `TW` in duizenden euro per maand.
-
Bij welke geproduceerde hoeveelheid maakt het bedrijf winst?
-
Bereken de maximale winst als het bedrijf de geproduceerde hoeveelheid bestrijdingsmiddel ook inderdaad verkoopt.
Stel je voor dat dit bedrijf geen concurrentie zou hebben bij de verkoop van dit onkruidbestrijdingsmiddel.
In dat geval is de vraagprijs afhankelijk van de hoeveelheid die men op de markt
brengt: een lage prijs betekent een flinke verkoop, een hoge prijs een minder goede verkoop.
Neem aan dat geldt: `p = 58,5 - 3q`.
-
Hoe hoog is nu de maximaal bereikbare winst? Is die hoger of lager dan in de voorgaande situatie van een vaste prijs?
Examenopgaven
Kurkentrekkers
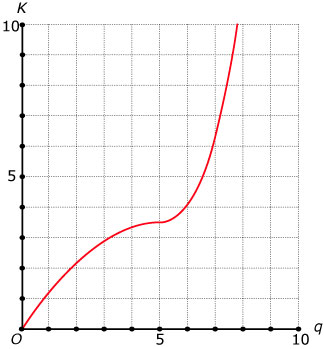
In een bedrijf worden kurkentrekkers gefabriceerd. De totale kosten bij
de productie kun je aflezen in de grafiek. Een wiskundige van het bedrijf
heeft hierbij de volgende formules bedacht:
- `K = -0,1q^2 + 1,2q` als `0 <= q < 5`
- `K = 0,1q^3 - 1,1q^2 + 3,7q` als `q >= 5`
Hierin is `q` de productie (in duizendtallen) en `K` de totale kosten (in duizenden euro).
De toename van de totale kosten bij een toename van de productie met één kurkentrekker noem je de marginale kosten. Deze marginale kosten mogen benaderd worden door `(text(d)K)/(text(d)q)`.
-
Toon door berekening aan dat de marginale kosten bij elke productie positief zijn. Hoe is dit ook uit de grafiek af te leiden?
-
Toon door berekening aan dat de marginale kosten het kleinst zijn voor `q = 5`. Hoe is dit ook uit de grafiek af te leiden?
-
Bereken de gemiddelde totale kosten per kurkentrekker bij een productie van 7000 stuks.
Hoe kun je uit de grafiek afleiden bij welke andere productie de gemiddelde kosten per kurkentrekker even groot zijn als bij een productie van 7000 stuks? Leid deze andere productie uit de grafiek af en controleer het antwoord met de formules.
(bron: examen wiskunde A vwo 1989)
Toltunnel
Het aantal personenauto's (`A`) dat per dag van een nieuw aan te leggen toltunnel gebruik zal
maken, is volgens een verkeersdeskundige te berekenen met de formule
`A = 400T^2 - 9150T + 46800`
Hierbij is `T` het toltarief in euro. Toltarieven hoger dan 7 euro blijven buiten beschouwing. Met
het oog op een snelle doorstroming zal de betaling op electronische wijze geschieden. Hierdoor
is het mogelijk om een toltarief van bijvoorbeeld € 2,67 in rekening te brengen omdat dit niet
op praktische bezwaren stuit.
-
Bereken de totale dagopbrengst aan tolgeld voor personenauto’s bij een toltarief van € 2,00.
-
Onderzoek bij welk toltarief de totale dagopbrengst aan tolgeld voor personenauto's maximaal is.
Geef je antwoord in centen nauwkeurig.
-
Bereken met hoeveel procent het aantal personenauto's afneemt als bij een tarief van € 2,40 een tariefsverhoging van 5% wordt toegepast.
Bij een zeker toltarief leidt een tariefsverhoging van 6% er toe, dat het aantal personenauto’s dat
dagelijks de tunnel gebruikt met 2,8% afneemt.
-
Bereken in gehelen nauwkeurig met hoeveel procent de totale dagopbrengst aan tolgeld voor personenauto's door deze tariefsverhoging zal toenemen.
(bron: examen wiskunde A vwo 1992, aangepast)
Tennis
Bij sporten als volleybal en tennis is de service erg belangrijk, dat wil zeggen de manier waarop de bal in het spel gebracht wordt. We bekijken hier de service bij tennis. De speler staat bij het serveren 12 meter van het net. Het net is 1 meter hoog. We nemen aan dat de speler de bal raakt op een hoogte van 2,5 meter boven de grond en ter vereenvoudiging gaan we er van uit dat de speler de bal precies in de lengterichting van het veld slaat. In de eerste figuur zie je een mogelijke baan van de bal.
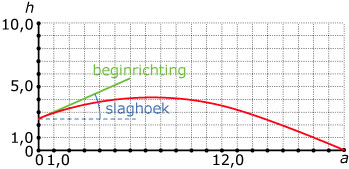
De hoogte van de onderkant van de bal in meter ten opzichte van de grond noemen we `h`. De horizontale afstand in meter noemen we `a`. Het verband tussen `h` en `a` hangt af van de snelheid waarmee de bal geslagen wordt en van de beginrichting. Deze beginrichting wordt bepaald door de slaghoek. Dit is de hoek waaronder de bal geslagen wordt. Zie eerste figuur.
-
Neem aan dat de bal onder een hoek van 15° geslagen wordt met een snelheid van `v` m/s.
Bij deze hoek geldt bij benadering het volgende verband tussen `a` en `h`:
`5,36h = (-5,36)/(v^2) a^2 + 0,27a + 2,50`
Een speler slaat de bal met een snelheid van 17 m/s.
Bereken met behulp van differentiëren de grootste hoogte boven de grond die deze bal bereikt.
In deze vereenvoudigde situatie spreken we van een geldige service als:
- de speler die serveert 12 meter van het net staat;
- de bal precies in de lengterichting van het veld geslagen wordt;
- de bal over het net gaat zonder dit te raken;
- de bal neerkomt op een afstand van ten hoogste 7 meter voorbij het net.
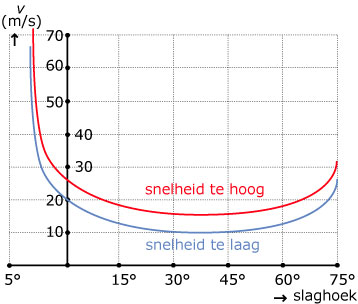 In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
-
Bepaal met behulp van de grafiek de beginrichting van een mogelijke baan van deze bal.
Neem nu aan dat de bal onder een hoek van 10° geslagen wordt. Bij deze hoek geldt bij benadering de volgende formule voor het verband tussen `a` en `h`:
`5,16h = (-5,36)/(v^2) a^2 + 0,18a + 2,50`
Voor een geldige service moet de bal over het net gaan zonder dit te raken. De snelheid is te laag als in bovenstaande formule bij afstand `a=12` de hoogte `h <= 1` is. Volgens de grafiek is een snelheid van 16 m/s of minder te laag voor een geldige service. Echter, met behulp van een berekening is na te gaan dat de figuur hier erg onnauwkeurig is getekend.
-
Welke snelheden (in m/s) zijn volgens de formule te laag voor een geldige service?
Geef je antwoord in ten minste één decimaal nauwkeurig.
Voor een geldige service moet de bal bovendien ten hoogste 7 meter voorbij het net de grond raken. Uit deze eis volgt ook een voorwaarde voor `v`.
-
Welke getallen moet je in de bovenstaande formule invullen om deze voorwaarde te krijgen? Licht je antwoord toe.
(bron: examen wiskunde A vwo 2000, eerste tijdvak)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Afgeleide functies > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Afgeleide functies > Totaalbeeld > Achtergronden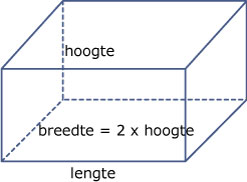

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Afgeleide functies > Totaalbeeld > Toepassen

 In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.
In een artikel over dit onderwerp stond deze grafiek. Daarin is weergegeven bij welke combinaties van slaghoek en snelheid een geldige service verkregenwordt. Een speler die de bal slaat onder een hoek van 30° moet volgens deze grafiek de bal slaan met een snelheid van ongeveer 11 tot 13 m/s. Slaat hij te zacht dan komt de bal niet over het net. Slaat hij te hard dan komt de bal te ver voorbij het net op de grond. Een profspeler slaat bij een geldige service de bal met een snelheid van 150 km/h.