Totaalbeeld

Antwoorden bij de opgaven

1. 1. `f'(x) = 20x^4 - 24x + 60`
   2. `E'(t) = 1 + t + 1/2 t^2 + 1/6 t^3`
   3. `f(x) = a^2x^2 + 2abx + b^2` geeft `f'(x) = 2a^2x + 2ab`
   4. `GTK(q) = 0,5q^2 - 20q + 60` geeft `(text(d)GTK)/(text(d)q) = q - 20`
2. 1. `f'(x) = 6x^2 - 4x^3 = 0` geeft `x=0 vv x=1,5`.
      Aan de grafiek zie je dat er in `(0,0)` wel een horizontale raaklijn maar geen extreme waarde is. De enige extreme waarde is bij `x=1,5`.
   2. `f''(x) = 12x - 12x^2 = 0` geeft `x=0 vv x = 1`. Dus `(1,1)`.
   3. `f'(1) = 2` en dus is de buigraaklijn `y = 2x - 1`.
3. 1. `f'(x) = 1,5x^2 - 2 = 0` geeft `x = +-sqrt(4/3)`. Max.`f(-sqrt(4/3)) = 1 1/3 sqrt(4/3)` en min.`f(sqrt(4/3)) = -1 1/3 sqrt(4/3)`.
   2. `f''(x) = 3x = 0` geeft `x = 0`. Buigpunt: `(0,0)`.
   3. `f('0) = -2` dus raaklijn `y = -2x`.
4. 1. Gegeven vergelijking herschrijven.
      `0 <= q <= 12`
   2. `TO = pq = 120q - 10q^2`
   3. `TW = TO - TK = -1,5q^3 + 12,5q^2`
   4. `TW'(q) = -4,5q^2 + 25q = 0` geeft `q=0 vv q = 50/9`.
      `TW` is maximaal bij `q = 50/9` en dan is `p ~~ 64,44` euro.
   5. `GTK = TK/q = 1,5q^2 - 22,5q + 120` en `GTK'(q) = 3q - 22,5 = 0` als `q = 7,5`.
      Dus bij een afzet van 7500 stuks.
5. 1. Nulpunten: `f(x)=0` geeft `x=-1/2 vv x=+-2`, dus `(-1/2,0)`, `(-2,0)` en `(2,0)`.
      Extremen: `f'(x) = 6x^2 + 2x - 8 = 0` geeft `x=-1 1/3 vv x=1`; max.`f(-1 1/3) = 3 19/27` en min.`f(1)=-9`.
   2. `f(x) = g(x)` geeft `x=0 vv x=+-2`.
      Oplossing: `-2 < x < 0 vv x > 2`.
6. 1. Lengte = `l`, breedte = `2h` en hoogte = `h`.
      `l + 8h = 120` en `I = l * 2h^2` geeft `I = 2h^2(120 - 8h) = 240h^2 - 16h^3`.
      `I'(x) = 480h - 48h^2 = 0` geeft `h=0 vv h=10`, alleen `h=10` levert een maximum op.
      `h=10` betekent `b=20` en `l=40`, dus `I=8000` cm³.
   2. Zelfde procedure als bij a, maar nu met `l + 8h = p` geeft: `h = 1/12 p`, `b = 1/6 p` en `l = 1/3 p`. Inderdaad is dan `b=2h` en `l=4h`.
7. 1. Zie website. Maak zelf een tabel voor de gegeven functie `TK` op je grafische rekenmachine.
   2. Bereken zowel `MK(4,5) ~~ TK'(4,5)` als `MK(4,5) = TK(4,501) - TK(4,5)` en laat zien dat beide ongeveer hetzelfde zijn.
   3. `TK` stijgt afnemend tot het buigpunt.
      Dat buigpunt zit bij `TK''(q) = 1,5q - 6 = 0`, dus bij `q = 6`. Dat is tot 6000 kg/mnd.
   4. `TW = 18q - (0,25q^3 - 3q^2 + 18q + 30) = -0,25q^3 + 3q^2 - 30`
   5. `TW = 0` geeft met de GR: `q ~~ 3,833 vv q ~~ 11,010`. Er wordt winst gemaakt bij een verkoop vanaf 3833 kg t/m 11010 kg/mnd.
   6. De winst is maximaal als `TW'(q) = MW(q) = -0,75q^2 + 6q = 0`.
      Dit geeft `q=0 vv q = 8` en er is sprake van maximale winst bij `q = 8`, dus bij een verkoop van 8000 kg/mnd. Die maximale winst bedraagt € 34000,00.
   7. Nu is `TW = (58,5 - 3q)q - (0,25q^3 - 3q^2 + 18q + 30) = -0,25q^3 + 40,5q - 30`.
      Je vindt nu een maximum als `TW'(q) = -0,75q^2 + 40,5 = 0`.
      Het maximum zit bij `q = sqrt(54) ~~ 7,348`. Er is nu maximale winst bij een productie van 7348 kg/mnd van ongeveer € 168409,00.
8. 
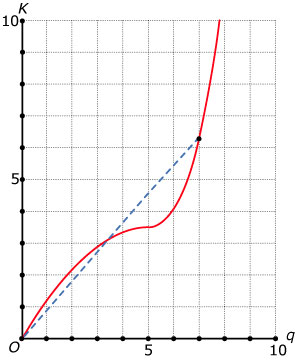
   1. Als `0 <= q < 5` is `(text(d)K)/(text(d)q) = -0,2q + 1,2 > 0`.
      Als `q >= 5` is `(text(d)K)/(text(d)q) = 0,3q^2 - 2,2q + 3,7 > 0` (dalparabool met nulpunten bij `q ~~ 2,6` en `q ~~ 4,7`).
   2. Als `0 <= q < 5` is `K'(q) = -0,2q + 1,2`. De laagste waarde is `K'(5) = 0,2`.
      Als `q >= 5` is `K'(q) = 0,3q^2 - 2,2q + 3,7`. De laagste waarde is `K'(5) = 0,2`.
   3. Bij een productie van 7000 stuks bedragen de gemiddelde kosten `(K(7))/7 = 0,9` euro.
      De lijn door `O` met dit hellingsgetal snijdt de grafiek bij `q=3`.
      Bij een productie van 3000 stuks bedragen de gemiddelde kosten inderdaad ook `(K(3))/3 = 0,9` euro.
9. 1. `A(2) = 30100`, dus de totale dagopbrengst is € 60200,00.
   2. `TO = A*T = 400T^3 - 9150T^2 + 46800T` moet maximaal zijn.
      `TO'(T) = 1200T^2 - 18300T + 46800 = 0` oplossen. De maximale opbrengst zit bij `T = 3,25`.
   3. `A(2,4) = 27144` en `A(2,52) ~~ 26282`. Er is dus een afname van ongeveer 3,18%.
   4. `T_(text(nieuw)) = 1,06 * T` en `A_(text(nieuw)) = 0,972 * A`.
      De nieuwe dagopbrengst wordt dan `T_(text(nieuw)) * A_(text(nieuw)) = 1,06 * 0,972 * A * T ~~ 1,03 * A * T`.
      De nieuwe dagopbrengst is dus ongeveer 3% meer.
10. 1. als `v = 17` dan `h = –0,0185a^2 + 0,27a + 2,50`.
       `h'(a) = –0,037a + 0,27 = 0` geeft `a ~~ 7,3`.
       Daarbij hoort een maximale hoogte van `h ~~ 3,5` m.
    2. 150 km/u komt overeen met 41,67 m/s.
       Volgens de grafiek hoort daar een hoek bij van ongeveer –5°.
    3. Bij de netsituatie: als `a = 12` dan `h = 1`.
       Dit geeft: `-(5,16)/(v^2) * 12^2 + 0,18 * 12 + 2,50 = 1` en dus `(743,04)/(v^2) = 3,66` en `v ~~ 14,25`. Conclusie: `v <= 14,2` (m/s) of `v < 14,3` (m/s).
    4. 7 meter voorbij het net betekent `a = 19` en de grond raken betekent `h = 0`.