
Totaalbeeld
Samenvatten
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Samenvatten
Je hebt nu het onderwerp Vectoren en goniometrie doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
- vector, lengte en richtingshoek componenten van een vector
- sinus, cosinus, tangens ook van hoeken groter dan 90°
- de sinusregel
- de cosinusregel
Activiteitenlijst:
- componenten van een vector bepalen door meting/berekening positieve/negatieve componenten onderscheiden
- componenten van vectoren berekenen m.b.v. sin en cos sin, cos en tan van hoeken (ook) boven 90° bepalen
- de sinusregel gebruiken in (niet-)rechthoekige driehoeken
- de cosinusregel gebruiken in (niet-)rechthoekige driehoeken
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Achtergronden
Testen
Opgaven
- Gegeven zijn deze vectoren door hun lengte `v` en hun richtingshoek `alpha`. Bereken de `x`-component en de `y`-component. Geef waar nodig benaderingen in twee decimalen nauwkeurig.
- `v = 20` en `alpha = 45^(text(o))`
- `v = 20` en `alpha = 115^(text(o))`
- `v = 20` en `alpha = 300^(text(o))`
- `v = 20` en `alpha = 270^(text(o))`
- Bereken alle overige zijden en hoeken van `Delta ABC` als gegeven is (geef waar nodig benaderingen in twee decimalen nauwkeurig):
-
`a = 5`, `b = 6` en `c = 4`
-
`a = 5`, `b = 6` en `gamma = 120^(text(o)`
-
`a = 5`, `b = 6` en `beta = 120^(text(o)`
-
`c = 12`, `alpha = 50^(text(o)` en `beta = 60^(text(o))`
-
`a = 12`, `b = 6` en `alpha = 90^(text(o)`
-
`a = b = 10` en `gamma = 81^(text(o)`
De breedte van een rivier
De breedte van een rivier bepaal je vanuit een duidelijk herkenbaar punt `P` op de tegenover liggende oever. Langs de oever waarop je zelf staat zet je een lijnstuk `AB` van bijvoorbeeld 10 m uit.
Vervolgens meet je de hoeken van `AP` met `AB` en van `BP` met `AB`. Bereken de breedte van de rivier als `/_BAP = 65^(text(o))` en `/_ABP = 54^(text(o))`.
abc-tjes
Gegeven is een driehoek waarvan de lengtes van de zijden `a`, `b` en `c` zijn. Bereken in de volgende gevallen de grootte van de hoek tegenover de zijde met lengte `a`.
-
`a^2 = b^2 + c^2`
-
`a^2 = b^2 + c^2 - bc`
-
`a^2 = b^2 + c^2 + 0,5bc`
-
Tussen drie palen die loodrecht op de grond staan is heel strak een driehoekig zeil gespannen. Paal 1 staat 5 m van paal 2, paal 2 staat 4 m van paal 3 en paal 3 staat 3 m van paal 1.
Het zeil is op 2 m boven de grond aan paal 1, op 2,5 m boven de grond aan paal 2 en op 3,50 m boven de grond aan paal 3 bevestigd.
Bereken de oppervlakte van dit zeil.
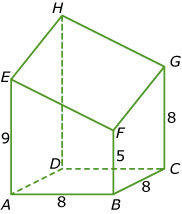 Je ziet hier een afgeknotte driezijdige balk `ABCD.EFGH`.
De afmetingen in cm staan in de figuur.
Je ziet hier een afgeknotte driezijdige balk `ABCD.EFGH`.
De afmetingen in cm staan in de figuur.
-
Hoe lang is `DH`? Licht het antwoord toe.
-
Bereken de grootte van `/_EHG` in graden nauwkeurig.
-
Bereken de oppervlakte van het bovenvlak `EFGH` in mm2 nauwkeurig.
Toepassen
De afstand Aarde Maan
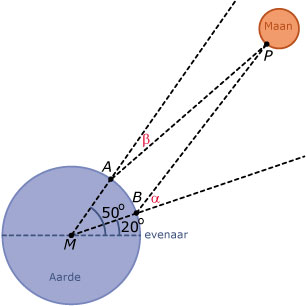 De afstand van het middelpunt `M` van de Aarde tot een punt `P` op de Maan kun je berekenen door op dezelfde lengtegraad op twee verschillende punten `A` en `B` een kijker op punt `P` te richten. Neem aan dat de Aarde een zuivere bol is met een omtrek van 40.000 km en neem ook aan dat de Maan precies recht boven de lengtegraad staat waar `A` en `B` op liggen, dus `M, A, B` en `P` liggen in één vlak. Je meet nu de hoeken die de kijker met `MA` en met `MB` maakt (dus met lijnen loodrecht op het aardoppervlak). Stel dat `A` op 50° N.B. ligt en `B` op 20° N.B.
De afstand van het middelpunt `M` van de Aarde tot een punt `P` op de Maan kun je berekenen door op dezelfde lengtegraad op twee verschillende punten `A` en `B` een kijker op punt `P` te richten. Neem aan dat de Aarde een zuivere bol is met een omtrek van 40.000 km en neem ook aan dat de Maan precies recht boven de lengtegraad staat waar `A` en `B` op liggen, dus `M, A, B` en `P` liggen in één vlak. Je meet nu de hoeken die de kijker met `MA` en met `MB` maakt (dus met lijnen loodrecht op het aardoppervlak). Stel dat `A` op 50° N.B. ligt en `B` op 20° N.B.
Beschrijf hoe je vanuit de gemeten hoeken de afstand `MP` berekent.
De clootcrans van Stevin
In een tijd dat krachten nog niet als vectoren werden ontbonden bedacht Simon Stevin wat de kracht moet zijn die een massa uitoefent op een helling. Hij deed dat niet door een experiment, maar door een simpele redenering.
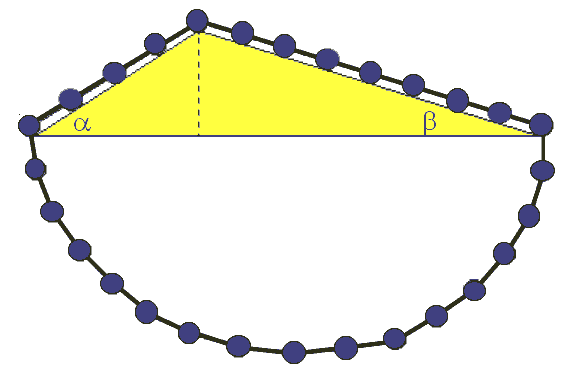
Hang een ketting van kralen over een punt dat twee hellingen verbindt. Welke kracht oefent de ketting uit op het punt, vanaf links en vanaf rechts?
Het vrij hangende gedeelte trekt aan beide kanten even hard.
De ketting beweegt niet, dus het gewicht van de ketting links is evenredig met de lengte van de helling links. De kracht die dat gewicht dan effectief uitoefent moet gelijk zijn aan de kracht die het rechterstuk uitoefent. Dus moet die kracht evenredig zijn met de lengte van de andere zijde. Dus verhouden de krachten zich omgekeerd met de lengtes van de hellingen. Je kunt dit ook controleren door de krachten te ontbinden in vectoren. En dan de sinuregel toe te passen. Laat zien hoe dat gaat.
(Zie ook: Clootcransbewijs in Wikipedia)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Samenvatten![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Totaalbeeld > Achtergronden Je ziet hier een afgeknotte driezijdige balk `ABCD.EFGH`.
De afmetingen in cm staan in de figuur.
Je ziet hier een afgeknotte driezijdige balk `ABCD.EFGH`.
De afmetingen in cm staan in de figuur.
 De afstand van het middelpunt `M` van de Aarde tot een punt `P` op de Maan kun je berekenen door op dezelfde lengtegraad op twee verschillende punten `A` en `B` een kijker op punt `P` te richten. Neem aan dat de Aarde een zuivere bol is met een omtrek van 40.000 km en neem ook aan dat de Maan precies recht boven de lengtegraad staat waar `A` en `B` op liggen, dus `M, A, B` en `P` liggen in één vlak. Je meet nu de hoeken die de kijker met `MA` en met `MB` maakt (dus met lijnen loodrecht op het aardoppervlak). Stel dat `A` op 50° N.B. ligt en `B` op 20° N.B.
De afstand van het middelpunt `M` van de Aarde tot een punt `P` op de Maan kun je berekenen door op dezelfde lengtegraad op twee verschillende punten `A` en `B` een kijker op punt `P` te richten. Neem aan dat de Aarde een zuivere bol is met een omtrek van 40.000 km en neem ook aan dat de Maan precies recht boven de lengtegraad staat waar `A` en `B` op liggen, dus `M, A, B` en `P` liggen in één vlak. Je meet nu de hoeken die de kijker met `MA` en met `MB` maakt (dus met lijnen loodrecht op het aardoppervlak). Stel dat `A` op 50° N.B. ligt en `B` op 20° N.B.