3D toepassingen

Antwoorden bij de opgaven

    1. Omdat je dan in twee dimensies kunt werken en je daarvoor over voldoende rekentechniek beschikt.
    2. `|QT|^2 = |BT|^2 - |BQ|^2 = 20^2 - 10^2 = 300`
    3. Beide driehoeken hebbe gelijke hoeken: een gemeenschappelijke `/_T` en een rechte hoek (en dan zijn de andere hoeken ook aan elkaar gelijk).
    4. `|TB|^2 = |TQ|^2 - |SQ|^2 = 300 - 100 = 200` dus `|TS| = sqrt(200)` en `|TM| = sqrt(200) - r`
    5. `(sqrt(200) - r)/(r) = (sqrt(300))/(10)` geeft `r = (10 sqrt(2))/(1 = sqrt(3))~~ 5,18`
  2. In `Delta QST` geldt `cos(/_Q) = 1/(sqrt(3))`.
    En in `Delta MRT` is `cos(/_M) = 1/(sqrt(3)) = (r)/(sqrt(200) - r)` en dan vind je weer `r ~~ 5,18`.
    1. Omdat je daarin die afstand goed kunt tekenen.
    2. -
    3. -
    4. Met gelijkvormigheid: `(sqrt(200))/(d + r) = 20/(sqrt(200) - r)` en met de al bekende `r` vind je `d ~~ 1,16`.
    1. `|TS| = sqrt(6^2 - 3,6^2) = 4,8`
    2. -
    3. De breedte is 3,45 m.
    4. De lengte is `4 19/24 ~~ 4,79` m.
    1. -
    2. De dakoppervlakte is twee keer de oppervlakte van `Delta BCT` plus die van `Delta CDT` en dat is `60 + 39,93... ~~ 100` m2.
    1. `|EH| = |HG| = 5` en `|EG| = sqrt(32)`
    2. `32 = 5^2 + 5^2 - 2 * 5 * 5 * cos(/_EHG)` geeft `/_EHG ~~ 69^(text(o))`
    3. `|HA| = sqrt(80)`, `|AB| = 5` en `|BH| = sqrt(96)`.
      De cos-regel geeft dan `80 = 5^2 + 96 - 2 * 5 * sqrt(96) * cos(/_ABH)` en dus `/_ABH ~~ 65^(text(o))`.
    1. -
    2. Het is de hoogtelijn vanuit `G` op `EH` in `Delta EHG`.
    3. De lengte van die hoogtelijn is `5 sin(/_EHG) ~~ 5 sin(69^text(o)) ~~ 4,7`.
    1. -
    2. -
    3. 561 cm.
    1. In `Delta FPB` geldt: `cos(/_F) = 1/6`.
      Met de cos-regel in `Delta BFG` krijg je dan: `|BG|^2 = 4^2 + 6^2 - 2 * 4 * 6 * cos(/_F) = 46`, dus `|BG| = sqrt(46)`
    2. In trapezium `ABGH` is `cos(/_B) = (1,5)/(sqrt(46)`.
      Met de cos-regel in `Delta ABG` krijg je dan: `|AG|^2 = 4^2 + 46 - 2 * 4 * sqrt(46) * cos(/_B) = 50`, dus `|AG| = sqrt(50)`
    1. `cos(/_BAE) = (1,5)/6` dus `/_BAE ~~ 76^(text(o))`.
    2. Pas de cos-regel toe in `Delta ACG`: `(sqrt(17))^2 = 6^2 + (sqrt(50))^2 - 2 * 6 * sqrt(50) * cos(/_AGC)` geeft `/_AGC ~~ 34^(text(o))`.
  11. De doorsnede op hoogte `x` heeft een lengte van `l = 4 - (3x)/(sqrt(31,5))` en `b = 1 + (3x)/(sqrt(31,5))`.
    De omtrek is daarom altijd 10 m.
    1. Punt `A` zit dan op `sqrt(100^2 - 30^2) = sqrt(9100)` van de muur.
      `|AC| = sqrt(120^2 + (sqrt(9100))^2) = sqrt(23500)`.
    2. De draaihoek is `/_ABC` als `A` op zijn laagste stand zit. Die hoek kun je rechtstreeks met de cos-regel in `Delta BAC` berekenen. Of je berekent het supplement van die hoek in de rechthoekige driehoek die daar onder zit. Je vindt `/_ABC ~~ 107,4^(text(o))`. De baanlengte is dan ongeveer `(107,4)/(360) * 2pi * 100 ~~ 188` cm.
    3. `sqrt(100^2 - 20^2) = sqrt(9600)` cm.
    4. `a = 90 * sin(beta)`.
    5. Ala `a = 45`, is `beta = 30^(text(o))` en daarmee vind je voor de gevraagde afstand 50 cm.
    1. De straal is `sqrt(16^2 - 5^2) = sqrt(231) ~~ 15,2` cm.
    2. `sin(1/2 /_FEL) = 5/16` dus `/_FEL ~~ 36,4^(text(o))` dus 10 dozen.
    3. Het gaat om de lengte van het lijnstuk van het midden `M` van `DE` naar het midden `N` van `CK`.
      Met gelijkvormigheid toon je aan dat `|DN| = 13/16 sqrt(231)` en omdat `|DN| = 7` is `|MN| = sqrt(13/16 sqrt(231))^2 + 7^2)`. En dat in minder dan de straal van de kaas. Dus hij past niet... (Best raar voor een opgave uit een oud havo wiskunde B examen, waar overigens deze vraag niet werd gesteld.)
    4. Symmetrisch trapezium met `|BH| = 10`, `|CK| = 13/16 * 10` en `|HK| = |BC| = sqrt(18)`.
      De hoeken zijn `/_B = /_H ~~ 77,2^(text(o))` en `/_C = /_K ~~ 102,8^(text(o))`.
    1. `sqrt(40^2 + 40^2) = sqrt(3200) = 40sqrt(2) ~~ 57` cm.
    2. De afstand van het draaipunt naar de uiterste punten van de halve cirkel is `sqrt(20^2 + 80^2) = sqrt(6800)` cm. Omdat het draaipunt 40 cm van de muur zit, is de gevraagde afstand `2 * sqrt(6800 - 40^2) = 2 * sqrt(5200) ~~ 144` cm.
    3. Omdat het glazen oppervlak een kwart cirkel is, staat in de twee uiterste punten de (kwart) cirkelboog loodrecht op de rechte rand van het tafelblad. Die rechte rand maakt een hoek van ongeveer 29,0° (goniometrie) met de muur, de ronde rand maakt dus een hoek van ongeveer 119,0° met de muur. Nu geef je normaal gesproken een scherpe hoek, dus het juiste antwoord is 61,0°.
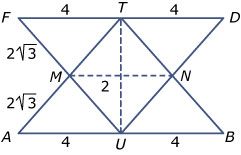
    1. `TU` is lichaamsdiagonaal van een regelmatig achtvlak (`T.PQRS.U`) waarvan alle ribben 4 zijn. De lengte is `4 sqrt(2)`. Je kunt ook werken in deze dwarsdoorsnede die vooral ook bij de volgende twee ondredelen handig is.
    2. Bekijk de dwarsdoorsnede. Omdat je nu weet dat `|AF| = |TU| = 4sqrt(2)` kun je (bijvoorbeeld) met de cos-regel in `Delta AMF` de gevraagde `/_AMF` uitrekenen. Maar vanwege de symmetrie kan het ook heel gewoon met sin, cos of tan. Uiteindelijk vind je `/_AMF ~~ 109,47^(text(o))`.
    3. De straal van die bol is `r = |SF|` als `S` het snijpunt van `TU` en `MN` is. `r = sqrt(24)`.