De cosinusregel

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De cosinusregel > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De cosinusregel > Uitleg

Lees eerst de Uitleg goed door.

  1. Bekijk in de Uitleg wat de cosinusregel is.
    Leid zelf de cosinusregel af.

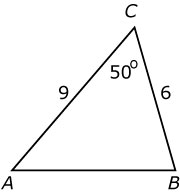  2. Hier zie je een driehoek ABC met twee zijden en de ingesloten hoek gegeven.
    1. Hoe ziet de cosinusregel bij de gegeven hoek er uit?
    2. Bereken de derde zijde van deze driehoek.

  3. Wanneer moet je in een driehoek werken met de cosinusregel omdat de sinusregel geen oplossing biedt?

  4. Gebruik de cosinusregel om het probleem bij Verkennen op te lossen.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De cosinusregel > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

  1. In Voorbeeld 1 zie je de constructie van `Delta ABC` als gegeven is `/_A = 20^(text(o))`, `|AB| = 6` cm en `|AC| = 4` cm.
    1. Construeer zelf deze driehoek.
    2. Controleer dat inderdaad `|BC| ~~ 2,63`.

  2. Bekijk in Voorbeeld 2 de constructie van `Delta ABC` met `|AB| = 6` cm, `|AC| = 4` cm en `|BC| = 3` cm.
    1. Voer zelf de berekening van `/_A` uit.
    2. Bereken nu ook `/_B`. Heb je opnieuw de cosinusregel gebruikt? En zo ja, kon dit ook met de sinusregel?


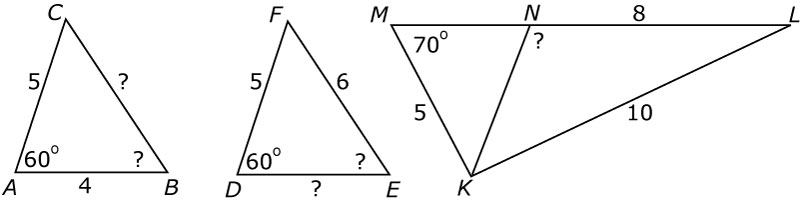
  3. Bereken de onbekende zijden en de onbekende hoeken in de volgende figuren.




  4. Laat zien dat de stelling van Pythagoras een speciaal geval is van de cosinusregel.

  5. Stel je voor dat op 60 km van een eiland je schip in dichte mist vergaat.
    Je kunt jezelf drijvend houden op een vlot, maar alle instrumenten zijn verloren. Natuurlijk probeer je dan rechtstreeks naar dat eiland te peddelen. Je legt ongeveer 2,5 km per uur af. Zonder dat je dat weet staat er een stroming die er voor zorgt dat je 30° uit de koers raakt. Na 20 uur zou je nog 10 km van het eiland verwijderd moeten zijn, als je er inderdaad recht naar toe gepeddeld was.
    Hoe ver ben je er in werkelijkheid vanaf?

  6. Van een `Delta ABC` is gegeven dat `|AB| = 10`, `|AC| = 6` en `/_C = 60^(text(o))`.
    Gebruik de cosinusregel om de lengte van zijde `BC` uit te rekenen.

Verwerken

  1. Elke `Delta ABC` heeft zes afmetingen, te weten: Hieronder zijn steeds drie maten van `Delta ABC` gegeven. Bereken de andere maten (exact waar mogelijk).
    1. `a = 8`, `b = 5` en `gamma = 65^(text(o)`
    2. `a = 8`, `b = 5` en `alpha = 65^(text(o)`
    3. `c = 150`, `gamma = 120^(text(o)` en `beta = 45^(text(o))`
    4. `a = 6`, `b = 10` en `c = 8`
    5. `a = b = 15` en `gamma = 20^(text(o)`

  2. Teken het trapezium `ABCD` met `|AB| = 12`, `|AC| = 10`, `|DC| = 4` en `/_B = 45^(text(o))`.
    Omdat de vierhoek `ABCD` een trapezium is, is `AB` evenwijdig met `CD`.
    Bereken de lengte van `AD`.

  3. Laat met een berekening zien dat een driehoek `ABC` met `|AB| = 12`, `|AC| = 8` en `/_B = 45^(text(o))` onmogelijk is.

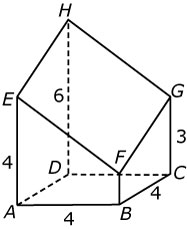  4. Je ziet hier een afgeknotte balk `ABCD.EFGH`.
    De afmetingen staan in de figuur.
    Bereken de grootte van `/_EHG` met behulp van de cosinusregel in `Delta EHG`.

  5. Van een viervlak `ABC.D` zijn de ribben achtereenvolgens `|AB| = 4` cm, `|BC| = 5` cm, `|AC| = 6` cm, `|AD| = 7` cm, `|BD| = 8` cm en `|CD| = 9` cm. Punt `P` is het midden van `AC` en punt `Q` is het midden van `BD`.
    Bereken de lengte van `PQ`.

Testen

  1. Van een driehoek `ABC` is gegeven `|AC| = b = 12`, `|AB| = c = 15` en `/_A = alpha = 55^(text(o)`. Bereken de lengte van `BC` in twee decimalen nauwkeurig.

  2. Van een driehoek zijn de zijden respectievelijk 8, 5 en 4 cm. Bereken de grootte van de hoeken.