De sinusregel

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De sinusregel > Inleiding

Probeer de vraag bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De sinusregel > Uitleg

Lees eerst de Uitleg goed door.

1. Bekijk in de Uitleg wat de sinusregel is.
   Gebruik de sinusregel om het probleem bij Verkennen op te lossen. Hulplijnen zijn nu overbodig.
   


2. Teken `Delta ABC` met `|AB| = 4` cm, `/_A = 30^(text(o))` en `/_C = 70^(text(o))`.
   Bereken de lengte van `BC` in twee decimalen nauwkeurig.
   


3. Teken `Delta DEF` met `|DE| = 4` cm, `/_D = 30^(text(o))` en `/_E = 70^(text(o))`.
   Bereken de lengte van `DF` in twee decimalen nauwkeurig.
   


4. Je kunt ook afleiden: `a/(sin(alpha)) = c/(sin(gamma))`. Laat dat zien.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > De sinusregel > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

5. In Voorbeeld 1 zie je de constructie van `Delta ABC` als gegeven is `/_A = 20^(text(o))`, `/_B = 50^(text(o))` en `|AB| = 6` cm.
   1. Construeer zelf deze driehoek.
   2. Waarom is het voor het berekenen van de lengte van `AC` nodig om `/_C` te berekenen?
   3. Controleer dat inderdaad `|AC| ~~ 4,89`.


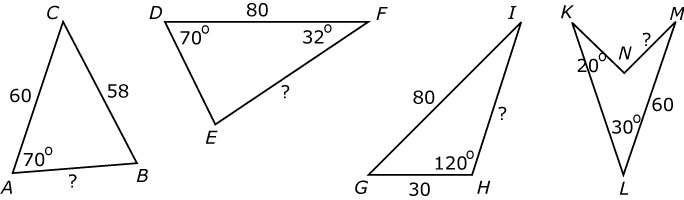
6. Bereken in de volgende figuren de zijde waar het vraagteken bij staat. Vierhoek `KLMN` is een symmetrische pijlpuntvlieger.
   
   
   
   


7. Je kunt de sinusregel op meerdere manieren schrijven.
   Bijvoorbeeld ook zo: `(sin(alpha))/a = (sin(beta))/b = (sin(gamma))/c`.
   Bedenk nog twee manieren waarop je de sinusregel kunt schrijven.
   


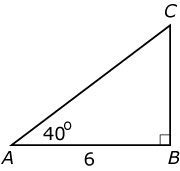8. In deze rechthoekige driehoek kun de lengte van `AC` berekenen met behulp van de sinusregel.
   1. Laat zien hoe dat gaat.
   2. Bereken `|AC|` ook zonder de sinusregel te gebruiken.


9. Bekijk Voorbeeld 2.
   Teken `Delta KLM` met `/_K = 30^(text(o))`, `|KL| = 5` cm en `|LM| = 4` cm.
   Construeer de twee mogelijke driehoeken en bereken telkens de lengte van `KM`.
   
   


10. Van een `Delta ABC` is `|AB| = 20`, `|BC| = 15` en `/_A = 60^(text(o))`.
    1. Toon aan dat `sin(/_C) = 2/3`.
    2. Welke hoeken voldoen aan `sin(/_C) = 2/3`?
    3. Je berekent hoeken uit een driehoek. Welke hoek voldoet?
    4. Bereken nu de lengte van `AC`.

Verwerken

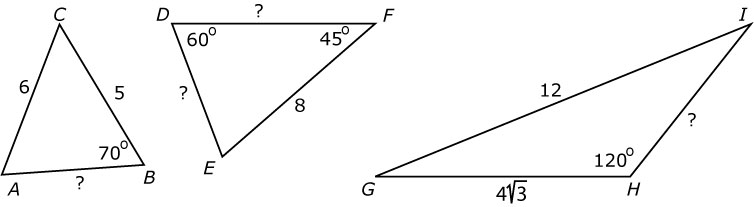
11. Bereken (exact waar mogelijk) de zijde waar het vraagteken bij staat.
    
    
    
    


12. Je wilt de lengte bepalen van lijnstuk `AB`, maar tussen de punten `A` en `B` ligt een meertje. Je gaat nu als volgt te werk:
    • Je loopt 200 m in een richting die een hoek van 60° maakt met `AB`. Zo houd je droge voeten.
    • Je bent in een punt dat je `P` noemt en meet de hoek tussen `AP` en `PB`: 80°.
    • Vervolgens bereken je de lengte van `AB`.
    Laat met een tekening zien hoe dit in zijn werk gaat en bereken de lengte van `AB`.
    



13. De hoogte van een toren

    Iemand wil de hoogte van een toren weten. Hij gaat een stuk van de toren vandaan staan en meet de hoek tussen de horizontale richting en de richting naar de spits van de toren. Deze hoek is 32°. Dan loopt hij 50 m van de toren vandaan en meet de hoek naar de top opnieuw; de hoek is nu 15°.
    1. Maak een tekening van deze situatie.
    2. Bereken de hoogte van de toren in m nauwkeurig. Ga er daarbij vanuit dat beide hoeken op 1,80 m boven de grond zijn gemeten.
       (Opmerking: Er is een oplossing van dit probleem waarbij je de sinusregel gebruikt, maar er is ook wel een oplossing te bedenken waarbij dit niet hoeft. Kun je beide oplossingen vinden?)
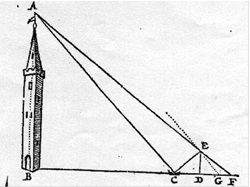
    3. De Nederlandse meetkundige Sybrandt Hansz. Cardinael (1578 – 1647) bedacht een zeer elegante manier om de hoogte van een toren te bepalen. Je hebt er zelfs geen hoeken voor nodig. Hier zie je hoe hij te werk ging. De toren is `AB` en er ligt een spiegel op de grond in `C`. Je zet bij `D` een verticale stok `DE` met lengte 6 zo, dat de top `A` van de toren in de spiegel gezien kan worden vanuit `E`. Vervolgens bepaal je de plaats van punt `F` zo, dat vanuit `F` de top `A` juist boven de stok `DE` in het verlengde van `FE` gezien kan worden. Als `|CD| = 8` en `|DF| = 9`, kun je de hoogte van de toren `AB` berekenen. Laat zien hoe.



14. Landmeetkunde: voorwaartse insnijding

    Om de positie van een bepaald punt `P` in kaart te brengen werkten landmeters vroeger met de sinusregel. Daartoe werden de afstanden tot `P` vanuit bekende punten berekend. Door omcirkelen vanuit die bekende punten kon `P` op de kaart worden aangegeven. Deze procedure heette "voorwaartse insnijding". Deze methode werkt alleen in de "lagere geodesie", de landmeetkunde waarbij het aardoppervlak als plat kan worden beschouwd.
    Stel dat `A` en `B` de bekende punten zijn, ze liggen 125,3 m uit elkaar.
    Je wilt de positie van `P` bepalen.
    Je meet de hoeken `BAP` en `ABP`: `/_BAP = 68,3^(text(o))` en `/_ABP = 77,4^(text(o))`.
    Bereken nu de lengtes van `AP` en `BP`.
    

Testen

15. Bereken (exact indien mogelijk) in de twee onderstaande figuren de lengte van het lijnstuk waar een vraagteken bij staat.
    
    
    
    


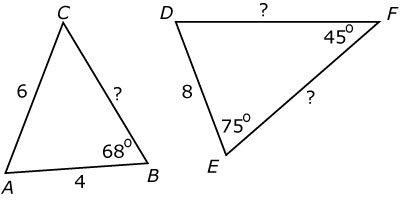
16. Teken `Delta ABC` met `/_B = 45^(text(o))`, `|BC| = 5` cm en `|AC| = 4` cm.
    Construeer de twee mogelijke driehoeken en bereken telkens de lengte van `AB` in twee decimalen nauwkeurig.