Sinus, cosinus en tangens

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Sin, cos, tan > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Sin, cos, tan > Uitleg

Lees eerst de Uitleg goed door.

  1. Bekijk de Uitleg. Laat met een tekening zien dat voor hoeken tussen 90° en 180° de cosinus van de hoek negatief en de sinus van de hoek positief is. En hoe zit het met de tangens van de hoek?

  2. Laat met behulp van een tekening zien, dat:
    1. `sin(100^(text(o))) = sin(80^(text(o)))`
    2. `cos(100^(text(o))) = -cos(80^(text(o)))`
    3. `sin(253^(text(o))) = -sin(73^(text(o)))`
    4. `cos(280^(text(o))) = cos(70^(text(o)))`

  3. Laat met behulp van een tekening zien, dat:
    1. `sin(alpha) = sin(180^(text(o)) - alpha)`
    2. `cos(alpha) = -cos(180^(text(o)) - alpha)`
    3. `sin(alpha) = -sin(-alpha)`
    4. `cos(alpha) = cos(-alpha)`

  4. Bereken met je rekenmachine in twee decimalen nauwkeurig de componenten van een verplaatsingsvector met lengte 1 bij een richtingshoek van:
    1. 40°
    2. 140°
    3. 240°
    4. 340°

  5. De verplaatsingsvectoren van de vorige opgave hebben nu allemaal een lengte van 500 km. Wat betekent dit voor alle Noordelijke en Oostelijke componenten?

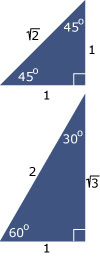
  6. Exacte waarden voor sin, cos en tan

    Van een paar hoeken kun je sinus, de cosinus en de tangens exact berekenen. Omdat die hoeken regelmatig voorkomen is het handig om die exacte waarden te weten. Bekijk daartoe deze twee bijzondere tekendriehoeken. De linker is een halve gelijkzijdige driehoek en de rechter is een geodriehoek.
    1. Bereken sinus, cosinus en tangens van 60° en van 30°.
    2. Bereken sinus, cosinus en tangens van 45°.
    3. Maak een tabel met de exacte waarden van sinus, cosinus en tangens van 0°, 30°, 45°, 60° en 90° (en leer hem uit je hoofd).

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Sin, cos, tan > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen. Zorg ervoor dat je de exacte waarden van de sinus, cosinus en tangens van 0°, 30°, 45°, 60° en 90° uit je hoofd kent!

Opgaven

  1. In Voorbeeld 1 zie je hoe je de exacte waarden van de sinus, de cosinus en de tangens van 120° kunt afleiden uit die van 60°. Bepaal nu zelf de exacte waarden van sin, cos en tan van 240° en 300°.

  2. Teken in een cartesisch assenstelsel een vector met lengte 1 en richtingshoek 45°.
    1. Bepaal de exacte waarden van `sin(135^(text(o)))`, `cos(135^(text(o)))` en `tan(135^(text(o)))`.
    2. Bepaal de exacte waarden van `sin(225^(text(o)))`, `cos(225^(text(o)))` en `tan(225^(text(o)))`.
    3. Bepaal de exacte waarden van `sin(315^(text(o)))`, `cos(315^(text(o)))` en `tan(315^(text(o)))`.

  3. Teken in een cartesisch assenstelsel een vector met lengte 1 en richtingshoek 30°.
    1. Bepaal de exacte waarden van `sin(150^(text(o)))`, `cos(150^(text(o)))` en `tan(150^(text(o)))`.
    2. Bepaal de exacte waarden van `sin(210^(text(o)))`, `cos(210^(text(o)))` en `tan(210^(text(o)))`.
    3. Bepaal de exacte waarden van `sin(330^(text(o)))`, `cos(330^(text(o)))` en `tan(330^(text(o)))`.

  4. Gebruik indien mogelijk de exacte waarden van sinus, cosinus en tangens van 0°, 30°, 45°, 60° en 90°.
    1. Bepaal alle hoeken tussen 0° en 360° die voldoen aan `cos(alpha) = 1/2`.
    2. Bepaal in graden nauwkeurig alle hoeken tussen 0° en 360° die voldoen aan `sin(beta) = -0,6`.
    3. Bepaal in graden nauwkeurig alle hoeken tussen 0° en 360° die voldoen aan `tan(gamma) = -0,6`.

  5. Bekijk Voorbeeld 2.
    Een schip vaart 80 km met een koers van 215° t.o.v. het Noorden. Dergelijke kompaskoersen worden altijd rechtsom gemeten! Hoeveel heeft het schip zich in Noordelijke of Zuidelijke richting verplaatst? En hoeveel in de Oostelijke of de Westelijke richting? (Geef je antwoorden in één decimaal nauwkeurig.)

  6. Neem eerst Voorbeeld 3 door.
    Teken `Delta KLM` met `/_K = 60^(text(o))`, `/_M = 45^(text(o))` en `|LM| = 4` cm.
    Bereken de exacte lengte van `KL` en `KM`.

  7. Teken `Delta PQR` met `/_P = 50^(text(o))`, `/_Q = 35^(text(o))` en `|PR| = 6` cm.
    Bereken de lengte van `PQ` en `QR`. Geef benaderingen in twee decimalen nauwkeurig.

Verwerken

  1. Bereken de `x`- en de `y`-componenten van de volgende vectoren. Geef waar mogelijk exacte uitkomsten, anders benaderingen in twee decimalen nauwkeurig.
    1. `|vec(v)| = 3` en `alpha = 135^(text(o))`
    2. `|vec(v)| = 5` en `alpha = 210^(text(o))`
    3. `|vec(v)| = 4` en `alpha = 320^(text(o))`
    4. `|vec(v)| = 2` en `alpha = 270^(text(o))`
    5. `|vec(v)| = 3` en `alpha = 115^(text(o))`
    6. `|vec(v)| = 1` en `alpha = 193^(text(o))`

  2. Bereken in graden nauwkeurig alle hoeken `alpha` met `0^(text(o)) <= alpha <= 360^(text(o))` waarvoor geldt:
    1. `cos(alpha) = 0,38`
    2. `sin(alpha) = 0,38`
    3. `cos(alpha) = -0,38`
    4. `sin(alpha) = -0,38`
    5. `2 cos(alpha) = 0,38`
    6. `tan(alpha) = 0,38`
    7. `cos(alpha) = 0`
    8. `cos(alpha) = 1`

  3. Teken `Delta ABC` met `/_A = 120^(text(o))`, `/_B = 45^(text(o))` en `|AC| = 5` cm.
    Bereken de exacte lengte van `AB` en `BC`.

  4. Lorrie (2)

    Twee personen trekken elk aan een touw een lorrie (een wagentje op rails) voort. Ze lopen beide op dezelfde afstand van het midden van de rails. De hoek tussen beide touwen is 40°. De grootte van elke kracht is 8 N (newton).
    1. Bereken de kracht die ze samen uitoefenen in de bewegingsrichting van de lorrie in één decimaal nauwkeurig.
    2. Doe hetzelfde voor de situatie waarin de ene persoon trekt met een kracht van 8 N onder een hoek van 20° ten opzichte van de rails en de ander trekt met een kracht van 6 N onder een hoek van 15° ten opzichte van de rails.
    3. In welke van beide situaties loopt de lorrie soepeler over de rails? Verklaar je antwoord.

  5. Mansardedak

    Je ziet hier een foto van een huis met een zogenaamd mansardedak. De breedte van het huis is 6 m en de breedte van elk dakdeel is 2,5 m. De onderste dakdelen maken een hellingshoek van 65° met een horizontaal vlak.
    1. Bereken de hoogte van het huis als de dakgoot op 3 m boven de begane grond zit.
    2. Bereken de hellingshoek van de bovenste dakdelen.

Testen

  1. Gegeven zijn de punten `P(0,8)` en `Q(12,3)`.
    1. Bereken `|vec(PQ)|` en de hoek die `vec(PQ)` met de positieve `x`-as maakt.
    2. `vec(OR)` is even lang als `vec(PQ)` maar heeft een richtingshoek van 120° met de positieve `x`-as. Bereken de exacte coördinaten van `R`.

  2. Bereken (exact indien mogelijk, anders in graden nauwkeurig) alle hoeken `alpha` met `0^(text(o)) <= alpha <= 360^(text(o))` waarvoor geldt:
    1. `sin(alpha) = -0,83`
    2. `cos(alpha) = -1/2 sqrt(3)`

  3. Teken `Delta ABC` met `/_A = 30^(text(o))`, `/_B = 135^(text(o))` en `|AC| = 10` cm.
    Bereken de exacte lengte van `AB` en `BC`.

  4. Noodlanding (2)

    Een piloot vertrekt met zijn sportvliegtuig van vliegveld T en vliegt 3 uur met een constante snelheid van 140 km/h in de koers 30° ten opzichte van het Noorden. Daarna verandert hij zijn koers in 170° en de snelheid in 120 km/h. Na 1,5 uur moet hij een noodlanding maken.
    Over de radio geeft hij aan de verkeersleiding van vliegveld T door waar hij is geland en dat hij ernstig gewond is geraakt. Onmiddellijk wordt een helikopter gestuurd. Bereken de verplaatsingsvector van de helikopter.