
Vectoren
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Uitleg
Lees eerst de Uitleg goed door.
-
Bekijk de Uitleg. Hier zie je vier keer een verplaatsingsvector met lengte 400 op schaal getekend.
Bepaal door meting bij elke situatie de lengtes van de Noordelijke component en de Oostelijke component. Geef met behulp van mintekens de richting aan.
a. 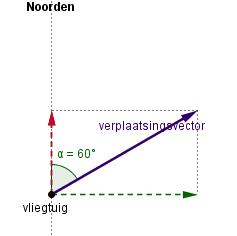 b.
b. 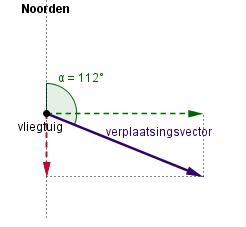
c. 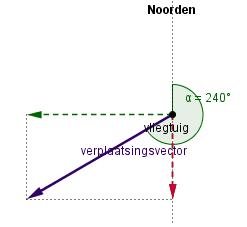 d.
d. 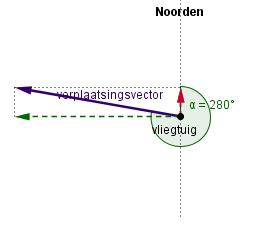
-
Van een verplaatsingsvector zijn de componenten gegeven. Teken die vector en bereken de lengte ervan. Bereken ook de grootte van de bijbehorende richtingshoek (met behulp van de tangens).
-
Noordelijke component: 200 km
Oostelijke component: 100 km
-
Noordelijke component: –300 km
Oostelijke component: 400 km
-
Noordelijke component: –200 km
Oostelijke component: 300 km
-
Noordelijke component: –200 km
Oostelijke component: –150 km
-
Noordelijke component: 0 km
Oostelijke component: –100 km
-
Noordelijke component: –200 km
Oostelijke component: 0 km
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
- In Voorbeeld 1 zie je hoe je kunt aantonen dat twee vectoren gelijk zijn.
Gegeven zijn in een cartesisch assenstelsel de punten `A(–2,1)`, `B(1,6)`, `C(28,12)` en `D(31,17)`.
Bereken `|vec(AB)|` en `|vec(CD)|` en de richtingshoeken van `vec(AB)` en `vec(CD)`. Laat daarmee zien dat beide vectoren gelijk zijn.
-
Bepaal lengte en richtingshoek van de volgende vectoren:
`vec(a) = ((12),(5))`, `vec(b) = ((-15),(7))`, `vec(c) = ((-5),(8))`, `vec(d) = ((0),(-5))`, `vec(e) = ((13),(0))` en `vec(f) = ((13),(-25))`.
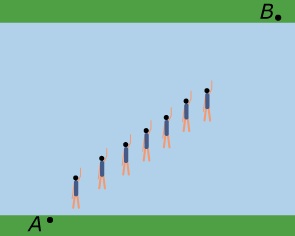 Een zwemmer probeert een rivier met een breedte van 60 m recht over te steken, maar heeft last van de stroming. Tot zijn verbazing komt hij niet recht tegenover zijn startpunt `A` op de andere oever aan, maar in een punt `B` dat verder stroomafwaarts ligt.
De snelheid waarmee de zwemmer AB aflegt bestaat zo uit twee componenten:
Een zwemmer probeert een rivier met een breedte van 60 m recht over te steken, maar heeft last van de stroming. Tot zijn verbazing komt hij niet recht tegenover zijn startpunt `A` op de andere oever aan, maar in een punt `B` dat verder stroomafwaarts ligt.
De snelheid waarmee de zwemmer AB aflegt bestaat zo uit twee componenten:
- een component loodrecht op de oever
- een component die gelijk is aan de stroomsnelheid van de rivier
De stroomsnelheid is 0,6 km/h en de zwemmer bereikt in 5 minuten de overkant van de rivier.
Hoeveel bedraagt de snelheid waarmee hij `AB` aflegt in km/h in tienden nauwkeurig?
-
Bekijk Voorbeeld 2 voor een toepassing van het werken met vectoren in de natuurkunde.
- Bekijk de beginsituatie in de applet. In feite is de 200 N de maximale wrijvingskracht. Hoe groot zal in dit geval de wrijvingskracht zijn?
- Bekijk nu met behulp van de applet bij welke hellingshoeken het gewicht blijft liggen.
- Leg uit waarom de hoek tussen de component loodrecht op het hellende vlak en de zwaartekracht altijd gelijk is aan de hellingshoek van het vlak.
- Voer nu zelf de berekening uit van de maximale hellingshoek waarbij het gewicht nog blijft liggen op het hellende vlak.
Practicum
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d >Meetkunde > Vectoren en goniometrie > Vectoren > GeoGebra I
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d >Meetkunde > Vectoren en goniometrie > Vectoren > GeoGebra I
Bekijk hoe je in het programma GeoGebra vectoren kunt maken. Let er op dat de vectornotatie in GeoGebra net zo is als die voor de coördinaten van punten!
Verwerken
-
Een vector `vect(v)` heeft een gegeven lengte en een gegeven richtingshoek `alpha` t.o.v. de positieve `x`-as. Teken deze vector en bepaal door meting de `x`-component en de `y`-component.
- `|vec(v)| = 3` en `alpha = 135^(text(o))`
- `|vec(v)| = 5` en `alpha = 210^(text(o))`
- `|vec(v)| = 4` en `alpha = 300^(text(o))`
- `|vec(v)| = 2` en `alpha = 270^(text(o))`
-
Gegeven is telkens een vector `vec(v)` door zijn `x`- en `y`-componenten. Bereken de lengte en de richtingshoek van deze vector.
- `vec(v) = ((-2),(4))`
- `vec(v) = ((-20),(-40))`
- `vec(v) = ((0),(-15))`
- `vec(v) = ((sqrt(15)),(-1))`
-
Gegeven is een vierhoek `ABCD` met hoekpunten `A(-23,61)`, `B(7,51)`, `C(-3,91)` en `D(-33,101)`. Punt `S` is het snijpunt van de diagonalen van `ABCD`.
- Bepaal de componenten van de vectoren `vec(AB)` en `vec(DC)`. Toon m.b.v. deze twee vectoren aan dat vierhoek `ABCD` een parallellogram is.
- Bepaal ook de componenten van de vectoren `vec(AS)`, `vec(SC)`, `vec(BS)` en `vec(SD)`. Toon m.b.v. deze vier vectoren aan dat vierhoek `ABCD` een parallellogram is.
 Iemand zwemt met een snelheid van 2 km/h schuin tegen de stroom van een rivier met een stroomsnelheid van 0,6 km/h in.
Daardoor steekt hij de rivier precies loodrecht op de oevers (en de stroomrichting) in de breedte over.
De rivier is 50 m breed. Hoe lang doet hij over de overtocht?
Iemand zwemt met een snelheid van 2 km/h schuin tegen de stroom van een rivier met een stroomsnelheid van 0,6 km/h in.
Daardoor steekt hij de rivier precies loodrecht op de oevers (en de stroomrichting) in de breedte over.
De rivier is 50 m breed. Hoe lang doet hij over de overtocht?
Lorrie (1)
Een lorrie is een karretje dat op rails loopt. Twee personen trekken de lorrie met dezelfde kracht van 8 N elk aan een touw, zie figuur.

-
Met welke kracht trekken beide personen samen aan het karretje in de richting van de rails?
-
Beantwoord dezelfde vraag als de éne persoon trekt met een kracht van 8 N en de andere met een kracht van 6 N. De hoeken blijven gelijk.
Testen
- Gegeven zijn de punten `P(0,12)` en `Q(8,2)`.
- Bereken `|vec(PQ)|` en de hoek die `vec(PQ)` met de positieve `x`-as maakt.
- `vec(OR)` is even lang als `vec(PQ)` maar heeft een richtingshoek van 120° met de positieve `x`-as. Bepaal door meting de coördinaten van `R`.
Noodlanding (1)
Een piloot vertrekt met zijn sportvliegtuig van vliegveld T en vliegt 3 uur met een constante snelheid van 140 km/h in de koers 30° ten opzichte van het Noorden.
Daarna verandert hij zijn koers in 170° en de snelheid in 120 km/h. Na 1,5 uur moet hij een noodlanding maken.
-
Maak van deze vlucht een tekening op schaal.
-
Over de radio geeft hij aan de verkeersleiding van vliegveld T door waar hij is geland en dat hij ernstig gewond is geraakt.
Onmiddellijk wordt een helikopter gestuurd. Bepaal de verplaatsingsvector van de helikopter.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Uitleg b.
b. 
 d.
d. 
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > Vectoren > Theorie Een zwemmer probeert een rivier met een breedte van 60 m recht over te steken, maar heeft last van de stroming. Tot zijn verbazing komt hij niet recht tegenover zijn startpunt `A` op de andere oever aan, maar in een punt `B` dat verder stroomafwaarts ligt.
De snelheid waarmee de zwemmer AB aflegt bestaat zo uit twee componenten:
Een zwemmer probeert een rivier met een breedte van 60 m recht over te steken, maar heeft last van de stroming. Tot zijn verbazing komt hij niet recht tegenover zijn startpunt `A` op de andere oever aan, maar in een punt `B` dat verder stroomafwaarts ligt.
De snelheid waarmee de zwemmer AB aflegt bestaat zo uit twee componenten:
![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d >Meetkunde > Vectoren en goniometrie > Vectoren > GeoGebra I
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d >Meetkunde > Vectoren en goniometrie > Vectoren > GeoGebra I Iemand zwemt met een snelheid van 2 km/h schuin tegen de stroom van een rivier met een stroomsnelheid van 0,6 km/h in.
Daardoor steekt hij de rivier precies loodrecht op de oevers (en de stroomrichting) in de breedte over.
De rivier is 50 m breed. Hoe lang doet hij over de overtocht?
Iemand zwemt met een snelheid van 2 km/h schuin tegen de stroom van een rivier met een stroomsnelheid van 0,6 km/h in.
Daardoor steekt hij de rivier precies loodrecht op de oevers (en de stroomrichting) in de breedte over.
De rivier is 50 m breed. Hoe lang doet hij over de overtocht?