Goniometrische functies

Inleiding

Muziek maak je door lucht in trilling te brengen. Dat doe je met een snaar, een holle buis, je stembanden, een trillend plaatje, e.d. Als je een snaar in trilling brengt hoor je behalve de grondtoon ook boventonen meeklinken. De frequenties van deze boventonen zijn een veelvoud van die van de grondtoon, maar ze klinken minder luid. Door de sinusoïden van de grondtoon en de boventonen op te tellen krijg je het trillingspatroon van de snaar.

Je leert nu:

• het begrip goniometrische functie;
• eigenschappen van dergelijke functies onderzoeken met de GR.

Je kunt al:

• werken met sinusoïden en vergelijkingen van de vorm sin(x) = a of sin(x) = a oplossen.

Verkennen

In de Westerse muziek worden zeven stamtonen onderscheiden, die samen een toonladder vormen. Deze zeven stamtonen worden aangeduid met A, B, C, D, E, F en G. De centrale A heeft een frequentie van 440 Hz (440 trillingen per seconde). Dit betekent dat in de lucht een trilling plaats vindt met die frequentie (is aantal trillingen per seconde). Voor de A geldt dan bijvoorbeeld
u₁(t) = a sin(440 · 2π · t).
De luidheid van deze grondtoon wordt bepaald door de amplitude a. Neem voor het gemak a = 1. De eerste boventoon van de A klinkt vaak minder luid, en dan geldt (bijvoorbeeld) u₂(t) = 0,8 sin(880 · 2π · t). Voor de tweede boventoon: u₃(t) = 1,2 sin(1320 · 2π · t). Tel je deze drie sinusfuncties op, dan krijg je een A met een bepaalde klankkleur.

> Breng eerst de grafiek van de grondtoon A maar eens in beeld met je grafische rekenmachine. Zorg dat je precies drie periodes in beeld krijgt.
> Zet de twee boventonen er bij en tel deze functies op.
> Is de resulterende snaartrilling een zuivere sinusoïde?

Uitleg

Je kent de functies f(x) = sin(x) en g(x) = cos(x) met x in radialen al. Omdat in de functies die trillingen beschrijven sinus en cosinus voorkomen, zijn het voorbeelden van goniometrische functies. De belangrijkste eigenschap is wel hun periodiciteit. De periode van deze functies is 2π. Hun amplitude is 1.

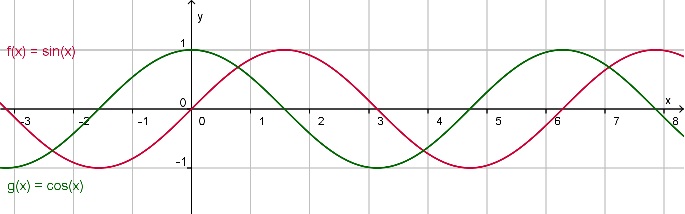
Bekijk je nu de functie u₂(t) = 0,8 sin(880 · 2π · t), dan worden alle waarden van sin(880 · 2π · t) met 0,8 vermenigvuldigd en dus is de amplitude 0,8.
Verder worden alle waarden van t met 880 · 2π vermenigvuldigd. Loopt t van 0 naar 1 dan worden er 880 periodes doorlopen. Elke herhaling duurt daarom 1/880 seconde.
Maar verder heeft de grafiek van u₂(t) = 0,8 sin(880 · 2π · t) dezelfde vorm als die van f(x) = sin(x). Maar wat als je sin(x) en/of cos(x) gaat gebruiken om ingewikkelder functievoorschriften te maken? Bekijk eerst maar eens een paar grafieken.

‡

Opgaven

1. Ga van elk van de volgende functies na of de grafiek op een sinusoïde lijkt of niet.
   1. `y_1 = 1 + 2 sin(0,5x – 1)`
   2. `y_2 = sin(x) + cos(x)`
   3. `y_3 = sin(x^2)`
   4. `y_4 = sin^2(x) = (sin(x))^2`
   5. `y_5 = sin(9x) – sin(11x)`


2. Waarom weet je bij `y_2` en `y_3` eigenlijk (nog) niet zeker of hun grafieken echt dezelfde vorm hebben als die van `y = sin(x)`?
   

Theorie

Onder goniometrische functies versta je functies waarin sin, cos (en tan) voorkomen.
De basisfuncties f(x) = sin(x) en
g(x) = cos(x) met x in radialen ken je al.
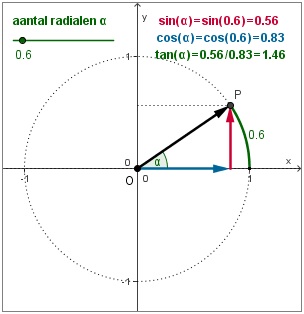
In deze eenheidscirkel zijn sinus en cosinus gedefinieerd als:

• sin(α) = y_P
• cos(α) = x_P

Hierin is α de lengte van boog AP waarin A = (1,0). De lengte van deze boog is ook een maat voor de grootte van hoek AOP die gemakshalve ook wel met α wordt aangeduid. Omdat de omtrek van één cirkel precies 2pi; is, herhalen de waarden van sin(α) en cos(α) zich elke periode van 2π. Ze kunnen alleen waarden aannemen vanaf –1 t/m 1.

Je kunt de waarden van sin(α) en cos(α) in grafieken uitzetten tegen α.
De grafieken van f(x) = sin(x) en g(x) = cos(x) hebben een periode van 2π en een amplitude van 1 en ze bewegen om een evenwichtsstand van 0.

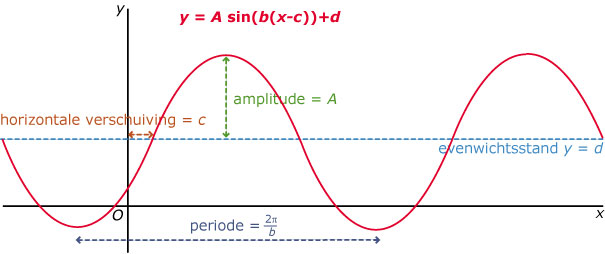
Sinusoïden zijn de grafieken van functies van de vorm:

f(x) = a sin(b(x – c)) + d

• periode: 2π/b
• amplitude: a
• evenwichtsstand: y = d
• horizontale verschuiving: c

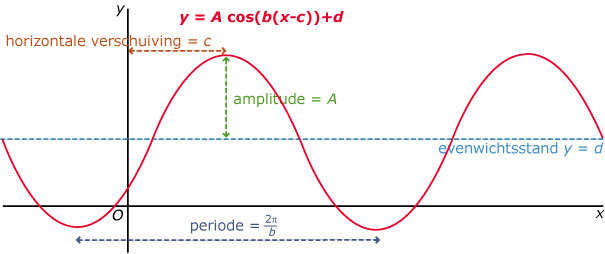
f(x) = a cos(b(x – c)) + d

• periode: 2π/b
• amplitude: a
• evenwichtsstand: y = d
• horizontale verschuiving: c

‡

Voorbeeld 1

Gegeven is de functie f met f(x) = 15 sin(4(x – 2)) + 150 op het interval [0,2π]. Breng de grafiek in beeld op je grafische rekenmachine en los op f(x) > 160.

Antwoord

Om de grafiek goed in beeld te krijgen, lees je eerst de amplitude en de evenwichtsstand uit de formule af: de amplitude is 15 en de evenwichtsstand is 150. De grafiek slingert dus om de lijn y = 150 en de y-waarden liggen in het interval [150 – 15, 150 + 15] = [135, 165].

Je stelt nu het venster van je rekenmachine zo in, dat 0 ≤ x ≤ 2π en (bijvoorbeeld) 130 ≤ y ≤170. Er komen precies 4 periodes in beeld. Dat kon je vooraf zien want de periode is 2π/4 = 0,5π.
Met je grafische rekenmachine kun je nu de ongelijkheid f(x) > 160 oplossen.

‡

Voorbeeld 2

Gegeven de functie f met voorschrift f(x) = 2 cos²(x) – 1.
(Met cos²(x) wordt (cos(x))² bedoeld.)
Onderzoek of deze goniometrische functie periodiek is en bepaal dan de bijbehorende periode.

Antwoord

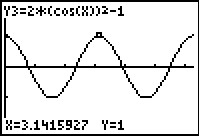
De standaard cosinusgrafiek heeft een periode van 2π. Het ligt dus voor de hand om de grafiek van f in beeld te brengen op bijvoorbeeld [0,2π]. Die grafiek lijkt op een zuivere sinusoïde met periode π, amplitude 1 en evenwichtsstand y = 0. Als je er een formule met cos bij wilt maken is de horizontale verschuiving 0.
Kortom: de grafiek lijkt op die van y = cos(2x).

Of dit echt het geval is, kun je (nog) niet aantonen. Wel kun je de nulpunten berekenen en kijken of die hetzelfde zijn als die van y = cos(2x).

f(x) = 0 als 2 cos²(x) – 1 = 0, dus als cos(x) = –$\sqrt{\mathrm{0,5}}$  V  cos(x) = $\sqrt{\mathrm{0,5}}$.
Dit levert dezelfde waarden op als cos(2x) = 0 oplossen.
Ga dat zelf na.

‡

Opgaven

3. Bekijk Voorbeeld 1. Los nu zelf op `[0,2pi]` op: `f(x) > 160`.
   


4. Gegeven is de functie `f` met `f(x) = 10 sin(0,1pi(x - 5)) + 15` op het interval `[0,50]`.
   1. Lees periode, amplitude, evenwichtsstand en de horizontale verschuiving t.o.v. de `y`-as uit het functievoorschrift af.
   2. Teken de grafiek met je grafische rekenmachine.
   3. Los op in twee decimalen nauwkeurig: `f(x) = 12`.


5. Bekijk Voorbeeld 2.
   1. Breng zelf de grafiek van `f` op je grafische rekenmachine in beeld en bepaal de twee opeenvolgende maxima.
   2. Welke periode kun je hieruit afleiden voor de sinusoïde die lijkt te ontstaan?
   3. Welke andere formule zou je bij deze sinusoïde kunnen opstellen?
   4. Waarom weet je nog niet helemaal zeker dat de grafiek van `f` ook echt een sinusoïde is?


6. Gegeven de functie `f` met `f(x) = 2 sin(x) cos(x)` op `[0,2pi]`.
   1. Maak de grafiek van `f` op je grafische rekenmachine.
   2. Lijkt de grafiek op een sinusoïde? Zo ja, welke formule past er dan bij die sinusoïde?
   3. Los op: `f(x) = 0,5`. Geef benaderingen in twee decimalen nauwkeurig.
   4. Gebruik nu de formule van de sinusoïde die je bij b hebt gemaakt en los exact op: `y = 0,5`. Komen deze antwoorden overeen met die bij c?


7. Bekijk de grafiek van de functie `f(x) = 2x sin(x)` op `[0,2pi]`.
   1. Waarom kan hier geen sprake zijn van een sinusoïde?
   2. Is dit een periodieke functie?
   3. Beschrijf de regelmaat van de grafiek van `f`.


8. Gegeven is de functie `f` met `f(x) = sin(sqrt(x))`.
   1. Maak de grafiek van `f` op `[0,1000]`.
   2. Los op: `f(x) = 1`.
   3. Hoe kun je aan de antwoorden bij b zien dat dit geen periodieke functie is?

Verwerken

9. Als je de sinusoïden `y_1 = 3 sin(x)` en `y_2 = 4 cos(x)` optelt, krijg je de grafiek van de functie `f(x) = 3 sin(x) + 4 cos(x)`. De grafiek van `f` is een sinusoïde.
   1. Geef de periode, de amplitude, de evenwichtsstand en de horizontale verschuiving ten opzichte van `y_1 = sin(x)`. Geef je antwoord in twee decimalen nauwkeurig.
   2. Stel een formule op voor deze sinusoïde.
   3. Bereken met behulp van je formule bij b de toppen en de nulpunten van de grafiek van `f`.
   4. Los op `[0,2pi]` op: `f(x) > 1`.


10. Bekijk de grafiek van de functie `g(x) = cos(x) - cos(2x)`.
    1. Deze grafiek is periodiek. Wat is de periode?
    2. Is de grafiek van `g` een sinusoïde?
    3. Bepaal met je grafische rekenmachine de nulpunten en de toppen van de functie `g`. Neem als domein `[0, 2pi]`.

Testen

11. Gegeven is de functie `f(x) = cos(x) - sin(x)`. De grafiek van `f` is een sinusoïde.
    1. Bereken of beredeneer de exacte nulpunten van `f`.
    2. Beredeneer de exacte extremen van `f`.
    3. Geef een formule voor deze sinusoïde.
    4. Los algebraïsch op: `f(x) >= 1`.