
Tonen en boventonen
The Soundry is een website gemaakt in het kader van Thinkquest. Hij gaat over geluid en is te vinden via de link http://library.thinkquest.org/19537/.
Wat is het doel van The Soundry?
|
The Soundry is an exciting, interactive, and educational web site about sound. Covering everything from the most basic concepts of what sound actually is to the specifics of how humans perceive it, The Soundry aims to promote enthusiasm and knowledge of sound. We hope you have fun exploring our site and come away with new understanding and insights about sound.
|
Op deze website vind je in het SoundLab de Harmonics Applet een eenvoudige on-line synthesizer. Je kunt er een toon op een tweetal instrumenten mee namaken en twee liedjes laten horen.
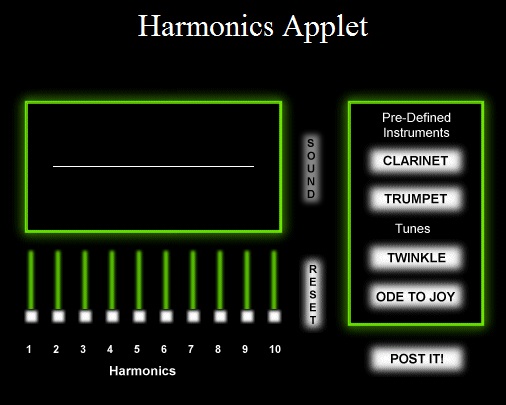
Als je de linker schuifregelaar 1 helemaal naar boven zet krijg je de A, een toon die overeen komt met eenzelfde trilling van de lucht die 440 keer per seconde plaats vindt. Dat heet de frequentie van de A, het aantal gelijke trillingen per seconde. De tijd waarin elke trilling plaats vindt heet de periode.
-
Stel dit basisgeluidsspoor in door de schuifregelaar 1 helemaal naar boven te zetten. (Het geluid is nogal saai, je kunt het aan/uit zetten naar believen).
- Herken je de grafiek die dit oplevert?
- Welke standaardfunctie hoort er bij die grafiek?
De grafiek van de A kun je beschrijven door de uitwijking u1 ten opzichte van de gegeven evenwichtslijn uit te zetten tegen de tijd t (in s).
Een bijpassende formule is dan: `u_1 = 2 sin(440 * 2pi * t)`.
- Leg uit waarom in dit geval het linker punt van de grafiek in de applet niet bij `t = 0` hoort.
- Licht toe hoe je aan deze formule kunt zien dat de A een frequentie heeft van 440 Herz (440 periodes per seconde).
- Breng de grafiek van `u_1` in beeld op je grafische rekenmachine. Breng de grafiek over drie periodes in beeld.
Je noemt zo’n grafiek een sinusoïde. Welke betekenis heeft het getal 2 in dit verband?
-
Zet nu de klarinet aan en bekijk zijn ingewikkelde geluidsspoor. De A op de klarinet bestaat kennelijk niet alleen uit de grondtoon, maar er klinken ook zogenaamde boventonen mee. Die boventonen (Engels: harmonics) hebben een frequentie die bijvoorbeeld 2 keer, of 3 keer, of 4 keer die van de grondtoon is, altijd een geheel aantal keer de frequentie van de grondtoon.
- Bekijk nu de eerste boventoon door schuifregelaar 2 helemaal omhoog te schuiven. Welke frequentie heeft die eerste boventoon van de A?
- Welke formule past er bij de uitwijking `u_2` van de eerste boventoon?
- De grafiek van `u(t) = u_1(t) + u_2(t)` kun je met de applet maken. Je ziet dan wat er gebeurt als ze gezamenlijk meeklinken. Doe dat zelf.
- Maak de grafiek van `u(t)` ook op je grafische rekenmachine. Is de grafiek van `u` af te leiden uit die van `y = sin(x)`?
- Welke formule hoort er bij `u(t)` als de eerste boventoon maar half zo duidelijk meeklinkt?
-
Er zijn nog veel meer boventonen. De golflengtes zijn steeds 1/3, 1/4, 1/5, etc., deel van de golflengte van de grondtoon. Schrijf nu passende formules op voor de uitwijking `u_3` van tweede boventoon, voor die van de derde en de vierde boventoon. Neem eerst maar even aan dat ze dezelfde stand van de schuifregelaar hebben.
-
Bij een toon gespeeld op een bepaald instrument klinken er meestal naast de grondtoon een aantal boventonen mee. Welke precies en hoe luid ze zijn wordt bepaald door het instrument, dit geeft de klankkleur van het instrument weer.
- Welke boventonen klinken er bij de klarinet mee?
- Stel een bijpassende formule voor `u(t)` op en maak de grafiek met je grafische rekenmachine. Vergelijk hem met die van de Harmonics Applet.
-
Maak ook een formule voor `u(t)` bij de trompet.
-
Maak met de Harmonics Applet zelf een geluidsspoor. Je kunt proberen andere instrumenten na te bootsen. Laat een medeleerling proberen een formule bij dit geluidsspoor te verzinnen. Waarom lijken de geluiden toch niet erg op echte instrumenten?

