Groeimodellen

Inleiding

Een belangrijk toepassingsgebied van exponentiële functies en dus ook van logaritmen zijn de verschillende groeimodellen die ermee kunnen worden beschreven. Behalve exponentiële groei, komen ook geremde groei en het logistische groeimodel voorbij. En ook zul je werken met twee soorten logaritmisch papier.

Je leert nu:

werken met enkellogaritmisch en dubbellogaritmisch grafiekenpapier;
groeimodellen opstellen en de eigenschappen ervan kennen.

Je kunt al:

werken met exponentiële functies, logaritmische functies en machtsfuncties;
differentiëren met de machtsregel, de somregel en de kettingregel;
de afgeleiden van exponenti&eum;le en logaritmische functies opstellen.

Verkennen

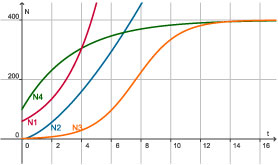
Hier zie je in één figuur vier grafieken. De bijbehorende functies zijn:

N₁(t) = 60 · 1,5^t

N₂(t) = 20 · t^1,5

N₃(t) = $\frac{400}{1 + 200 \cdot {0,5}^{t}}$

N₄(t) = 400 – 300 · 0,75^t

Elk van deze functies is te gebruiken als groeimodel.

> Beschrijf bij elk van deze functies de wijze waarop de groei verloopt.
> Beschrijf ook telkens het verloop van de groeisnelheid.

Uitleg

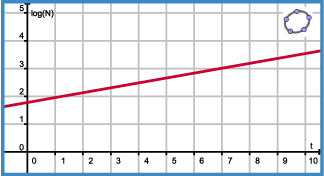
Een functie zoals N(t) = 60 · 1,5^t beschrijft exponentiële groei. Je kunt deze functie opvatten als een exponentieel groeimodel. De groei is dan nogal explosief, bij betrekkelijk kleine waarden van t heb je al met hele grote uitkomsten te maken.
Dat is lastig als je een geschikte grafiek wilt maken.
Neem je daarentegen aan beide zijden de logaritme dan krijg je: log(N) = log(60 · 1,5^t).
Met de eigenschappen van logaritmen wordt dit: log(N) = log(60) + t · log(1,5).
Omdat zowel log(60) als log(1,5) getallen zijn, staat hier dat tussen log(N) en t een lineair verband bestaat. En daarom wordt een exponentiële functie een rechte lijn als je op de verticale as een logaritmische schaal gebruikt, dus op enkellogaritmisch papier.

Een functie zoals N(t) = 20 · t^1,5 is een machtsfunctie. Ook daarvan is de grafiek lastig te tekenen, want in de buurt van t = 0 heb je uitkomsten vlak bij 0, maar bij grotere waarden van t als snel uitkomsten die behoorlijk groot zijn.
Ook nu kun je het voorschrift herschrijven m.b.v. logaritmen: log(N) = log(20 · t^1,5).
Dit levert op: log(N) = log(20) + 1,5 · log(t).
Nu bestaat er een lineair verband tussen log(N) en log(t).
Nu gebruik je op beide assen een logaritmische schaal.
Je werkt dan met dubbellogaritmisch grafiekenpapier.

‡

Opgaven

Bekijk het eerste deel van de Uitleg. Daarin gaat het over het tekenen van de grafiek van een exponentiële functie.
1. Ga na dat de getekende grafiek juist is.
Neem nu de functie `K(t) = 600 * 0,8^t`.
1. Laat op algebraïsche wijze zien dat `log(K)` een lineaire functie van `t` is.
2. Teken de grafiek van `log(K)`.
Zowel de grafiek van `N` als die van `K` kun je op enkellogaritmisch grafiekenpapier tekenen. Je hoeft dan niet eerst de formule te herschrijven.
1. Neem een blad van dit grafiekenpapier en teken daarop de grafieken van beide functies.
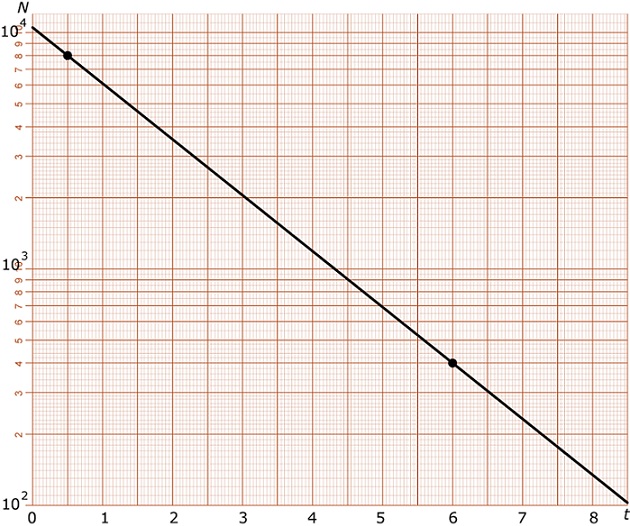
2. Je ziet hieronder de grafiek van een nieuwe functie N(t) op enkellogaritmisch grafiekenpapier. Leg uit dat de grafiek door (0,5;8000) en (6;400) gaat en stel het functievoorschrift op.
3. Lees uit de figuur af hoe groot N(1) en N(4,5) (bij benadering) zijn. Controleer je antwoorden met behulp van het functievoorschrift.
4. Heeft N(t) = 0 oplossingen? Kan er op de verticale as een 0 voorkomen?

Bekijk de functie `N_4(t) = 400 - 300 * 0,75^t`.
1. Teken de grafiek van N4 op enkellogaritmisch grafiekenpapier.
2. Kun je verklaren waarom de grafiek geen rechte lijn wordt?

Deze tabel met gegevens hoort bij een bacteriecultuur. `t` is gegeven in uren, en `N(t)` in aantallen.

t 0 1 2 3 4 5 6

N(t) 50 84 141 237 398 670 1125
1. Maak met behulp van deze tabel een tabel waarin `log(N)` wordt uitgezet tegen `t`.
2. Teken de bijbehorende grafiek. Kun je deze grafiek benaderen door een rechte lijn? Is er sprake van exponentiële groei?
3. Stel een formule op voor `log(N)` als functie van `t`.
4. Stel met behulp van het antwoord van c een formule op voor `N` als functie van `t`.

Bekijk het tweede deel van de Uitleg over het tekenen van een machtsfunctie.
1. Maak bij de functie `N` met `N(t) = 20 * t^(1,5)` een tabel van `log(N)` afhankelijk van `log(t)`. Teken de grafiek van `log(N)` uitgezet tegen `log(t)`.
2. Neem een blad dubbellogaritmisch grafiekenpapier. Teken daarop de grafiek van `N(t) = 20 * t^(1,5)`.
Neem nu de functie `K(t) = 600 * t^(0,8)`.
1. Laat op algebraïsche wijze zien dat `log(K)` een lineaire functie van `log(t)` is.
2. Teken de grafiek van `K(t)` op dubbellogaritmisch grafiekenpapier.

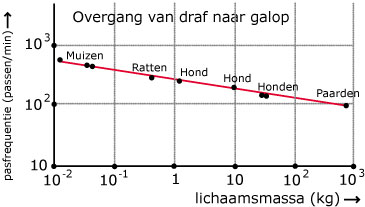Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa (in kg).
1. Waaraan kun je zien dat op beide assen van deze grafiek een logaritmische schaal is gebruikt?
2. Noem de lichaamsmassa `m` (in kg) en de pasfrequentie `P`. De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden. Leg uit dat het punt dat hoort bij paarden ongeveer de coördinaten `(10^(2,9),10^(2,0))` heeft. Bepaal zelf de coördinaten van het punt dat bij een kleine hond hoort.
3. Leid nu een formule af voor `P` als functie van `m`.
4. Bereken bij welke pasfrequentie een pony van 120 kg van draf naar galop overgaat.

Theorie

Bij het exponentiële groeimodel hoort een functie van de vorm N₁(t) = b · g^t of N₁(t) = b · e^kt of N₁(t) = b · 10^kt.
(In de figuur is b = 60 en g = 1,5.)
Teken je dergelijke functies op enkellogaritmisch papier dan wordt de grafiek een rechte lijn.

Bij een machtsfunctie als model hoort een voorschrift van de vorm N₂(t) = b · t^p.
(In de figuur is b = 20 en p = 1,5.)
Van dergelijke functies is de grafiek op dubbellogaritmisch papier een rechte lijn.

Bij een geremd exponentieel groeimodel hoort een functie als N₃(t) = $\frac{G}{1 + b \cdot g^{t}}$ .
Kenmerkend voor dit groeimodel is, dat de groei eerst vrijwel exponentieel verloopt, maar op zeker moment (voedselgebrek, te weinig ruimte) afremt. De groeisnelheid die eerst toeneemt, gaat vanaf dat moment afnemen. In dit groeimodel is N = G de horizontale asymptoot en vind je de grootste groeisnelheid bij N(t) = $\frac{1}{2}$ G.
(In de figuur is G = 400, b = 200 en g = 0,5.)

Er zijn tenslotte nog situaties waarin het verschil met een constante waarde exponentieel afneemt. Daarbij hoort een groeimodel van de vorm N₄(t) = G + b · g^t.
Kenmerkend voor dit groeimodel is dat de groeisnelheid vanaf het begin afneemt.
(In de figuur is G = 400, b = –300 en g = 0,75.)

‡

Voorbeeld 1

In deze tabel zie je de groei van een aantal fruitvliegjes ("Drosophila melanogaster"). De populatie leeft in een afgesloten ruimte met voldoende voedsel. N is het aantal fruitvliegjes.

t (dagen)	0	4	8	12	16	20	24
N(t)	2	5	10	22	47	91	156

De sterke toename van N doet exponentiële groei vermoeden.
Teken de grafiek van log(N) als functie van t en/of teken de grafiek van N(t) op enkellogaritmisch papier en stel een passende formule voor N(t) op.

Antwoord

Je kunt de grafiek maken in Excel met een logaritmische schaal op de N-as.
De rechte lijn die het beste bij deze punten past kan door Excel worden berekend (exponentiële trendlijn).
Ga zelf na, dat N(t) = 2,3 e^0,18t een passende formule is.

‡

Voorbeeld 2

Johannes Kepler (1571 - 1630) beschreef als eerste het verband tussen de omlooptijd T (in jaren) van een planeet en zijn gemiddelde afstand tot de zon R. Voor de Aarde geldt T = 1 jaar en wordt R = 1 AE (astronomische eenheid) genomen. In de tabel vind je de gegevens van de andere planeten in ons zonnestelsel.

planeet	Mercurius	Venus	Aarde	Mars	Jupiter	Saturnus	Uranus	Neptunus
R (in AE)	0,39	0,72	1	1,52	5,20	9,54	19,19	30,07
T (in jaren)	0,24	0,62	1	1,88	11,9	25,5	84,0	164,8

Het verloop van T(R) doet een machtsfunctie vermoeden.
Teken de grafiek van log(T) als functie van log(R) en/of teken de grafiek van T(R) op dubbellogaritmisch papier en stel een passende formule op.

Antwoord

Je kunt de grafiek maken in Excel met een logaritmische schaal op beide assen.
De rechte lijn die het beste bij deze punten past kan weer door Excel worden berekend (machtstrendlijn).
Ga zelf na, dat T = 1 R^1,5 een passende formule is.

‡

Voorbeeld 3

In deze tabel zie je de groei van een aantal fruitvliegjes ("Drosophila melanogaster"). De populatie leeft in een afgesloten ruimte met voldoende voedsel. N is het aantal fruitvliegjes.

t (dagen)	0	4	8	12	16	20	24	28	32	36	40	44	48
N(t)	2	5	10	22	47	91	156	226	282	317	335	343	347

Nu lijkt er sprake van geremde exponentiële groei. N(t) nadert de 350 fruitvliegjes. Stel m.b.v. de tabel een passend geremd exponentieel groeimodel op. Bereken bij welke t de groeisnelheid maximaal is.

Antwoord

De bijpassende formule wordt: N(t) = $\frac{350}{1 + b \cdot g^{t}}$ .
De grafiek gaat door (0,2) en dit geeft: b = 174.
De grafiek gaat ook door (40,335) en dit geeft: g ≈ 0,81.
Een passende formule is: N(t) = $\frac{350}{1 + 174 \cdot {0,81}^{t}}$

De waarde van t waarin de groeisnelheid een maximum heeft kun je vinden door de tweede afgeleide te berekenen en dan N"(t) = 0 op te lossen. Je kunt ook gebruik maken van het feit dat die maximale groeisnelheid bereikt wordt als N = 350/2 = 175. Je vindt in beide gevallen: t ≈ 23 dagen.

‡

Voorbeeld 4

Een kop vers gezette koffie heeft een temperatuur van 80°C. Als je die koffie rustig laat afkoelen in een omgevingstemperatuur van 20°C, dan neemt (warmtewet van Newton) het temperatuursverschil met de omgeving exponentieel af: T(t) – 20 = b · g^t.

t (min.)	0	2	4	6	8	10	12	14	16	18	20	22	24
T (°C)	80,0	58,4	44,6	35,7	30,1	26,4	24,1	22,6	21,7	21,1	20,7	20,4	20,3

Ga uit van het beschreven groeimodel en stel een bijpassende formule op.
Bereken de snelheid van afkoelen na 5 minuten.

Antwoord

Je gaat uit van: T(t) – 20 = b · g^t.
De grafiek gaat door (0,80) en dit geeft: b = 60.
De grafiek gaat ook door (24;20,3) en dit geeft: 60 · g²⁴ = 0,3 en dus g ≈ 0,80.
Een passende formule is: T(t) = 20 + 60 · 0,80^t.

De afkoelsnelheid na vijf minuten is T'(5) = 60 ln(0,80) 0,80⁵ ≈ –4,39°C/minuut.

‡

Opgaven

Bekijk Voorbeeld 1. De sterke toename van `N` doet exponentiële groei vermoeden.
1. Teken de punten uit de tabel op enkellogaritmisch papier. Teken een lijn die zo goed mogelijk past bij de getekende punten. Deze lijn stelt de grafiek van `N(t)` voor op enkellogaritmisch papier.
2. Stel zelf een formule op voor `N(t)`.
3. Controleer of de punten uit de tabel passen bij de gevonden formule.
4. Na hoeveel dagen zouden er volgens dit groeimodel meer dan 1000 fruitvliegjes zijn?

Bekijk Voorbeeld 2.
1. Teken de grafiek van `log(T)` als functie van `log(R)` en/of teken de grafiek van `T(R)` op dubbellogaritmisch papier. Wat voor soort groeimodel past bij `T(R)`?
2. Door welk punt moet je grafiek in ieder geval gaan?
3. Stel zelf een formule op voor `T(R)`.
4. In 1930 ontdekte astronoom Clyde Tombaugh een nieuw hemellichaam dat om de zon draaide op een (gemiddelde) afstand van 38,4851 AE. Dit hemellichaam werd Pluto genoemd en is lang als planeet geclassificeerd. Welke omlooptijd heeft Pluto?

In Voorbeeld 3 lijkt er sprake van geremde exponentiële groei. `N(t)` nadert de 350 fruitvliegjes.
1. Teken een grafiek van `N(t)` die zo goed mogelijk past bij de gegevens in de tabel.
2. Gebruik de grenswaarde van 350 fruitvliegjes, de waarde van N(0) en nog een ander geschikt punt van je grafiek om zelf een formule op te stellen voor `N(t)`.
3. Bereken zelf de waarde van `t` waarin de groeisnelheid van `N` zo groot mogelijk is.

Bekijk het afkoelingsproces van een kop koffie in Voorbeeld 4.
1. Ga uit van het beschreven groeimodel en stel zelf een bijpassende formule op als je aanneemt dat de grafiek door de punten `(0,80)` en (20;20,7) gaat.
2. Bereken de snelheid van afkoelen na 10 minuten.

Verwerken

De tabel geeft de gemiddelde hoogte aan van de zonnebloemen op een bepaalde akker op verschillende tijdstippen na het ontkiemen. De gemiddelde maximale hoogte die deze zonnebloemen bereiken is 256 cm.
`t` is de tijd in weken na het ontkiemen.
`H(t)` is de gemiddelde hoogte van deze zonnebloemen in cm op tijdstip `t`.

aantal weken 2 4 6 8 10 12

hoogte in cm 36 98 170 228 251 255
1. Onderzoek of er sprake is van lineaire groei, exponentiële groei, of geen van beide.
2. Beken de grafiek van de functie: `F(t) = log((256 - H(t))/(H(t)))`. Gebruik de gegevens in de tabel.
3. Toon aan dat er een eerstegraads functie is die de functie `F` redelijk benadert en geef het bijpassende functievoorschrift.
4. Leid uit de resultaten van b en c een functievoorschrift van `H` als functie van de tijd af.
5. Bereken de groeisnelheid van deze zonnebloemen op `t = 1`. Waarom is de gemiddelde groei gedurende de tweede week groter?
6. Bereken de groeisnelheid van deze zonnebloemen op `t = 10`. Waarom is de gemiddelde groei gedurende de tiende week kleiner?
7. Op welke dag na het ontkiemen van de zonnebloemen groeien ze het snelst? (Gebruik je grafische rekenmachine om het maximum van `H'(t)` te bepalen.) Hoe snel groeien de zonnebloemen dan?

In de tabel zie je de meetresultaten van een onderzoek naar het verband tussen de massa `m` van het dier en de energie `E` die het nodig heeft om zich over één kilometer te verplaatsen.

dier m (gram) E (calorieën)

muis 21 270

eekhoorn 236 870

witte ra 384 1,7 · 10³

hond (klein) 2,6 · 10³ 4,4 · 10³

hond (groot) 1,8 · 10⁴ 1,7 · 10⁴

schaap 3,9 · 10⁴ 2,3 · 10⁴

paard 5,8 · 10⁵ 5,8 · 10⁴
1. Teken deze gegevens op dubbellogaritmisch grafiekenpapier. Zet `m` uit op de horizontale as en `E` op de verticale as.
2. Waarom kun je bij benadering aannemen, dat er tussen `m` en `E` een verband van de vorm `E = a * m^b` bestaat?
3. Bereken passende waarden van `a` en `b`.
4. Bereken het energieverbruik per km van een kat met een massa van 3,2 kg.

Bij het oogsten van koren wordt vaak gewerkt met een combine, of maaidorser. In zo'n maaidorser wordt in twee etappes gedorst: eerst in de dorstrommel en daarna op de zogenaamde "schudder", waar het graan (de graankorrels) tijdens het doorlopen van een traject uit het stro wordt geschud. De snelheid waarmee de hoeveelheid graan `G` (in kg) in het stro door het schudden afneemt, is recht evenredig met die hoeveelheid zelf:
`G'(x) = -k * G(x)`
waarin `x` de afstand tot het begin van de schudder in meters is.
1. Verklaar de formule in de tekst hierboven, met name ook het minteken.
2. Toon aan dat aan deze formule een functie `G(x)` van de vorm `G(x) = b * text(e)^(-kx)` voldoet. Hierin is `b` de hoeveelheid aan het begin van de schudder.
3. Ga uit van een schudder met een totale lengte van 6 m. Neem `k = 0,2`. Hoeveel procent van de hoeveelheid graan aan het begin van de schudder is aan het einde nog niet uit het stro geschud?
4. `k` heet de scheidingsfactor van dit proces van schudden. Verklaar die naam.
5. De scheidingsfactor hangt af van de snelheid `v` (in m/s) van de maaidorser. Er geldt `k = 1/v`. Hoeveel procent van het graan wordt niet uit het stro geschud als de maaidorser rijdt met een snelheid van 2 m/s?
6. Is er een snelheid mogelijk waarbij alle graan uit het stro wordt geschud?

De volgende alinea’s zijn vrij naar een artikel dat in 1991 in een krant stond.

FAO luidt noodklok

Elk jaar verdwijnt steeds meer tropisch oerwoud. In 1990 was de afname wel anderhalf keer zo groot als in 1980. Dit stelt de FAO, de voedsel- en landbouworganisatie van de Verenigde Naties, in een zondag verschenen rapport met nieuwe gegevens over de ontbossing van de aarde.
1 — In 1990 verdween in de tropen zeventien miljoen hectare oerwoud. Dit is een gebied even groot als Oostenrijk, Denemarken en Nederland samen.
2 — Er was op 1 januari 1990 nog 2900 miljoen hectare tropisch oerwoud over.
3 — De FAO wijst naar de geïndustrialiseerde landen waar de ontbossing een halt is toegeroepen. Tussen 1 januari 1980 en 1 januari 1985 is de bosoppervlakte in die landen met 5 procent toegenomen tot 2100 miljoen hectare.

Een lezer van dit artikel probeert de gegeven informatie in een wiskundig model te verwerken om daarmee te kijken wat de gevolgen zullen zijn als de afname van het tropisch oerwoud op dezelfde wijze blijft voortduren. Zij noemt de oppervlakte aan tropisch oerwoud (in miljoenen hectare) dat op tijdstip `t` nog aanwezig is `y(t)`. Zij neemt `t = 0` op 1 januari 1980 en `t` in jaren.

Leg uit waarom zowel een formule van de vorm `y(t) = a * t + b` als een formule van de vorm `y(t) = a * g^t` niet in overeenstemming is met de gegevens uit het krantenartikel.

De lezer kiest voor een formule van de vorm `y(t) = b - a * g^t`.
Uit de in de alinea’s 1, 2 en 3 verstrekte gegevens leidt zij deze waarden af: `b = 3311`, `a = 274` en `g = 1,0414`.

Laat zien dat de formule met die waarden in overeenstemming is met de in de alinea’s 1, 2 en 3 gegeven informatie.

Wanneer de ontbossing op dezelfde wijze blijft voortduren, zal op een gegeven moment minder dan 1000 miljoen hectare tropisch oerwoud overblijven.

Bereken in welk jaar dat volgens de door de lezer gevonden formule zal gebeuren.

Het oorspronkelijke krantenartikel begon met de zin: "De tropische oerwouden verdwijnen anderhalf keer zo snel als 10 jaar geleden."

Onderzoek met behulp van differentiëren of de door de lezer gevonden formule ook hiermee in overeenstemming is.

dier	m (gram)	E (calorieën)
muis	21	270
eekhoorn	236	870
witte ra	384	1,7 · 10³
hond (klein)	2,6 · 10³	4,4 · 10³
hond (groot)	1,8 · 10⁴	1,7 · 10⁴
schaap	3,9 · 10⁴	2,3 · 10⁴
paard	5,8 · 10⁵	5,8 · 10⁴

t	0	1	2	3	4	5	6
N(t)	50	84	141	237	398	670	1125

aantal weken	2	4	6	8	10	12
hoogte in cm	36	98	170	228	251	255