Exponentiële functies

Inleiding

Je hebt het getal e leren kennen en de natuurlijke logaritme.
Je kunt nu functies van de vorm f(x) = e^x differentiëren. Maar je wilt ook f(x) = g^x en alle functies waarin g^x in het voorschrift voorkomt kunnen differentiëren. Dan kun je van dit soort functies de karakteristieken berekenen met behulp van de afgeleide en de tweede afgeleide.

Je leert nu:

de afgeleide van f(x) = g^x bepalen
de regels voor het differentiëren toepassen op functies waarin de onbekende in de exponent voorkomt;
van dergelijke functies de hellingen, de extremen en de buigpunten berekenen.

Je kunt al:

exponenten en logaritmen gebruiken;
differentiëren met alle basisregels en dit toepassen bij het berekenen van hellingen, extremen en buigpunten;
de afgeleide van f(x) = e^x bepalen.

Verkennen

Je wilt f(x) = 2^x differentiëren.
Je weet dat de afgeleide van y = e^x is y' = e^x.
Verder ken je de eigenschappen van exponenten en logaritmen.

> Leg uit waarom 2 = e^ln(2).
> Laat zien, dat f(x) = e^ln(2) · x.
> Differentieer nu f met behulp van de kettingregel.
> Welke afgeleide heeft f(x) = 2^x?

Uitleg

Je wilt f(x) = 2^x differentiëren.
Je weet dat de afgeleide van y = e^x is y' = e^x.
Verder ken je de eigenschappen van exponenten en logaritmen.

Met behulp van deze eigenschappen kun je van grondtal veranderen.
In het algemeen is g^{^glog(2)} = 2.
Dit geldt ook voor grondtal g = e, dus e^ln(2) = 2.

Hieruit volgt: f(x) = (e^ln(2))^x = e^ln(2) · x.
Nu kun je f met behulp van de kettingregel differentiëren, het grondtal is nu namelijk e.
Je vindt: f'(x) = e^ln(2) · x · ln(2).
En dit kun je weer schrijven als f'(x) = 2^x · ln(2).

Deze redenering kun je ook op elk ander grondtal toepassen. Doe je dit op grondtal g dan blijkt de afgeleide van f(x) = g^x te zijn: f'(x) = g^x · ln(g).

‡

Opgaven

In de Uitleg wordt de afgeleide van `f(x) = 2^x` bepaald.
1. Bepaal op dezelfde manier de afgeleide van `g(x) = 3^x`.
2. Bepaal op dezelfde manier de afgeleide van `h(x) = 0,5^x`.
3. Bepaal nu zelf de afgeleide van `f(x) = g^x`.

Je hebt in de voorgaande opgave de afgeleide van `f(x) = g^x` bepaald.
Ga na dat deze afgeleide ook geldt voor `f(x) = text(e)^x`.

Theorie

Voor de afgeleide van de exponentiële functie geldt:

Als f(x) = g^x dan is f'(x) = g^x · ln(g).

Hierbij maak je gebruik van het veranderen van grondtal: g = e^ln(g).
Dit is één van de definitieformules van logaritmen, toegepast op het getal e.

Hiermee kun je elke exponentiële functie N met groeifactor g per tijdseenheid t op meerdere manieren schrijven:

N(t) = N(0) · g^t
N(t) = N(0) · e^kt waarin k = ln(g)
N(t) = N(0) · 10^kt waarin k = log(g)

Dat is handig als je met meerdere exponentiële functies met verschillende groeifactoren te maken hebt. Je kunt ze dan toch steeds hetzelfde grondtal geven, e of 10.

Verder kun je nu allerlei functies waarin vormen als e^x en/of g^x voorkomen differentiëren met de differentieerregels. Daarmee kun je van functies die ingewikkelder zijn dan zuiver exponentiële functies ook de karakteristieken bepalen.

‡

Voorbeeld 1

In dit voorbeeld gaat het om het differentiëren van exponentiële functies met behulp van de differentieerregels die je tot nu toe hebt geleerd. Probeer eerst zelf de juiste afgeleiden te vinden (opgave 3) en bekijk daarna pas de oplossingen. Ga naar

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Exponentiële en logaritmische functies > Exponentiële functies > Voorbeeld 1

‡

Voorbeeld 2

Stel je voor dat je de groei van een cultuur bacteriën bestudeert. De groei hangt af van de tijd t in uren. Neem aan dat op t = 0 het aantal duizendtallen bacteriën 100 is. Verder weet je dat elke twee uur het aantal bacteriën verdubbelt. De groeifactor per uur is dus: g = 2^0,5 ≈ 1,41. Voor deze bacteriecultuur geldt de formule:

N(t) = 100 · 1,41^t

waarbij N(t) het aantal duizendtallen bacteriën na t uur is.
Bereken de groeisnelheid van het aantal bacteriën op t = 0.

Antwoord

De groeisnelheid op t = 0 is gelijk aan N'(0).
Nu is N'(t) = 100 · 1,41^t · ln(1,41) ≈ 34 · 1,41^t.
Op t = 0 bedraagt die groeisnelheid dus: N'(0) ? 34000 bacteriën per uur.
Die groeisnelheid is de richtingscoëfficiënt van de raaklijn aan de grafiek van N in t = 0. De groeisnelheid op t = 0 is kleiner dan de gemiddelde groei in het eerste uur. Die bedraagt namelijk 41000 bacteriën. Dat komt omdat de groeisnelheid gedurende dat uur voortdurend toeneemt. Aan het eind van het eerste uur is die groeisnelheid ongeveer 48000 bacteriën per uur.

‡

Opgaven

Probeer bij de functies in Voorbeeld 1 eerst zelf de afgeleiden te vinden.
Gebruik alle tot nu toe geleerde differentieerregels. Controleer pas je antwoord als je ze allemaal hebt gemaakt. Heb je fouten gemaakt? Bekijk dan goed wat je fout deed!

Bepaal de afgeleide van:
1. `f(x) = 5 * 3^x`
2. `f(x) = 5 * 2^(0,5x)`
3. `f(x) = 50 - 48 * 10^(0,1x)`
4. `f(x) = 100text(e)^(-0,1x) + 200`

Bekijk Voorbeeld 2.
1. Laat zien, dat de groeisnelheid aan het einde van het eerste uur inderdaad ongeveer 48000 bacteriën per uur bedraagt. Hoe kun je deze groeisnelheid in de grafiek aangeven?
2. Laat ook zien dat de gemiddelde groei in het eerste uur gelijk is aan 41000 bacteriën. Hoe kun je die gemiddelde groei in de grafiek van N(t) weergeven?
3. In een andere bacteriecultuur verloopt de groei wat sneller: het aantal bacteriën verdubbelt elk 1,5 uur. Op `t = 0` zijn er ongeveer 80 duizendtallen bacteriën. Welke formule geldt voor het aantal duizendtallen `M(t)` bacteriën in deze cultuur?
4. Bereken algebraïsch het tijdstip waarop beide bacterieculturen evenveel bacteriën bevatten.
5. Bereken ook de groeisnelheid van beide bacterieculturen op het tijdstip waarop beide evenveel bacteriën bevatten.

Differentieer de volgende functies en stel de vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 1`.
1. `f(x) = 4 * 3^(2x - 4) - 12`
2. `f(x) = (text(e)^(2x) - 1)/(text(e)^x)`

Bij benzinestations is vaak een extra service beschikbaar om de autobanden op te pompen. De automatische pomp levert een druk van 3,5 atmosfeer. De luchtdrukverandering in de band is recht evenredig met het drukverschil tussen de luchtdruk in de band en de luchtdruk van de pomp. De luchtdruk in de band begint met 1,4 atmosfeer en is na 10 seconden pompen opgelopen tot 2,0 atmosfeer.
1. De luchtdruk `p` in de band (in atmosfeer) hangt gedurende het oppompen af van de tijd `t` in seconden. Schets een passende grafiek bij dit verband.
`p(t)` kan worden beschreven door een formule van de vorm: `p(t) = 3,5 - a * g^t`.
1. Bereken `a` en `g`.
2. Je stopt de pomp als de druk in de band 2,6 atmosfeer bedraagt. Na hoeveel seconden is dat het geval?
3. Bereken de snelheid waarmee de druk in de band toeneemt op `t = 0`.

Zowel in de atmosfeer als in levende organismen bevindt zich een bepaald percentage aan radioactieve koolstof C-14. Zodra een organisme sterft vindt er geen uitwisseling met de koolstof uit de atmosfeer meer plaats. Het percentage C-14 neemt vanaf dat moment exponentieel af met een halveringstijd van ongeveer 5600 jaar. Omdat alle levende organismen eenzelfde gehalte aan C-14 hebben, stelt dit ons in staat de ouderdom te bepalen van natuurlijke materialen als perkament, leren kleding, houten palen en dergelijke.
Het gehalte `C(t)` aan C-14 is gegeven als percentage van het gehalte in levende organismen. `t` is de tijd in jaren met `t = 0` op het moment dat het organisme is gestorven.
1. Stel een formule op voor `C(t)` van de vorm `C(t) = 100 * text(e)^(kt)`. Bereken `k` in zes decimalen nauwkeurig.
2. Van de Dode-Zeerollen is het gehalte aan C-14 nog 79%. Hoe oud zijn ze?
3. Van een mummie is nog 65% van het gehalte aan C-14 over. Hoe oud is die mummie?
4. Van een Indianensandaal uit een grot in Amerika is nog 33% van het gehalte aan C-14 over. Hoe oud is die sandaal?

Verwerken

Bekijk de grafiek van de functie `f` met `f(x) = x + 2^(-x)`.
1. Bereken het minimum van de grafiek van `f` in twee decimalen nauwkeurig.
2. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 0`.

Als je melk niet in de koelkast bewaart, gaat ze rotten onder invloed van bacteriën die saprofieten heten. Stel je voor dat op zeker moment (`t = 0`) het aantal saprofieten in een vol literpak melk 200 bedraagt. Een uur later blijken het er zo’n 350 te zijn. Op het moment dat er zo’n 100 000 saprofieten in een liter melk zitten is die melk ondrinkbaar geworden. Neem aan dat er sprake is van exponentiële groei, waarin `N(t)` het aantal saprofieten is na `t` uur.
1. Stel een passend exponentieel groeimodel op.
2. Bereken de groeisnelheid op `t = 0`. Waarom ligt het afronden op tientallen voor de hand?
3. Maak met behulp van die groeisnelheid op `t = 0` een schatting van het aantal saprofieten op `t = 1`. Leg uit hoe je dat doet en bereken het verschil met het werkelijke aantal saprofieten. Rond steeds af op tientallen.
4. Bereken na hoeveel tijd de melk ondrinkbaar is geworden.

Melk bewaar je in de koelkast op een temperatuur van 6°C. Als je een glas melk inschenkt heeft dit op `t = 0` dan ook deze temperatuur. Vanaf dat moment warmt de melk op tot kamertemperatuur, zeg 20°C. Die opwarming gaat volgens de warmtewet van Newton zo, dat de snelheid van opwarmen recht evenredig is met het temperatuursverschil met de omgeving.
1. Maak een schets van het verloop van de temperatuur `T` van de melk als functie van de tijd `t` in minuten.
2. Leg uit dat de functie `T` die de temperatuur van de melk in het glas beschrijft moet voldoen aan `T'(t) = c * (T(t) - 20)`.
3. Toon aan dat een functie van de vorm `T(t) = 20 + a * text(e)^(ct)` voldoet.
4. Neem aan, dat na 12 minuten de melk is opgewarmd tot 18°C. Stel een daarbij passende formule voor `T(t)` op.
5. Bereken de opwarmsnelheid van de melk op `t = 0` en op `t = 15`. Verklaar het verschil tussen beide waarden.

Een forellenkweker zet in elk van zijn kweekvijvers steeds 5000 jonge forellen uit. Die forellen nemen vanaf dat moment (`t = 0`) in gewicht toe, maar er sterven ook forellen. Hij heeft al een aantal jaren maandelijks de stand van de forellen bijgehouden. Op grond daarvan kan hij formules opstellen voor de groei van zo'n populatie forellen. Als `t` de tijd in maanden is, dan geldt:
- `N(t) = 5000 * text(e)^(a * t)` waarin `N` het aantal forellen is.
- `G(t) = G_(text(eind)) - b * text(e)^(c * t)` waarin `G` het gewicht per forel in kg is.
`G_(text(eind))` stelt het gewicht voor dat een gemiddelde forel steeds meer zal benaderen naarmate hij ouder wordt.
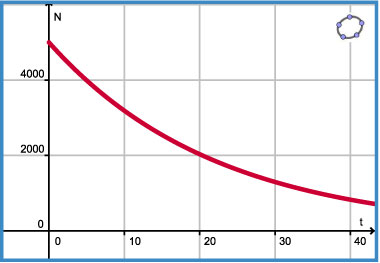
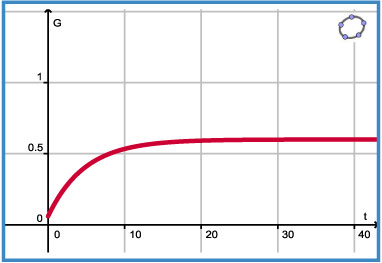
1. De uitgezette forellen wegen gemiddeld 65 gram. Stel nu met behulp van de grafieken de juiste formules op voor `N(t)` en `G(t)`.
2. Stel een formule op voor het totale gewicht aan forellen in deze vijver.
3. Als de forellenkweker zijn kweekvijver wil leegvissen als het totale gewicht aan forellen maximaal is, hoeveel maanden na het uitzetten moet hij dat dan doen?

Testen

Differentieer de volgende functies en stel een vergelijking op van de raaklijn aan de grafiek van `f` in het snijpunt met de `x`-as.
1. `f(x) = 3 * 0,5^(2x - 1) - 4`
2. `f(x) = 5 - text(e)^(sqrt(x))`

Bij het maken van foto’s van je gebit gebruikt de tandarts röntgenstraling. De patiënt krijgt een heel geringe dosis straling toegediend en ondervindt daarvan geen nadelige gevolgen. Maar een tandarts die dit regelmatig doet krijgt te maken met een opeenhoping van straling in zijn lichaam. Daarom beschermt hij zich met behulp van een loden plaat.
De intensiteit van de straling neemt namelijk af in een stof als lood. Als die stralingsintensiteit wordt voorgesteld door `I`, dan geldt:
`I(d) = I(0) * text(e)^(-alpha * d)`
waarin `d` de dikte van de loden plaat in cm is en `alpha` een constante is die afhangt van het materiaal.
1. Een loden plaat van 1 cm dik houdt ongeveer 60% van de straling tegen. Bereken de materiaalconstante `alpha`.
2. Hoe dik moet een loden plaat zijn om 99% van de straling tegen te houden?
3. Hoeveel bedraagt de snelheid waarmee de stralingsintensiteit afneemt op het moment dat die straling de loden plaat bereikt?