Noodzakelijke differentieerregels

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Exponentiële en logaritmische functies > Differentieerregels > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Exponentiële en logaritmische functies > Differentieerregels > Uitleg

Opgaven

  1. Lees eerst de Uitleg goed door. Bekijk de grafiek van de functie `f(x) = text(e)^(3x)` op de grafische rekenmachine. Breng ook een benadering van de grafiek van `f'` en hun verhouding in beeld. Gebruik de standaardinstellingen van het venster.
    1. Ga na dat voor een willekeurige `x` de waarden van de afgeleide 3 keer zo groot zijn dan die van de functie zelf. Wat is de afgeleide van `f`?
    2. Bekijk nu het functievoorschrift. Uit welke twee schakels bestaat het?
    3. Laat zien hoe je deze afgeleide met de kettingregel bepaalt.

  2. Bekijk de grafiek van de functie `f(x) = text(e)^(x^2)` op de grafische rekenmachine. Breng ook een benadering van de grafiek van `f'` in beeld. Kies het venster zo dat `x` loopt vanaf `-2` tot en met `2` en `y` vanaf `-10` tot en met `10`.
    1. Bepaal de afgeleide van `f` met behulp van de kettingregel.
    2. Voer deze afgeleide ook in je grafische rekenmachine in en ga na dat de grafiek (bij benadering) samenvalt met de eerder gemaakte benadering van `f'`.

  3. Neem `f(x) = sqrt(x)`.
    Deze functie kun je met de machtsregel differentiëren omdat `f(x) = sqrt(x) = x^(1/2)`.
    Laat zien dat de afgeleide wordt: `f'(x) = 1/(2 sqrt(x))`.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Exponentiële en logaritmische functies > Differentieerregels > Theorie

Bestudeer eerst de Theorie. De hier genoemde differentieerregels komen uitgebreid bij wiskunde B aan de orde. In de opgaven wordt je naar de Voorbeelden verwezen en worden de differentieerregels vooral toegepast op e-machten.

Opgaven

  1. Bekijk Voorbeeld 1. Stel de applet in op `f_(0,5)(x) = text(e)^(0,5x)`.
    1. Het punt `(1,e)` op de grafiek van `f_1(x) = text(e)^x` gaat door het vervangen van `x` door `0,5x` over in een ander punt. Welk punt?
    2. Hoe zit het met de helling van de grafiek van `f_(0,5)` in dit punt vergeleken met de helling van de grafiek van `f_1` in `(1,e)`?
    3. Bepaal nu met de behulp van de kettingregel de afgeleide van `f_(0,5)`.
    4. Komt deze afgeleide overeen met het antwoord van b?

  2. Differentieer de functies:
    1. `f(x) = text(e)^(5x)`
    2. `g(x) = 15text(e)^(6 - 2x) + 12`
    3. `h(x) = 12text(e)^(-0,5x^2)`
    4. `k(x) = 40 - 6text(e)^(x^3-1)`

  3. Bekijk Voorbeeld 2. Neem `f(x) = 1/x`.
    1. Schrijf het functievoorschrift als machtsfunctie (met een negatieve exponent).
    2. Laat zien, dat `f'(x) = - 1/(x^2)`.

  4. Differentieer de volgende functies en schrijf de afgeleide zonder gebroken en/of negatieve exponenten:
    1. `f(x) = 3/(x^2)`
    2. `g(x) = x sqrt(x)`
    3. `h(x) = 4/(sqrt(x))`
    4. `k(x) = 5 sqrt(x) - 1/(2 sqrt(x))`

  5. In Voorbeeld 3 zie je nog eens hoe je de vergelijking opstelt van de raaklijn aan de grafiek van een gegeven functie voor een bepaalde waarde van `x`.
    1. Bepaal zelf de afgeleide van de gegeven functie `f`.
    2. Laat zien hoe je de vergelijking van de raaklijn aan `f` voor `x = 1` opstelt.
    3. Voor `x = p` gaat de raaklijn aan de grafiek van `f` door de oorsprong van het assenstelsel. Bereken `p`.

  6. Bepaal de afgeleide van de volgende functies en schrijf hem zonder gebroken en/of negatieve exponenten:
    1. `f(x) = text(e)^(2 sqrt(x))`
    2. `g(x) = 1/(2x) - text(e)^(2x)`
    3. `h(x) = 3sqrt(x) + text(e)^(2x)`
    4. `k(x) = text(e)^(x^2) - 3/(text(e)^(2x))`

Verwerken

  1. Differentieer de volgende functies:
    1. `f(x) = text(e)^(2x) - 3sqrt(x)`
    2. `g(x) = 3/(5x^2) + text(e)^(sqrt(2x))`
    3. `h(x) = 50/(1 + 3text(e)^(-0,5x))`
    4. `k(x) = 20 + 60 * text(e)^(-0,8x)`

  2. Gegeven is de functie `f` met `f(x) = 2x - text(e)^(3x)`.
    1. Bepaal de afgeleide van `f`.
    2. Bereken de exacte waarde van het maximum van `f` met behulp van de afgeleide.
    3. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 1`.

  3. Als een kabel tussen twee masten aan beide uiteinden op dezelfde hoogte wordt opgehangen, dan neemt hij de vorm aan van een zogenaamde "kettinglijn". Neem aan dat beide masten 60 m uit elkaar staan. Dan past bij die kettinglijn een formule als:

    `h(x) = 0,05(text(e)^(0,15x) + text(e)^(-0,15x)) + 10`

    waarin `h` de hoogte boven de grond is. `x` en `h` zijn beide in meter, de ophangpunten zitten bij `x = 30` en `x = –30`.



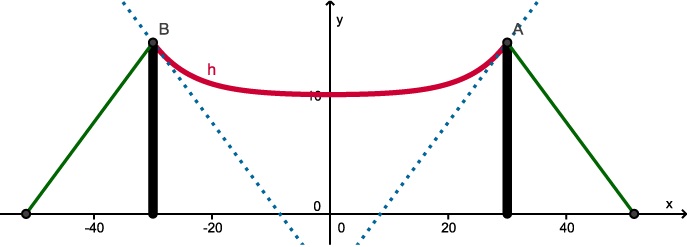
    1. Op hoeveel m boven de grond is deze kabel opgehangen?
    2. Hoeveel afstand zit er tussen twee punten van de kabel die 12 m boven de grond zitten?
    3. Toon met behulp van differentiëren aan dat het laagste punt van deze kabel bij `x = 0` zit.
    4. Er worden twee lijnen gespannen die de masten waaraan de kabel is opgehangen verticaal houden. Deze lijnen maken dezelfde hoek met de masten als de kabel in de ophangpunten. Welke hoek is dat? Geef je antwoord in tienden van graden nauwkeurig en maak gebruik van de afgeleide van `h`.

Testen

  1. Differentieer de volgende functies en stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x = 2`.
    1. `f(x) = 0,1text(e)^(sqrt(x))`
    2. `f(x) = 2/(text(e)^(0,5x))`
    3. `f(x) = -5 + text(e)^(x - 2)`

  2. Gegeven is de functie `f` met `f(x) = 0,5 text(e)^(-x) - 2`.
    1. Welke asymptoot heeft de grafiek van deze functie?
    2. Bereken algebraïsch het snijpunt van de grafiek van `f` met de `x`-as. Geef een benadering in drie decimalen nauwkeurig.
    3. Stel een vergelijking op van de raaklijn aan de grafiek van `f` in dit punt.
    4. Los algebraïsch op: `f(x) < 4`. Geef een benadering in drie decimalen nauwkeurig.