Modelleren

Inleiding

Een model is een vereenvoudiging van de werkelijkheid waarin nog alle eigenschappen zijn terug te vinden die belangrijk zijn voor het probleem.
Het verband tussen de kijkafstand a (in m) in een aards lanschap zonder obstakels en de hoogte h (in m) is daarvan een voorbeeld. De formule $a=3572\cdot h^{\frac{1}{2}}$ kun je zelf afleiden. Het proces van het bedenken van zo'n rekenmodel voor de situatie is modelleren.

Je leert nu:

• werken met wiskundige modellen in eenvoudige situaties;
• welke stappen er bij het construeren van een wiskundig model zijn te herkennen;
• hoe je het stellen van goede vragen kunt gebruiken om een model te construeren.

Je kunt al:

• werken met formules en evenredigheid;
• eenvoudige meetkunde uit de onderbouw.

Verkennen

Iemand staat op een vlot midden op een rustige (vlakke) zee. Hoe ver kan hij kijken?

> Probeer zelf een oplossing te verzinnen.

Uitleg

Een model is een vereenvoudiging van de werkelijkheid waarin nog alle eigenschappen zijn terug te vinden die belangrijk zijn voor de beschrijving van een bepaald verschijnsel dat je wilt verklaren. Het bewust opstellen van zo地 model noem je modelleren.
Bij het modelleren volg je een aantal vaste stappen.
In de videoclip vind je een beschrijving daarvan, vergelijk die met de Theorie. Bekijk eerst de videoclip via

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Toegepaste analyse > Modelleren > Modelleren > Uitleg

‡

Opgaven

1. Bekijk het probleem bij Verkennen. Heb je zelf een oplossing gevonden?
   1. Waarom kan hij niet oneindig ver kijken ook als er geen obstakels in de weg staan?
   2. Maak een schets van de situatie. Houd daarbij rekening met de vorm van het aardoppervlak.
   3. Hoe heb je in je figuur de afstand die hij kan kijken aangegeven?
   4. Welke vereenvoudigingen heb je nu al toegepast?
   Waarschijnlijk bestaat je figuur uit een (deel van een) cirkel die een doorsnede van het aardoppervlak voorstelt met daarop een lijnstukje dat de persoon die kijkt voorstelt. Als dat niet zo is, maak dan alsnog een dergelijke figuur. Noem het middelpunt van de cirkel `M` en het lijnstuk (dat degene die kijkt voorstelt) `PQ`, met `Q` op het aardoppervlak.
   5. Waarom moet `PQ` liggen op het verlengde van `MQ`?
   6. Punt `R` is een punt op het aardoppervlak dat de persoon die kijkt nog net kan zien. Geef zo地 punt in je figuur aan.
   7. Welke eigenschap heeft driehoek `MPR`? Probeer daar een verklaring voor te vinden.
   8. De omtrek van de aarde is 40.000 km. Van welke lijnstukken kun je nu de lengte berekenen?


2. Iemand doet nu het volgende voorstel om het probleem op te lossen:
   Kies voor de lengte van `PQ` (de lengte van de persoon die kijkt) een bepaalde waarde, bijvoorbeeld 1,80 m. Verder is de kijkafstand `PR` en die geef je de letter `a`. Vervolgens pas je de stelling van Pythagoras toe in driehoek `MPR`.
   1. Je kunt daarmee `a` uitrekenen. Doe dat.
   2. De lengte van de persoon die kijkt hoeft niet 1,80 m te zijn. Hoe kun je daarmee rekening houden?
   3. Probeer nu een volledige oplossing van het probleem te beschrijven. Je kunt daarbij werken met variabelen en een formule. Maar je kunt ook werken met de computer en een rekenblad als Excel.


3. Iemand anders doet een iets ander voorstel:
   Kies voor de lengte van `PQ` (de lengte van de persoon die kijkt) de variabele `h`. Verder is de kijkafstand de lengte van de boog `QR` en die geef je de letter `a`. De lengte van die boog wordt bepaald door de grootte van hoek `QMR`. En die kun je uitrekenen in driehoek `MPR`.
   1. Beschrijf nu hoe je `a` kunt berekenen.
   2. Waarom is nu het probleem opgelost?
   3. Welke van beide modellen (zie opgaven 3 en 4) vind je het beste?

Theorie

Een model is een vereenvoudiging van de werkelijkheid waarin nog alle eigenschappen zijn terug te vinden die belangrijk zijn voor de beschrijving van een bepaald verschijnsel dat je wilt verklaren. Het bewust opstellen van zo地 model noem je modelleren.
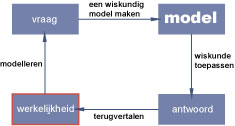
Bij het modelleren volg je een viertal vaste stappen.

1. Je kijkt naar de werkelijkheid en stelt jezelf een vraag: de probleemstelling. Je bedenkt welke grootheden, welke variabelen een rol spelen.
2. Je vereenvoudigt de werkelijkheid door aannames te doen en ontwerpt een wiskundig model dat zo goed mogelijk bij de probleemstelling past. Geef duidelijke definities van de grootheden waartussen je verbanden gaat zoeken. Je moet je ook goed bijhouden waarom je bepaalde dingen weglaat.
3. Je zoekt het antwoord op je vraag door in je model wiskundige berekeningen toe te passen. Het antwoord kan de oplossing van het probleem zijn, maar ook een beschrijving van de bepaalde situatie.
4. Je kijkt of je antwoord wel past bij de werkelijkheid. Je moet je antwoord "terug vertalen". Als dat kan ontwerp je ook een test. Daarmee onderzoek je of je model goed genoeg was of moet worden bijgesteld en doorloop je de cyclus opnieuw.

‡

Voorbeeld 1

Iemand staat op het strand aan de waterlijn. Schuin voor zich ziet hij een zwemmer in nood. Hoe kan hij zo snel mogelijk bij de zwemmer komen om hulp te bieden? Springt hij meteen in het water of loopt hij eerst een stuk langs het strand?

Iemand heeft een figuur gemaakt waarbij punt A de persoon aan de waterlijn voorstelt, punt Z de zwemmer in nood en ABZ een rechthoekige driehoek is waarvan AB de waterlijn voorstelt. Hij neemt aan dat AB = 400 m en dat BZ = 200 m. De loopsnelheid neemt hij (bij hard lopen) 10 km/uur en de zwemsnelheid 2 km/uur.

‡

Voorbeeld 2

Griep is een besmettelijke ziekte die van mens tot mens wordt overgedragen. Als de griep opduikt is er sprake van gezonde mensen, zieke mensen en mensen die ziek zijn geweest maar beter zijn geworden. Alleen zieke mensen steken gezonde mensen aan. De gemiddelde ziekteduur is 4 dagen, daarna ben je geruime tijd immuun geworden. Je begint op een bepaalde dag met 100.000 personen waarvan er 100 ziek en 500 immuun zijn. Hoe verloopt het aantal zieken per dag, hoeveel is dit maximaal?
Probeer zelf een model voor het ziekteverloop te verzinnen.

‡

Voorbeeld 3

Op diverse plaatsen in Nederland zijn windmolens geplaatst op energie op te wekken. Het vermogen van zo'n windmolen hangt af van de grootte van de wieken en de windsnelheid. Je kunt er dit wiskundige model voor opstellen.
Het opgewekte vermogen is recht evenredig met de kinetische energie van de luchtstroom die per uur voorbij komt:
P = c · m · v²
waarin P het vermogen in kiloWattuur (KWh), m de massa van de hoeveelheid lucht per seconde en v de windsnelheid in meter per seconde (m/s) is.

De hoeveelheid lucht die per seconde voorbij komt is een cilinder met een grondvlak van 1 4 πD² en een lengte van v.
De massa daarvan is 1 4 πD² · v · ρ waarin ρ de dichtheid van de lucht is, het aantal kg per m³.

Zo vind je P = c · 3600 ·  1 4 πD² · v · ρ · v² = C · v³ · D².

De constante C hangt af van de dichtheid van de lucht, de eigenschappen van de windmolen, e.d. Hij is alleen experimenteel te bepalen, door metingen te verrichten dus.

‡

Opgaven

4. Bekijk de opgaven bij de Uitleg over het probleem van de kijkafstand nog eens. Leg de modelcyclus zoals die in de Theorie is beschreven er naast.
   1. Welke grootheden kende dit probleem? Wat is het verschil tussen een grootheid en een variabele?
   2. Welke aannames heb je allemaal gedaan?
   3. Hoe heb je de kijkafstand in een schets aangegeven? Welke definitie van kijkafstand geef je daarmee? (Er zijn twee mogelijkheden bekeken.)
   4. Heb je de kijkafstand van tevoren kunnen schatten? Welk nut heeft zo地 schatting?
   5. Waarom is de vraag naar de eigenschappen van driehoek MPR heel belangrijk?
   6. Over welke stap van de modelleercyclus gingen de voorgaande vragen?
   7. Hoe gebruik je de rechthoekige driehoek in de mogelijke uitwerkingen?
   8. Welke voorkennis had je nodig?
   9. Over welke stap in de modelcyclus gingen de vragen g en h?
   10. Hoe maak je de uitwerking zo algemeen mogelijk (verschillende kijkhoogtes)?
   11. Wat doe je in de vierde stap van de modelleercyclus bij dit probleem?
   12. Hoe kun je het model van de kijkafstand testen in de praktijk?


5. In Voorbeeld 1 zie je het probleem van het bepalen van de kortste weg naar een drenkeling.
   1. Probeer zelf een oplossing te verzinnen.
   Hierna word je aan de hand van hulpvragen naar de oplossing geleid. Gebruik de aannames in het voorbeeld.
   2. Waarom is het waarschijnlijk verstandig om eerst een stuk langs het strand te lopen?
   3. Probeer aan de hand van de opmerkingen in het voorbeeld een schets te maken van de situatie. Neem aan dat je vlak langs de waterlijn kunt lopen en dat die waterlijn recht is.
   4. Hoeveel tijd kost dan het bereiken van de zwemmer als er alleen wordt gezwommen?
   5. En hoeveel tijd kost het bereiken van de zwemmer als het hele stuk `AB` eerst wordt gelopen en dan `BZ` wordt gezwommen?
   6. Denk je dat er een keuze mogelijk is die minder tijd kost? Hoe dan? Kun je nu het probleem verder zelf oplossen?


6. Misschien heb je bij de vorige opgave al bedacht dat een kortere afstand wordt bereikt als de persoon bij `A` niet helemaal van `A` naar `B` loopt, maar slechts een deel `AP` van die afstand.
   1. Kies een waarde voor AP en bereken dan de tijd die nodig is om de zwemmer te bereiken.
   2. Beschrijf de rekenprocedure als je verschillende waarden voor `AP` wilt kunnen kiezen.
   3. Zijn de aannames voor de lengtes en de afstanden handig gekozen? Kun je dit verbeteren zonder het rekenmodel te verknoeien?
   Je kunt ook werken met een variabele voor de lengte van `AP`. Noem die lengte bijvoorbeeld `x`.
   4. Stel een formule op voor de totale tijd die nodig is om `Z` te bereiken vanuit `A`.
   5. Hoe kun je het probleem verder oplossen?
   6. Hoe controleer je het antwoord?
   7. Probeer nu het complete model (inclusief de aannames) duidelijk te beschrijven.
   8. Probeer het model nog verbeteren door de lengtes en snelheden ook variabel te maken. Je kunt dit doen door de formules aan te passen. Je kunt dit ook doen met behulp van een rekenblad in Excel.


7. Bekijk de opgaven hiervoor bij "Zwemmer in nood" nog eens.
   1. Welke aannames heb je gedaan?
   2. Hoe heb je die in de schets van de situatie verwerkt?
   3. Welke extreme gevallen heb je eerst doorgerekend?
   4. Welke variabele heb je ingevoerd? Kon je ook een andere variabele kiezen?
   5. Welke verbanden tussen de variabelen heb je gevonden?
   6. Kun je het antwoord controleren? Beschrijf een mogelijke test (zonder dat je een zwemmer in nood moet inschakelen)?
   7. Maak nu een overzicht van wat je bij elke stap van de modelcyclus hebt gedaan om dit probleem op te lossen.


8. Bekijk in Voorbeeld 2 het probleem van de griepepidemie.
   1. Probeer zelf een model voor het ziekteverloop te verzinnen. Schakel eventueel de computer en het rekenblad Excel in.
   Hierna word je aan de hand van hulpvragen naar een oplossing geleid.
   2. Welke drie grootheden kent dit probleem behalve de tijd in dagen?
   3. Er bestaan verbanden tussen die drie variabelen. Kun je die weergeven in een schema (met pijlen)?
   4. Waarom wordt gemiddeld elke dag 25% van de zieken weer gezond (en dus immuun)?
   5. Neem aan, dat dagelijks een bepaald percentage van de zieken een gezond iemand aansteekt. Kies een vast percentage. Geef de percentages in je pijlenschema weer.
   6. Heb je bij je eigen oplossing ook zo地 aanname gedaan?
   Werk nu verder met de aanname die in e is gedaan. Op `t = 0` heb je 5000 zieken, 10.000 personen die immuun zijn en dus 85.000 gezonden. Hierin is `t` de tijd in dagen.
   7. Hoeveel zijn dat er op `t = 1` en op `t = 2`?
   8. Hoe reken je nu verder? Krijg je realistische uitkomsten?


9. Iemand bedenkt nu het volgende:
   `G(t)` is het aantal gezonde personen op zeker tijdstip `t`.
   `Z(t)` is het aantal zieken en `I(t)` is het aantal immune personen.
   Een dag later zit je op tijdstip `t + 1`.
   Dan is: `G(t + 1) = G(t) - 0,2 * Z(t)`.
   1. Leg deze formule uit. Hoe groot is bij hem de kans dat een zieke iemand anders ziek maakt?
   2. Welke formule geldt nu voor `Z(t + 1)` als elke dag 25% van de zieken beter wordt en er gezonde mensen ziek worden volgens de voorgaande formule?
   3. Welke formule geldt er voor `I(t + 1)`?
   4. In een rekenblad in Excel kun je dat in formules verwerken. Bekijk de figuur.
      
      
      
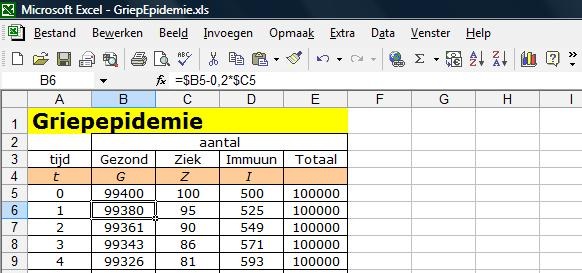
      In cel B6 staat de formule =$B5-0,2*$C5.
      Leg uit dat dit overeen komt met de formule `G(t + 1) = G(t) - 0,2 * Z(t)`.
      Wat staat er in cel C6? En in cel D6?
   5. Hoe gaat de griepepidemie verlopen? Maak een tabel met je grafische rekenmachine of gebruik het rekenblad Excel.
   6. Hoe zit het nu met het maximale aantal zieken? Lijkt het model erg realistisch?


10. Bij nader inzien lijkt het hiervoor beschreven model voor de griepepidemie niet goed te zijn: het aantal personen dat ziek wordt gemaakt door iemand die al ziek is hangt natuurlijk vooral af van het aantal gezonde mensen (alleen die kunnen nog ziek worden). Dat zal geen vast percentage van het aantal zieken zijn. Dit hangt eerder af van het percentage gezonde mensen waarmee een zieke in contact komt en de kans dat dan ook de ziekte wordt overgedragen.
    1. Het rekenblad in Excel wordt daarom wat aangepast. In cel C6 komt nu =$C5-0,25*$C5+0,02*0,5*$B5. Hieruit blijkt dat de kans dat de ziekte wordt overgedragen van een zieke op iemand die gezond is op 50% is gesteld. Hoe groot is het percentage gezonde mensen waarmee een zieke in contact komt volgens dit model?
    2. Schrijf nu de drie bijbehorende modelformules op.
    3. Hoe gaat de griepepidemie verlopen? Maak een tabel met je grafische rekenmachine of met het rekenblad Excel.
    4. Lijkt dit model realistischer? Of zou je nog aanpassingen willen aanbrengen? En zo ja, welke dan?
    5. Kun je een manier verzinnen om het model te testen?


11. Bekijk de opgaven hiervoor bij "Griepepidemie" nog eens.
    1. Welke aannames heb je gedaan?
    2. Waarom is het nuttig om een graaf (een schema met pijlen) kunnen maken van de situatie?
    3. In het eerste model (opgave 10) werd er van uit gegaan dat dagelijks een bepaald (vast) percentage van de zieken een gezond iemand ziek maakt. Hoe zit dat in het model verwerkt?
    4. Waarom lijkt die aanname niet te kloppen op grond van de resultaten van opgave 10? Is er nog een andere reden waarom die aanname niet zal kloppen?
    5. Hoe wordt het model bijgesteld? Wordt daarbij de gehele modelcyclus opnieuw doorlopen?
    6. Kun je een manier bedenken om het model verder te testen?
    7. Maak nu een overzicht van wat je bij elke stap van de modelcyclus hebt gedaan om dit probleem op te lossen.


12. Bestudeer Voorbeeld 3. Hierin gaat het om een formule voor het vermogen van een windmolen.
    1. Welke aannames zijn er gedaan?
    2. Welke natuurkundige en wiskundige voorkennis is nodig?
    3. Hoe wordt daarbij de modelcyclus doorlopen?
    4. Kun je een manier bedenken om het model te testen?

Verwerken

13. Je staat ergens op aarde stil, bijvoorbeeld in het centrum van Amsterdam. Hoe snel beweeg je als gevolg van het draaien van de aarde?
    Stel hiervoor zelf een model op. Maak daarbij gebruik van de modelcyclus. Probeer een manier te verzinnen om het model te testen.
    


14. Je kent ze wel: de treintjes van M舐klin of Fleischmann. Je ziet er hier 鳬ntje die staat op de drijfstang van hetzelfde origineel. Neem aan dat een echte loc met een snelheid van 60 km/h rijdt. Hoe snel moet je het schaalmodel laten rijden om het "echt" te laten lijken?
    Los dit probleem op volgens de modelcyclus.
    


15. Een bosbouwer verkoopt hout van bomen die hij zelf aanplant. Stel je voor dat hij op een bepaald stuk bos ongeveer 5000 bomen heeft geplant. Na een aantal jaren zijn de eerste bomen groot genoeg om te kunnen worden gekapt. Maar om ook daarna elk jaar opbrengst van dit perceel te hebben zal hij
    • de meeste bomen moeten laten staan;
    • nieuwe bomen aanplanten.
    Hij besluit elk jaar 15% van de bomen te kappen en dan weer 1000 aan te planten. Hij plant dus meer aan dan hij kapt, teneinde de opbrengst te verhogen. Op dit perceel is namelijk wel ruimte voor zo地 6000 bomen.
    1. Onderzoek hoe het aantal bomen dat er jaarlijks op dit perceel staat, gaat verlopen. Maak een grafiek.
    2. Zal het aantal bomen de 6000 gaan overstijgen, denk je?