Normale toetsen

Inleiding

Het toetsen van hypothesen kun je ook doen als een stochast normaal is verdeeld.
een goed voorbeeld is de controle door de consumentenbond van het vulgewicht van kilopakken suiker. Ook daarbij speelt de significantie een grote rol. Maar bovendien wordt er vaak een steekproef getrokken met een bepaalde grootte n uit een normaal verdeelde populatie. En dan moet je met de wortel-n-wet rekening houden.

Je leert nu:

• het gemiddelde μ van een normaal verdeelde stochast toetsen;
• de wortel-n-wet gebruiken bij een steekproef van grootte n.

Je kunt al:

• werken met binomiale toetsen;
• de begrippen nulhypothese, alternatieve hypothese en beslissingsvoorschrift en significantieniveau gebruiken.

Verkennen

Volgens de fabrikant is het gewicht G (in gram) van zijn pakken suiker normaal verdeeld met μ(G) = 1002 en σ(G) = 3.
Omdat de consumentenbond veel klachten heeft binnengekregen waarin wordt gemeld dat de pakken suiker van deze fabrikant te weinig suiker bevatten, wordt er door hen getwijfeld aan dit gemiddelde. De consumentenbond stelt dat μ(G) < 1002.
Ze onderzoeken de bewering van de fabrikant door een pak suiker te wegen.
Ze vinden dat de fabrikant ongelijk heeft als dit pak suiker minder dan 998 gram weegt.

> Hoe groot is de kans dat men toevallig minder dan 998 gram suiker vindt?
> Wat zegt dit over de kans dat de consumentenbond een fout maakt?
> Hoe zou de consumentenbond dit resultaat kunnen verbeteren?

Uitleg

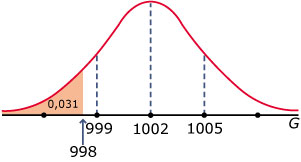Bekijk het probleem hierboven nog eens.
De consumentenbond vindt dat de fabrikant ongelijk heeft als dit pak suiker minder dan 998 gram weegt.
Dan bestaat de kans dat dit pak toevalligerwijs minder dan 998 gram weegt, terwijl toch de fabrikant gelijk heeft. De consumentenbond zou dan moeten beweren dat de fabrikant ongelijk heeft, terwijl dat niet waar is.
Ga na, dat die kans is: P(G < 998 | μ = 1002 en σ = 3) ≈ 0,091.
Er is dus meer dan 9% kans dat de consumentenbond ten onrechte beweert dat de fabrikant ongelijk heeft.

De bewering van de fabrikant is: het gewicht G (in gram) van mijn pakken suiker is normaal verdeeld met μ(G) = 1002 en σ(G) = 3. Dit heet de nulhypothese en wordt aangeduid met H₀.
De consumentenbond stelt dat μ(G) < 1002. Dat is de alternatieve hypothese H₁.

Om te toetsen of de bewering van de fabrikant juist is doet de consumentenbond een steekproef: ze wegen een pak suiker.
Ze vinden dat de fabrikant ongelijk heeft als dit pak suiker minder dan 998 gram weegt. Dit is het beslissingsvoorschrift.
De mogelijkheid dat dit pak toevalligerwijs minder dan 998 gram weegt, terwijl toch de fabrikant gelijk heeft, heet een fout van de eerste soort. De kans op zo'n fout heet het significantieniveau van de toets.
Ga na, dat die kans is: α = P(G < 998 | μ = 1002 en σ = 3) ≈ 0,091.
Meestal wordt geprobeerd om α kleiner te krijgen, want de consumentenbond doet niet graag foute uitspraken. Ze stellen dan voorafgaande aan de toets vast welke waarde van α nog acceptabel is en bepalen dan het bijbehorende beslissingsvoorschrift.
En natuurlijk nemen ze een grotere steekproef. Maar dan geldt wel de $\sqrt{n}$-wet...

‡

Opgaven

1. In de Uitleg zie je hoe de consumentenbond het gewicht van kilopakken suiker controleert.
   1. Er is hier sprake van een enkelzijdige normale toets. Kun je die naam verklaren?
   2. Waarom voert de consumentenbond een enkelzijdige toets uit? Hoe zou dat met de fabrikant zelf zijn?
   3. Wat moet de conclusie zijn als de consumentenbond vooraf een significantieniveau van 5% wilde hanteren?
   4. Bij welk gewicht zou er dan sprake zijn van een significant verschil?


2. Gebruik de gegevens in de Uitleg. Nu neemt de consumentenbond een steekproef van 100 pakken.
   1. Wat betekent dit voor de toets?
   2. Als in die steekproef het gemiddelde gewicht 998 gram zou zijn, zou de consumentenbond dan met een betrouwbaarheid van 95% gelijk krijgen?

Theorie

Iemand beweert: stochast X is normaal verdeeld met μ(X) = μ en σ(X) = σ.
Iemand anders vertrouwt het gemiddelde niet en vermoedt (bijvoorbeeld): μ(X) ≠ μ.
Dit wordt getoetst met een steekproef van grootte n. Je bepaalt dan het gemiddelde in de steekproef en kijkt of de afwijking van μ significant is.

Bij zo'n normale toets van het gemiddelde is de nulhypothese H₀: μ(X) = μ.
Daarnaast staat een alternatieve hypothese H₁: μ(X) ≠ μ.

Het gemiddelde $\overline{X}$ in de steekproef is ook normaal verdeeld met μ($\overline{X}$) = $\frac{n\cdot \mu }{n}$  = μ  en
σ($\overline{X}$) = $\frac{\sqrt{n}\cdot \sigma }{n}=\frac{\sigma }{\sqrt{n}}$ als de nulhypothese inderdaad waar is.
Bij de alternatieve hypothese hoort een kritiek gebied dat aangeeft waar de afwijking van μ zo groot is dat je de nulhypothese verwerpt. Dat kritieke gebied bepaal je op grond van een vooraf vastgesteld significantieniveau α, bijvoorbeeld:

P($\overline{X}$ < g₁ ∨ $\overline{X}$ > g₂ | μ($\overline{X}$) = μ en σ($\overline{X}$) = $\frac{\sigma }{\sqrt{n}}$) ≤ α

Hierin zijn g₁ en g₂ de grenswaarden van het kritieke gebied $\overline{X}$ < g₁ of $\overline{X}$ > g₂.
Het significantieniveau kies je voordat je de toets uitvoert, bijvoorbeeld 10%, 5% of 1%. De keuze geeft informatie over de significantie van de toets.

‡

Voorbeeld 1

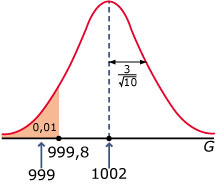
Volgens de fabrikant is het gewicht G (in gram) van zijn pakken suiker normaal verdeeld met μ(G) = 1002 en σ(G) = 3.
Omdat de consumentenbond veel klachten heeft binnengekregen waarin wordt gemeld dat de pakken suiker van deze fabrikant te weinig suiker bevatten, wordt er door hen getwijfeld aan dit gemiddelde. De consumentenbond stelt dat μ(G) < 1002.
In een steekproef van 10 is het gemiddelde 999 gram. Is dit bij een significantieniveau van 1% voldoende reden om aan te nemen dat de fabrikant ongelijk heeft?

Antwoord

• H₀: μ($\overline{G}$) = 1002 en σ($\overline{G}$) = $\frac{3}{\sqrt{10}}$ ≈ 0,95.
• H₁: μ($\overline{G}$) ≤ 1002.

Het significantieniveau is α = 0,01.

P($\overline{G}$ ≤ g | μ = 1002 en σ ≈ 0,95) = 0,01 geeft: g ≈ 999,8.
Het kritieke gebied wordt daarom: $\overline{G}$ ≤ 999,8.
Het in de steekproef gevonden gemiddelde geeft daarom inderdaad aanleiding om de bewering van de fabrikant in twijfel te trekken bij een significantieniveau van 1%.

‡

Voorbeeld 2

Volgens de fabrikant is zijn vulmachine zo ingesteld dat het gewicht G (in gram) van zijn pakken suiker normaal verdeeld is met μ(G) = 1002 en σ(G) = 3.
De fabrikant test zijn vulmachine door van een steekproef van 10 pakken het gemiddelde gewicht te berekenen. Hij doet uiteraard een dubbelzijdige toets.
Wat is het beslissingsvoorschrift bij een significantieniveau van 1%?

Antwoord

• H₀: μ($\overline{G}$) = 1002 en σ($\overline{G}$) = $\frac{3}{\sqrt{10}}$ ≈ 0,95.
• H₁: μ($\overline{G}$) ≠ 1002.

Het significantieniveau is α = 0,01.

P($\overline{G}$ ≤ g₁ of $\overline{G}$ ≥ g₂ | μ = 1002 en σ ≈ 0,95) = 0,01 geeft: g₁ ≈ 999,5 en g₂ ≈ 1004,5.
Het kritieke gebied wordt daarom: $\overline{G}$ ≤ 999,5 of $\overline{G}$ ≥ 1004,5.

‡

Opgaven

3. Je ziet in Voorbeeld 1 hoe de consumentenbond met een steekproef van 10 pakken het gewicht van kilopakken suiker controleert.
   1. Voer de beschreven toets zelf uit.
   2. Voer de toets nog eens uit, maar nu met een betrouwbaarheid van 99,5%. Is er nog steeds sprake van een significante afwijking?
   3. In plaats van een steekproef van 10 pakken wordt een steekproef van 50 pakken suiker genomen. Bij welke gewichten krijgt de consumentenbond nu met 99% betrouwbaarheid gelijk?


4. In Voorbeeld 2 zie je hoe je bij een tweezijdige toets te werk kunt gaan.
   1. Waarom is dit een tweezijdige toets? Wat gebeurt er met de onbetrouwbaarheidsdrempel `alpha`?
   2. Voer de beschreven toets zelf uit, maar nu met een significantieniveau van 5%.


5. In een fabriek heeft men het vermoeden dat het koolstofgehalte van een bepaalde staalsoort groter is dan 0,200%. Uit een steekproef van 80 metingen wordt een gemiddelde gevonden van 0,213%.
   De standaardafwijking van het koolstofgehalte is bekend en bedraagt `alpha = 0,041`%.
   1. Formuleer een geschikte nulhypothese en een alternatieve hypothese.
   2. Toets de hypothese met een onbetrouwbaarheidsdrempel van 0,01. Wat is je conclusie?


6. In een medisch laboratorium worden voortdurend cholesterolgehaltes in bloedmonsters bepaald. De gebruikte apperatuur wordt elk uur gecontroleerd met behulp van een ijkmonster. Hiervan is bekend dat het gemiddelde 175 mg per 100 mL zou moeten zijn. De controlemetingen aan het ijkmonster leveren op: 168, 170, 188, 170, 174, 190, 188, 171.
   Is er met een significantie van `alpha = 0,01` reden om aan te nemen dat de meetapperatuur niet goed meer werkt?
   

Verwerken

7. Een firma die batterijen levert voor rekenmachines, beweert dat die batterijtjes geschikt zijn om gemiddeld zo’n apparaat 3600 uur te laten werken. Ze gaan er van uit dat die levensduur normaal is verdeeld met een standaarddeviatie van 600 uur.
   In een aselect gekozen groep van 60 rekenmachines stop je de batterijen van deze firma. De gemiddelde levensduur blijkt 3300 uur te zijn. Kun je op grond van dit resultaat met een betrouwbaarheid van 97% de bewering van de firma verwerpen?
   


8. Volgens een wetenschappelijk tijdschrift is het gewicht van zeventienjarigen normaal verdeeld met een gemiddelde van 54,2 kg en een standaarddeviatie van 4,7 kg. Om deze bewering te toetsen wordt van 200 aselect gekozen zeventienjarigen het gewicht bepaald.
   1. Als het gemiddelde gewicht in de steekproef 53,3 kg is, heeft het tijdschrift dan met een significantie van 2,5% gelijk?
   2. Bij welk significantieniveau verwerp je de mening van het tijdschrift?
   3. Bij welk significantieniveau had je de mening van het tijdschrift verworpen als je in een veel kleinere steekproef van 10 zeventienjarigen hetzelfde gemiddelde gewicht had aangetroffen? Kun je een verklaring geven voor het verschil met het antwoord bij c?


9. Vacuüm verpakte vleeswaren mogen maximaal 0,022% natriumnitriet bevatten. Bij de keuringsdienst van waren controleren ze dit percentage.
   1. Formuleer de hypothese die getoetst wordt. Je mag aannemen dat het natriumnitrietpercentage normaal verdeeld is.
   2. Is de toets eenzijdig of tweezijdig? Formuleer ook de alternatieve hypothese.
   Bij de nulhypothese zijn er nog meer mogelijkheden voor `mu`. Omdat zelfs 0,022 toegestaan is, wordt er uitgegaan van `text(H)_0: mu = 0,022`. Hieronder zie je 25 meetresultaten:
   
   

   0,0219	0,0226	0,0225	0,0225	0,0216
   0,0219	0,0220	0,0216	0,0229	0,0226
   0,0214	0,0219	0,0226	0,0220	0,0212
   0,0225	0,0223	0,0215	0,0221	0,0223
   0,0224	0,0215	0,0228	0,0223	0,0223

   
   
   3. Toets met behulp van deze steekproef of er reden is tot bezorgdheid. Neem een significantieniveau van 5%.



percentage	freq.
3,445 –< 3,455	1
3,455 –< 3,465	0
3,465 –< 3,475	4
3,475 –< 3,485	3
3,485 –< 3,495	3
3,495 –< 3,505	4
3,505 –< 3,515	2
3,515 –< 3,525	2
3,525 –< 3,535	1

10. Op een pak melk staat: "Het natuurlijk vetgehalte van melk - zoals die van de koe komt - varieert van 3,7% tot 4,3%".
    Volle melk wordt in de fabriek altijd afgeroomd tot 3,5%. Een consumentenorganisatie besluit na te gaan of volle melk 3,5% vet bevat. In een aselecte steekproef van 20 pakken volle melk vindt ze de percentages die je in de tabel ziet.
    Men veronderstelt dat het vetgehalte van pakken melk normaal verdeeld is.
    1. Onderzoek met normaal waarschijnlijkheidspapier of de resultaten van deze proef reden geven om deze veronderstelling in twijfel te trekken.
    2. Schat met behulp van deze steekproef de parameter `sigma` van de normale verdeling.
    3. Toets met significantieniveau 0,05 of de consumentenorganisatie op grond van de steekproef de bewering op het pak kan verwerpen.

Testen

11. In een melkfabriek worden flessen machinaal gevuld. De gedoseerde hoeveelheid per fles is normaal verdeeld. Bij juiste instelling is de verwachte hoeveelheid 250 g per fles. Een kwaliteitsinspecteur neemt een steekproef van 9 flessen en vindt voor het gemiddelde 252 g. De standaardafwijking is 2 g.
    Toets, met significantieniveau `alpha = 0,05`, `text(H)_0: mu = 250` g tegen `text(H)_1: mu != 250` g.
    


12. Een partij kobaltchloride wordt bij levering door de ontvanger gekeurd op het gehalte kobalt. Volgens de leverancier is het gehalte 16,4%. Hieronder zie je de resultaten van de metingen.
    
    

    16,2	15,8	16,1	15,8	15,9
    15,9	16,2	16,1	16,2	16,0
    15,8	15,9	16,1	15,8	16,0
    16,0	16,0	15,9	16,2	16,2
    16,0	16,1	16,0	15,9	16,3

    
    
    Toets met behulp van deze resultaten of de leverancier gelijk heeft. Je mag aannemen dat het gehalte kobalt normaal verdeeld is. Neem als significantieniveau 0,02.