Binomiale toetsen

Inleiding

Meestal ga je er van uit dat bij het verwekken van kind de kans op een jongen even groot is als die op een meisje: de kans op een meisje is 50% is je nulhypothese. Als bij een zekere Nederlandse gemeente in een bepaald jaar 60% van de geboren kinderen een meisje is dan denk je niet meteen dat de kans op een meisje nu wel 60% moet zijn geworden, maar je vraagt je wel af of de kans op een meisje in Nederland soms meer dan 50% is geworden. Zo'n hypothese kun je heel goed toetsen bijvoorbeeld door te kijken naar de geboren kinderen van het volgende jaar. Maar wanneer zeg je nu dat de kans op een meisje niet langer 50% is?

Je leert nu:

hypothesen toetsen met behulp van de binomiale kansverdeling;
het begrip significantieniveau;
bij een gegeven significantieniveau een binomiale toets uitvoeren.

Je kunt al:

werken met binomiale kansverdelingen;
de begrippen nulhypothese, alternatieve hypothese en kritiek gebied.

Verkennen

> Wat is de nulhypothese en wat de alternatieve hypothese in dit geval?
> Stel je voor dat er in je steekproef 348 meisjes voorkomen. Hoe groot is nu de kans dat de nulhypothese ten onrechte wordt verworpen?
> Stel je eens voor dat je de kans dat de nulhypothese ten onrechte wordt verworpen maximaal 1% wilt hebben. Wat wordt dan het kritieke gebied van de toets?

Uitleg

In 2006 was in de Nederlandse gemeente A 60% van de geboren kinderen een meisje. Je vraagt je af of de kans op een meisje in Nederland soms meer dan 50% is geworden. Je neemt in 2007 een steekproef van 650 in dat jaar geborenen door heel Nederland en vraagt of het een jongen dan wel een meisje betreft.
Je wilt nu vooraf vaststellen bij welk aantal meisjes M in deze steekproef je kunt zeggen dat de kans op een meisje inderdaad meer dan 50% is. M is een binomiale stochast.

Je toetst H₀: p = 0,5 tegen H₁: p > 0,5.
Je gebruikt een steekproef van grootte n = 650.

Bij zo'n toets neem je als uitgangspunt het vermijden van een fout van de eerste soort: de kans dat je H₀ ten onrechte verwerpt moet kleiner zijn dan (bijvoorbeeld) 5%. Deze 5% heet het significantieniveau of de onbetrouwbaarheidsdrempel van de toets en wordt aangegeven met α. Je spreekt dus vooraf af dat (bijvoorbeeld) α = 0,05.

Je kritieke gebied is M > g dan moet:
P(H₀ verwerpen | H₀ is waar) = P(M > g | p = 0,5 en n = 650) ≤ 0,05.
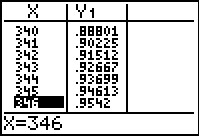
Dus moet P(M ≤ g | p = 0,5 en n = 650) > 0,95.
Je grafische rekenmachine geeft: g = 346.

Als je dus meer dan 346 meisjes in je steekproef aantreft mag je met een significantieniveau van 5% besluiten dat de kans op een meisje meer dan 50% is.

‡

Opgaven

In de Uitleg gaat het weer om de hypothese dat de kans op de geboorte van een meisje 50% is. Het siginificantieniveau van de toets is 5%.
1. Leg uit wat dit significantieniveau precies betekent.
2. Er is hier sprake van een enkelzijdig binomiale toets. Kun je die naam verklaren?
3. Reken zelf het kritieke gebied van deze toets na.
4. Waarom kun je ook zeggen dat de beschreven toets een betrouwbaarheid heeft van 95%?

Bekijk nog eens de toets in de Uitleg.
1. Voer deze toets nog eens uit, maar nu met een significantieniveau van 1%.
2. Welke invloed heeft het verkleinen van het significantieniveau op het kritieke gebied?
3. Waarom wordt het significantieniveau niet nog veel kleiner genomen, zeg 0,1%?

Theorie

Stel je voor dat voor een binomiale stochast X de gangbare opvatting is dat p = p₀ de kans is dat een element van de steekproef een bepaalde eigenschap heeft. Iemand bestrijdt deze opvatting en beweert dat p > p₀.

Je toetst H₀: p = p₀ tegen H₁: p > p₀ met behulp van een steekproef van grootte N.

Het kritieke gebied (de waarden in de steekproef waarbij je H₀ verwerpt) van de toets stel je vast door te eisen dat de kans dat je H₀ verwerpt terwijl hij toch waar is kleiner blijft dan een bepaalde waarde die je vooraf kiest. Die waarde noem je het significantieniveau of de onbetrouwbaarheidsdrempel van de toets en hij wordt aangegeven met α. Je spreekt dus vooraf af dat (bijvoorbeeld) α = 0,05. Dit betekent:
P(H₀ verwerpen | H₀ is waar) = P(X > g | p = p₀ en n = N) ≤ 0,05.
Op grond hiervan bereken je g en zo stel je het kritieke gebied van de toets vast.

Dit is een rechtszijdige toets omdat H₁: p > p₀.
Zo bestaat er ook een linkszijdige toets met H₁: p < p₀.
En een tweezijdige toets met H₁: p ≠ p₀.
In dit laatste geval trek je aan beide zijden van het op grond van H₀ verwachte aantal in de steekproef een grens. De onbetrouwbaarheidsdrempel α verdeel je dan in twee gelijke delen voor elk deel van het kritieke gebied.

‡

Voorbeeld 1

Voor een bepaalde toets scoort gemiddeld 72% van de kandidaten een voldoende. Deze keer hebben 16 van de 30 kandidaten een voldoende gehaald, duidelijk minder dan 72%. Wijkt dit resultaat significant af van het verwachte resultaat als je een siginificantieniveau van 10% hanteert?

Antwoord

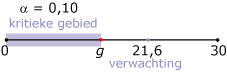Je kunt deze vraag "vertalen" naar een linkszijdige binomiale toets:

H₀: p = 0,72
H₁: p < 0,72

met een steekproefgrootte van 30 en stochast X is het aantal kandidaten met een voldoende in deze steekproef. Het significantieniveau is α = 0,10.

Je bepaalt het kritieke gebied uit: P(X ≤ g | p = 0,72 en n = 30) ≤ 0,10.
Dit levert op: g = 17 en dus wordt het kritieke gebied X ≤ 17.

Het resultaat van 16 voldoendes ligt binnen het kritieke gebied, dus inderdaad wijkt het resultaat significant af van het verwachte resultaat.

‡

Voorbeeld 2

Om te bepalen of een dobbelsteen eerlijk is, kun je bijvoorbeeld 50 keer met deze dobbelsteen werpen en het aantal keren "zes ogen" tellen. Bij hoeveel keer "zes ogen" mag je dan besluiten dat hij niet eerlijk is? Neem een significantieniveau van 1%.

Antwoord

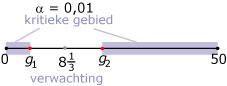Je kunt deze vraag "vertalen" naar een tweezijdige binomiale toets:

H₀: p = $\frac{1}{6}$
H₁: p ≠ $\frac{1}{6}$

met een steekproefgrootte van 50 en stochast X is het aantal keren "zes ogen" in deze steekproef. Het significantieniveau is α = 0,01.

Nu moet P(X ≤ g₁ ∨ X > g₂ | p = $\frac{1}{6}$ en n = 50) ≤ 0,01.
Je bepaalt de twee grenzen daarom uit:

P(X ≤ g₁ | p = $\frac{1}{6}$ ∧ n = 50) ≤ 0,005
P(X > g₂ | p = $\frac{1}{6}$ en n = 50) ≤ 0,005

Ga na, dat het kritieke gebied wordt: X ≤ 1 of X ≥ 16.
Bij deze aantallen zessen mag je aannemen dat de dobbelsteen niet eerlijk is.

‡

Voorbeeld 3

Voor een bepaalde toets scoort gemiddeld 72% van de kandidaten een voldoende. Deze keer hebben 16 van de 30 kandidaten een voldoende gehaald, duidelijk minder dan 72%. Wijkt dit resultaat siginficant af van het verwachte resultaat als je een siginificantiniveau van 10% hanteert?

Antwoord

Dit is hetzelfde probleem als in voorbeeld 1. Je kunt het echter ook op een andere manier oplossen. Daarbij maak je meteen gebruik van het testresultaat: 16 van de 30 kandidaten haalden een voldoende.

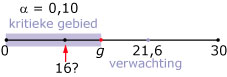
Als 16 in het kritieke gebied van de toets ligt, dan moet dit gebied minstens X ≤ 16 zijn (wellicht groter). En dan moet
P(X ≤ 16 | p = 0,72 en n = 30) ≤ 0,10.
Deze overschrijdingskans is 0,0225 en dus inderdaad kleiner dan α = 0,10.

Je weet nu zeker dat 16 in het kritieke gebied van de toets ligt, ook al heb je de grens ervan niet vastgesteld. De nulhypothese wordt verworpen, het resultaat wijkt significant af.

‡

Opgaven

Bestudeer Voorbeeld 1.
1. Voer de beschreven toets zelf uit.
2. Voer de toets nog eens uit, maar nu met een betrouwbaarheid van 95%. Is er nog steeds sprake van een significante afwijking?

In Voorbeeld 2 zie je hoe je bij een tweezijdige toets te werk kunt gaan.
1. Waarom is dit een tweezijdige toets? Wat gebeurt er met de onbetrouwbaarheidsdrempel `alpha`?
2. Voer de beschreven toets zelf uit, maar nu met een significantieniveau van 5%.

In Voorbeeld 3 wordt de toets in voorbeeld 1 opnieuw bekeken.
1. Waarom is het in dit geval niet nodig om het kritieke gebied vast te stellen?
2. Wat betekent het als de overschrijdingskans kleiner is dan de onbetrouwbaarheidsdrempel?
3. Wat betekent het als de overschrijdingskans groter is dan de onbetrouwbaarheidsdrempel?

Je toetst `text(H)_0: p = 0,35` tegen `text(H)_1: p > 0,35` met een significantieniveau van 5%.
1. Bepaal het kritieke gebied bij een steekproef met grootte 100.
2. Doe hetzelfde bij een steekproef van grootte 1000.
3. En nog eens bij een steekproef met grootte 10.000.
4. Welke invloed heeft de grootte van de steekproef op de grens van het kritieke gebied? Wat heeft dit te maken met de standaardafwijking van de gebruikte binomiale verdeling?
5. Waarom neemt men niet altijd een zo groot mogelijke steekproef?

Je toetst `text(H)_0: p = 0,75` tegen `text(H)_1: p != 0,75` met een onbetrouwbaarheidsdrempel van `alpha = 0,05`.
1. Bepaal het kritieke gebied als je een representatieve steekproef van 100 gebruikt.
2. Stel je voor dat je vooraf hebt bepaald dat in de steekproef 80 elementen de betreffende eigenschap hebben. Leg uit waarom in dat geval het berekenen van het kritieke gebied niet nodig is. Laat zien hoe je in zo’n geval sneller te werk kunt gaan.

Verwerken

Op een grote school slaagt elk jaar ongeveer 96% van de eindexamenkandidaten. Het afgelopen jaar viel het resultaat behoorlijk tegen. Slechts 92 van de 107 kandidaten haalden het eindexamen. Op andere scholen in de buurt waren er geen grote veranderingen ten opzichte van de slagingspercentages van de voorafgaande jaren. Er wordt geroepen: "De kwaliteit van de school holt achteruit". Een van de geslaagden is het daarmee niet eens: "Nee hoor; dat is helemaal niet waar. Dat kan gewoon eens een jaar voorkomen. Die kans bestaat nou eenmaal".
1. De uitspraak van deze geslaagde kun je toetsen. Hoe luiden de nulhypothese en de alternatieve hypothese?
2. Bereken de kans op 92 of minder geslaagden als de nulhypothese waar is.
3. Krijgt de geslaagde leerling gelijk als het significantieniveau 0,01 is?

Het hoofd van de personeelsadministratie van een groot bedrijf heeft het idee dat het ziekteverzuim op maandag veel groter is dan op de andere dagen in de week. Om dit te onderzoeken vraagt hij het aantal ziekteverzuimdagen per werkdag op in een bepaalde maand. In deze tabel zie je de resultaten.

dag ma di wo do vr

aantal zieken 95 61 58 63 11
1. Hoeveel zieken zou je op maandag mogen verwachten als het ziekteverzuim onafhankelijk is van de weekdag?
Het vermoeden van de bedrijfsleider kun je met deze gegevens toetsen. Als nulhypothese kun je nemen: `text(H)_0: p = 0,2`.
1. Formuleer de alternatieve hypothese.
2. Krijgt de bedrijfsleider gelijk? Neem een significantieniveau van `alpha = 0,05`.

Bij een loterij die elke week plaatsvindt, moet je op een formulier met daarop de getallen 1 tot en met 19, drie getallen aankruisen. Nadat de inlevertijd is verstreken, worden aselect drie getallen getrokken. Een deelnemer die op zijn lot tenminste twee van de drie getrokken getallen heeft aangekruist, krijgt een prijs.
1. Toon aan dat, afgerond op twee decimalen, de kans op een prijs gelijk is aan 0,05.
Iemand beweert dat zijn kans op een prijs groter is dan 0,05. Deze bewering wordt getoetst door gedurende honderd weken het aantal prijzen van deze persoon te noteren. Er wordt een significantieniveau van 1% gekozen.
1. Hoeveel prijzen moet deze persoon in die honderd weken tenminste hebben gewonnen om hem gelijk te kunnen geven?

Iemand wil de zuiverheid van een geldstuk controleren en besluit er 500 keer mee te werpen.
Bij welke aantallen "kop" zal hij besluiten dat het geldstuk onzuiver is als hij een betrouwbaarheid van 90% hanteert?

In 1998 zijn er in Nederland 179.568 baby’s geboren. 90.096 meisjes en 89.472 jongens. Met deze getallen kun je toetsen of de kans op een meisje gelijk is aan de kans op een jongen.
De nulhypothese is dan weer: de kans op een meisje is 0,5.
1. Neem aan dat het aantal meisjes binomiaal is verdeeld. Welke parameters heeft deze verdeling?
2. Moet de nulhypotese verworpen of geaccepteerd worden als de onbetrouwbaarheidsdrempel 5% is?
3. En als de toets een betrouwbaarheid van 99% moet hebben?

Testen

Op het instituut voor toepast psychologisch onderzoek onderzoekt men helderziendheid. Mensen die beweren helderziend te zijn, worden uitgenodigd voor het volgende experiment. De helderziende wordt opgesloten in een kamer. Hij krijgt een serie van drie zeer verschillende plaatjes. Op hetzelfde ogenblik ontvangt een ander persoon in dezelfde ruimte dezelfde drie plaatjes. Deze persoon krijgt de opdracht om zich vijf minuten lang op één van de drie plaatjes te concentreren. Na die vijf minuten moet de helderziende dan aangeven op welk plaatje de ander zich geconcentreerd heeft. De twee deelnemers kunnen elkaar niet zien. Ze hebben een koptelefoon op waardoor ze steeds een nieuwe opdracht krijgen. Dit proces wordt in totaal 40 keer herhaald met steeds nieuwe series plaatjes. De nulhypothese die men wil toetsen luidt: de helderziende is niet helderziend. Dat kan men toetsen met behulp van het aantal keren dat de helderziende hetzelfde plaatje aangeeft als de ander. Als de nulhypothese waar is dan is het aantal keren "hetzelfde plaatje" binomiaal verdeeld.
1. Welke parameters heeft deze binomiale verdeling?
2. Helderziende X geeft 17 keer het juiste plaatje aan. Bereken de kans dat dit gebeurt als de nulhypothese juist is.
3. Bereken de kans dat de nulhypothese ten onrechte verworpen wordt als er afgesproken wordt dat er sprake is van helderziendheid bij meer dan 20 juiste plaatjes.
4. Er wordt afgesproken dat het significantieniveau 0,05 is. Wordt helderziende Y helderziend verklaard als hij 18 plaatjes goed heeft?

Een kweker wil onderzoeken of zijn kruisingsmethode als resultaat heeft dat 25% van de bessenstruiken gevoelig is voor meeldauw. Hij constateert dat van de 100 bessenstruiken er 33 last hebben van meeldauw.
Mag hij nu met een significantieniveau van 5% aannemen dat toch maar 25% gevoelig is voor meeldauw?

dag	ma	di	wo	do	vr
aantal zieken	95	61	58	63	11