Standaardiseren

Inleiding

In het voorgaande heb je met de normaalkromme leren werken. Een normale kansverdeling wordt gekarakteriseerd door gemiddelde μ en standaardafwijking σ. Maar er zijn situaties denkbaar waarin je één van beide niet weet. Bijvoorbeeld als je bij het vullen van bijvoorbeeld een pak suiker het vulgewicht nauwkeuriger wilt afstellen.

Je leert nu:

• het begrip standaardnormale stochast;
• verwachtingswaarde of standaarddeviatie berekenen bij een normale stochast.

Je kunt al:

• werken met normale stochasten;
• kansen berekenen bij normale stochasten;
• grenswaarden terugzoeken bij normale kansen.

Verkennen

Het vulgewicht van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. Maar nu bevat ongeveer 25% van de pakken minder dan 1000 gram.

> Je wilt dat niet meer dan 5% van de pakken minder dan 1000 gram bevat. Hoe doe je dat?
> Stel dat je drie kilopakken suiker koopt. Hoe groot is de kans dat je bij de gegeven insteling minder dan 3000 gram suiker hebt?

Uitleg

Bekijk de applet op

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Statistiek en kansrekening > Continue kansmodellen > Standaardiseren > Uitleg

Het vulgewicht van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. Maar nu bevat ongeveer 25% van de pakken minder dan 1000 gram.
Je wilt dat niet meer dan 5% van de pakken minder dan 1000 gram bevat.
In de applet kun je dit bijvoorbeeld bewerkstelligen door het gemiddelde vulgewicht μ te verhogen. Maar daar zal de fabrikant niet blij van worden, dat is een dure oplossing.
Maar je kunt dit ook voor elkaar krijgen door de vulmachine nauwkeuriger te laten werken: je verkleint de standaardafwijking σ.

Met de applet kun je de aangepaste μ of σ wel vinden, maar hoe bereken je die?
Kennelijk gaat het daarbij om het verschuiven, dan wel lijnvermenigvuldigen van de grafiek.

Het vulgewicht van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. De kans dat een pak minder dan 1000 gram is ongeveer 25%.
Als je drie pakken suiker koopt doe je in feite drie keer hetzelfde kansexperiment.
Omdat het telkens een keuze uit een zeer grote hoeveelheid kilopakken suiker betreft, mag je dit opvatten als onafhankelijke trekkingen.
En dus geldt de $\sqrt{n}$-wet: het totale gewicht T is ook normaal verdeeld met een gemiddelde van 3 · μ = 3006 gram en een standaardafwijking van $\sqrt{3}$ · σ ≈ 5,3 gram.

De kans dat je nu minder dan 3000 gram hebt is kleiner dan 25% geworden:
P(T < 3000) ≈ 0,1243.

‡

Opgaven

1. Bestudeer de Uitleg. Werk met de daarin genoemde applet om de volgende vragen te beantwoorden.
   1. Pas eerst alleen het gemiddelde aan. Bij welk gemiddelde is niet meer dan 5% van de pakken lichter dan 1000 gram?
   2. Waarom is dit voor de fabrikant een dure oplossing?
   3. Laat nu het gemiddelde staan op 1002 gram en pas de standaardafwijking aan. Bij welke standaardafwijking is niet meer dan 5% van de pakken te licht?
   4. Welke mogelijke voor- en nadelen heeft deze oplossing voor de fabrikant?
   5. Bestudeer in de Uitleg de trekking van een steekproef van drie pakken suiker. Bereken zelf de kans dat je meer dan 3010 gram hebt in totaal.


2. Aan een examen hebben 200 kandidaten meegedaan. Het examen bestaat uit twee gedeelten: een schoolexamen (SE) en een centraal examen (CE). Uit onderzoek is gebleken dat de examencijfers normaal verdeeld zijn. Het gemiddelde cijfer voor het schoolexamen was een 6,5 en de standaardafwijking was 1,0. Het gemiddelde cijfer voor het centraal examen was een 5,5 en de standaardafwijking was 2,0. Een leerling heeft een 7,0 gehaald voor het schoolexamen en een 6,0 voor het centraal examen.
   1. Noem het cijfer voor het schoolexamen `S` en dat voor het centraal examen `C`. Schets de normaalkrommen van de verdeling van zowel `S` als `C`. Geef de cijfers van de leerling in die figuren aan.
   2. Kun je de prestaties van de leerling voor het SE en het CE nu goed met elkaar vergelijken? Licht je antwoord toe.
   3. Je kunt beter in beide gevallen kijken naar de afwijking van het gemiddelde, dus naar `S_2 = S - mu(S)` en `C_2 = C - mu(C)`. Schets de beide normaalkromme van `S_2` en `C_2` en geef de resultaten van de leerling erin aan. Wat is het gemiddelde van beide normale verdelingen?
   4. Gaat nu het vergelijken van de twee cijfers van de leerling beter?
   5. Je kunt beide verdelingen nog beter op elkaar afstemmen door te zorgen dat ze even "breed" zijn. Dat doe je door de normaalkrommen van `S_3 = (S - mu(S))/(sigma(S))` en `C_3 = (C - mu(C))/(sigma(C))` te tekenen en daar de resultaten van de leerling in te zetten. Maak deze figuren en leg uit voor welk onderdeel de leerling het best heeft gepresteerd.

Theorie

De vorm van de normaalkromme hangt af van het gemiddelde μ en de standaarddeviatie σ. Neem je μ = 0 en σ=1, dan krijg je de standaard normaalkromme.
Elke normaalkromme kan ontstaan uit de standaard normaalkromme: `Z = (x - mu)/(sigma)`.

Er is daarom een standaard normale stochast Z die kan worden gebruikt om kansen te bepalen bij elke willekeurige normale stochast X en er geldt: `text(P)(X <= x) = text(P)(Z <= (x - mu)/(sigma))`.
Je noemt dit het standaardiseren van de normale stochast X.

Heb je de som S van n gelijke normale stochasten X, dan geldt de `sqrt(n)`-wet:
S is normaal verdeeld met μ(S) = n · μ(X) en σ(S) = `sqrt(n)` · σ(X).

‡

Voorbeeld 1

Het vulgewicht G van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. Maar nu bevat ongeveer 25% van de pakken minder dan 1000 gram.
Je wilt dat niet meer dan 5% van de pakken minder dan 1000 gram bevat.
Hoeveel moet je daartoe het gemiddelde vulgewicht μ verhogen?

Antwoord

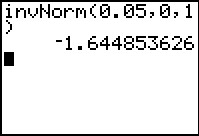
Je wilt oplossen: P(G < 1000 | μ = m en σ = 3) = 0,05.
Na standaardiseren vind je P(Z < $\frac{1000-m}{3}$) = 0,05.
De GR geeft z = $\frac{1000-m}{3}$ ≈ –1,64.
Je vindt dan m ≈ 1004,9 gram voor het nieuwe gemiddelde.

‡

Voorbeeld 2

Het vulgewicht G van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. Maar nu bevat ongeveer 25% van de pakken minder dan 1000 gram.
Je wilt dat niet meer dan 5% van de pakken minder dan 1000 gram bevat.
Hoe moet je daartoe de standaardafwijking σ aanpassen?

Antwoord

Je wilt oplossen: P(G < 1000 | μ = 1002 en σ = s) = 0,05.
Na standaardiseren vind je P(Z < $\frac{1000-1002}{s}$) = 0,05.
De GR geeft z = $\frac{1000-1002}{s}$ ≈ –1,64.
Je vindt dan s ≈ 1,2 gram voor de nieuwe standaardafwijking.

‡

Voorbeeld 3

Het vulgewicht X van kilopakken suiker is ingesteld op een gemiddelde van μ = 1002 en een standaardafwijking van σ = 3 gram. De kans dat een pak minder dan 1000 gram suiker bevat is dan meer dan 25%.
Je koopt 5 van die kilopakken suiker. Hoe groot is de kans dat je minder dan 5000 gram suiker hebt?

Antwoord

Je voert nu 5 keer hetzelfde kansexperiment uit, namelijk het kiezen van een pak suiker uit een heel groot aantal van die pakken. Het totale gewicht T is daarom ook normaal verdeeld met μ(T) = 5 · μ(X) = 5010 en σ(T) = $\sqrt{5}$ · σ(X) ≈ 6,7 gram.

De gevraagde kans is: P(T < 5000 | μ = 5010 en σ ≈ 6,7) ≈ 0,0678.

‡

Opgaven

3. In Voorbeeld 1 zie je hoe je de standaardnormale verdeling toepast bij het berekenen van een gemiddelde.
   1. Reken zelf het gemiddelde nog eens na.
   2. Stel je voor dat de eisen worden aangescherpt: niet meer dat 2,5% van de pakken suiker mag minder dan 1000 gram wegen. Welk gemiddeld vulgewicht moet je dan hanteren?
   3. Is het mogelijk om te eisen dat 0% van de pakken te licht is? Verklaar je antwoord.


4. Van een bepaald type batterij is de levensduur normaal verdeeld met een gemiddelde van 80 uur en een standaardafwijking van 255 minuten.
   1. De fabrikant vermeldt op de verpakking dat deze batterijen 75 uur mee gaan. Hoeveel procent van de batterijen haalt deze levensduur niet?
   2. Door het verbeteren van het fabricageproces gaan de batterijen gemiddeld langer mee. De standaardafwijking van de levensduur blijft hetzelfde. De fabrikant garandeert nu dat slechts 1% van de batterijen geen 90 uur mee gaat. Hoeveel bedraagt nu de gemiddelde levensduur van dit soort batterijen?



5. In Voorbeeld 2 zie je hoe je de standaardnormale verdeling toepast bij het berekenen van een standaardafwijking.
   1. Reken zelf de standaardafwijking nog eens na.
   2. Stel je voor dat de eisen worden aangescherpt: niet meer dat 2,5% van de pakken suiker mag minder dan 1000 gram wegen. Welke standaarddeviatie moet je dan hanteren?


6. Aan een examen nemen 3000 kandidaten deel. De resultaten zijn normaal verdeeld. Het gemiddelde cijfer is 5,0. Slechts 10% van de kandidaten haalden een 7,0 of hoger.
   Welke standaardafwijking heeft de verdeling van deze cijfers? Geef je antwoord in één decimaal nauwkeurig.
   


7. Als je een steekproef van `n` pakken suiker trekt uit de (veel grotere) dagproductie van pakken suiker, moet je met de `sqrt(n)`-wet rekening houden. Zie Voorbeeld 3.
   Voor de dagproductie geldt dat het gemiddelde gewicht van een pak suiker 1002 gram is met een standaardafwijking van 3 gram. Je trekt een steekproef van 10 pakken suiker uit die dagproductie.
   1. Welk gemiddelde gewicht zal de totale hoeveelheid suiker in die steekproef hebben? En welke standaarddeviatie hoort daar bij?
   2. Bereken de kans dat het totale gewicht in de steekproef meer is dan 10 kg.
   3. Welk gemiddelde gewicht zal één pak suiker in die steekproef hebben? En welke standaarddeviatie hoort daar bij?
   4. Bereken de kans dat het gemiddelde gewicht van één pak in de steekproef meer is dan 1 kg.


8. Kerrie is te krijgen in zakjes van 150 g. De zakjes worden in de fabriek machinaal gevuld. Bekend is dat de gewichten van de zakjes normaal verdeeld zijn. De vulmachine is zo afgesteld dat het gemiddelde gewicht 155 g wordt met een standaardafwijking van 6 g.
   1. Ter controle worden 100 zakjes uit de dagproductie genomen en gewogen. Tussen welke gewichtsgrenzen zal 95% van de zakjes uit de steekproef liggen?
   2. Hoe groot is de steekproef als minder dan 5% van de zakjes uit die steekproef lichter is dan 154 gram?

Verwerken

9. Een fabrikant vindt dat 5% van al zijn kilopakken suiker te licht mag zijn.
   1. Welk gemiddeld vulgewicht moet je nu instellen bij een gegeven standaarddeviatie van 4 gram (de nauwkeurigheid van de vulmachine)?
   2. De Europese Unie stelt een scherpere eis: slechts 2% van de pakken mag te licht zijn. Welk gemiddelde vulgewicht moet de fabrikant nu instellen?
   De fabrikant wordt niet blij van het verhogen van het gemiddelde vulgewicht, want dat kost hem nogal wat extra geld. Hij moet dan immers gemiddeld meer suiker in een pak stoppen. Daarom besluit hij om niet het gemiddelde vulgewicht aan te passen, maar de vulmachine nauwkeuriger af te stellen. Het gemiddelde vulgewicht is 1003 gram en hij gaat uit van de eis van de EU dat 2,5% van de pakken te licht mag zijn.
   3. Welke standaardafwijking mag zijn vulmachine nu veroorzaken?


10. Bij de serieproductie van een bepaald type auto wordt het plaatsen van het stuur door mensen gedaan. Deze handeling kost gemiddeld 55 seconden. De handelingstijd `T` blijkt ongeveer normaal te zijn verdeeld rond dit gemiddelde met een standaard afwijking van 4 seconden.
    1. Er worden in een bepaalde maand 1200 van deze auto’s geproduceerd. Schat het aantal auto’s waarbij het langer dan 60 seconden geduurd heeft om het stuur te plaatsen.
    2. Hoeveel tijd hebben de 5% snelste handelingstijden gekost?
    3. De fabrikant van deze auto’s onderzoekt of een machine de mens kan vervangen. De gemiddelde afhandelingstijd is ook dan 55 seconden, maar de standaardafwijking wordt veel kleiner. Nu duurt maar 1% van alle afhandelingstijden meer dan 60 seconden. Welke standaarddeviatie geldt voor deze machine?


11. In een fabriek worden schroeven gemaakt met verschillende afmetingen. In opdracht moet er een partij schroeven gemaakt worden waarvan de kop een diameter heeft tussen de 9,98 mm en 10,03 mm. Schroeven met een te dikke of te dunne kop worden afgekeurd. De gemiddelde diameter is afhankelijk van de waarde waarop de machine is ingesteld. De fabrikant stelt de machine in op een diameter van 9,99 mm. De standaardafwijking van de machine bedraagt 0,02 mm.
    1. Hoeveel procent van de schroeven zal goedgekeurd worden?
    2. Hoeveel procent van de schroeven zal worden goedgekeurd als de fabrikant er in slaagt de standaardafwijking van de machine terug te brengen naar 0,01 mm?
    De fabrikant wil dat 99% van de schroeven goedgekeurd wordt. Hij denkt dat te kunnen bereiken door een andere instelwaarde van de machine te kiezen. Ook kan de machine fijner worden afgesteld, waardoor de standaardafwijking verandert.
    3. Bij welke afstellingen zal hem dat lukken?


12. Bij een veredelingsbedrijf van zaden wordt de lengte van een bepaalde plant gemeten. Men vindt dat de lengten van deze planten normaal verdeeld zijn. 12,5% van de planten heeft een lengte van meer dan 60 cm en 39% van de planten is niet groter dan 30 cm.
    1. Bereken de gemiddelde lengte en de standaardafwijking van deze plantensoort.
    Te kleine planten zijn niet geschikt voor de zaadontwikkeling. Deze planten worden vernietigd. Het blijkt dat 30% van de planten vernietigd moet worden.
    2. Tot welke lengte worden de planten vernietigd?


13. Een bakker bakt kerststollen van 1000 g.
    1. Wat is de standaardafwijking als het gemiddelde gewicht 1000 g is en 5% van de stollen minder weegt dan 900 g?
    2. Als de standaardafwijking van de stollen 60 g is, hoeveel procent van de stollen weegt dan minder dan 900 g?
    3. Hoe groot is het gemiddelde gewicht van de stollen bij een standaardafwijking van 65 g als 5% van de stollen minder weegt dan 900 g?
    Je koopt bij deze bakker drie kerststollen. Ga er van uit dat het gemiddelde gewicht 1000 g is met een standaardafwijking van 50 g.
    4. Hoe groot is de kans dat deze drie kerststollen samen minder dan 2950 gram wegen?
    5. Hoe groot is de kans dat het gemiddelde gewicht van deze drie kerststollen minder dan 960 gram is?


14. Limburgse kaas wordt verkocht in pakjes van 200 g. De snijmachine is zo afgesteld dat het gewicht van de pakjes normaal verdeeld is met een gemiddelde van 202,5 g en een standaardafwijking van 4,0 g.
    1. Hoe groot is de kans dat een pakje minder dan 200 g weegt?
    2. In een doos gaan 50 pakjes kaas. Hoe groot is de kans dat een doos minder dan 10 kg kaas bevat?
    3. Een winkelier bestelt voor een bepaalde week een groot aantal pakjes kaas. Minder dan 10% daarvan weegt meer dan 203 gram. Hoeveel pakjes kaas heeft hij besteld?

Testen

15. Van een partij suiker, verpakt in pakken van 1000 g, blijkt 15% minder te wegen dan 1000 g. Het vulgewicht is gelijk aan het gemiddeld gewicht.
    Als de standaardafwijking van de machine 7 g bedraagt, waar staat het vulgewicht dan op ingesteld?
    


16. Een machine die flessen vult, is ingesteld op een gemiddeld vulgewicht van 1015 g. De standaardafwijking is onbekend. Uit onderzoek is gebleken dat 1,5% van de flessen een gewicht heeft dat kleiner is dan 1000 g.
    Bepaal de standaardafwijking.
    


17. Bloemzaadjes worden verkocht in zakjes van 30 g. Het gewicht van een zakje uit een grote partij is normaal verdeeld met een gemiddelde van 31 g en een standaardafwijking van 0,6 g. Uit de partij wordt willekeurig een zakje genomen.
    1. Hoe groot is de kans dat het zakje meer dan 32 g weegt?
    2. Hoe groot is de kans dat het gewicht van het zakje meer dan 4% afwijkt van het gemiddelde?
    3. Hoeveel procent van de zakjes weegt te weinig?
    4. De fabrikant vindt het percentage bij c te groot en besluit het gemiddelde vulgewicht wat te verhogen tot maar 1% van de zakjes te licht is. Welk vulgewicht moet hij dan instellen?
    Uit de oorspronkelijke partij wordt een steekproef van 25 zakjes getrokken.
    1. Hoe groot is de kans dat de totale hoeveelheid bloemzaadjes meer dan 780 g weegt?
    2. Hoe groot is de kans dat het gemiddelde gewicht van een zakje uit de steekproef meer dan 4% afwijkt van het populatiegemiddelde?