Normale kansen

Inleiding

Bij heel veel continue toevalsvariabelen blijkt een mooie symmetrische klokvormige kansdichtheidsfunctie te horen. Dat geldt voor het gewicht van appels, de lengte van een grote groep mensen, vulgewichten van literpakken, e.d.
De beroemde wiskundige Gauss (1777 - 1855) vond er een formule voor. Sinds die tijd spreek je van een "Gausskromme" of ook wel "normaalkromme". Je zegt bijvoorbeeld dat het vulgewicht van pakken suiker normaal verdeeld is.

Je leert nu:

• kansen berekenen bij normaal verdeelde stochasten.

Je kunt al:

• werken met continue stochasten;
• de normaalkromme als voorbeeld van kansdichtheidsfunctie hanteren;
• de vuistregels voor de normaalkromme gebruiken.

Verkennen

Hier zie je de lengteverdeling van een groep soldaten op een bepaalde kazerne.

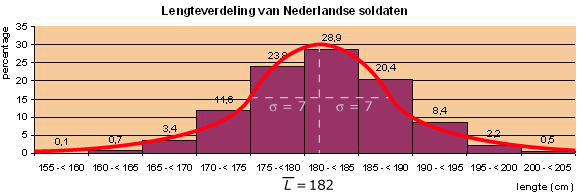
Bij de lengte L hoort een normaalkromme met gemiddelde μ(L) = 182 en standaardafwijking σ(L) = 7 cm.

> Wat stelt nu P(L < 175) voor?
> Waarom kun je deze kans uit de figuur gemakkelijk berekenen en P(L < 171) niet zo eenvoudig?
> Wat kun je zeggen van P(L = 175)?``

Uitleg

Bekijk de lengteverdeling van een groep soldaten op een bepaalde kazerne hierboven nog eens. De lengte L is een continue stochast. De kromme is een benadering van de grafiek van de bijpassende kansdichtheidsfunctie. De benadering wordt beter als je meer klassen maakt. De grafiek heeft een mooie klokvorm die wordt bepaald door gemiddelde μ(L) = 182 cm en standaardafwijking σ(L) = 7 cm.

Je zegt dan dat L normaal verdeeld is. De bijbehorende kansen zien er uit als:

• P(165 ≤ L < 180)
• P(L < 180)
• P(L > 186)

Dergelijke cumulatieve kansen kan de grafische rekenmachine voor je berekenen.

‡

Opgaven

1. Bestudeer de Uitleg. Bekijk het histogram van de lengteverdeling van de soldaten.
   1. Hoeveel bedraagt `text(P)(165 <= L < 180)` volgens het histogram? Geef je antwoord als getal tussen 0 en 1.
   Deze kans kun je ook bepalen door uit te gaan van de normaalkromme als model voor de lengteverdeling van de soldaten. Je grafische rekenmachine kent de normale verdeling. Je schrijft de gevraagde kans vaak als `text(P)(165 <= L < 180 | mu(L) = 182 text( en ) sigma(L) = 7)`. De vier getallen in deze uitdrukking moet je in de grafische rekenmachine in de juiste volgorde in de normaalverdeling invoeren. Bekijk het practicum via

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Continue kansmodellen > Normale kansen > Practicum

   Ga naar het onderdeel "De normale kansverdeling".
   2. Bepaal `text(P)(165 <= L < 180 | mu(L) = 182 text( en ) sigma(L) = 7)`.
   3. Bereken de kans dat een soldaat tussen 166 en 177 cm lang is.
   4. Bereken hoeveel procent van de soldaten kleiner dan 166 cm is.
   5. Bereken hoeveel procent van de soldaten langer dan 192 cm is.


2. Kijk weer naar de lengteverdeling van de soldaten. Hun gemiddelde lengte is 182 cm.
   1. Controleer de vuistregels met behulp van je grafische rekenmachine.
   2. Hoeveel procent van de soldaten heeft volgens de normaalkromme een lengte die minder dan drie standaarddeviaties van het gemiddelde afwijkt?

Theorie

Continue stochasten zoals lengte, gewicht, inhoud, etc., zijn vaak normaal verdeeld. De normaalkromme (de grafiek van de bijpassende kansdichtheidsfunctie) wordt bepaald door het gemiddelde μ en de standaardafwijking σ van de stochast. In je rekenmachine is de formule voor die normaalkromme geprogrammeerd. Hij kan daarom de normaalkromme voor je tekenen.

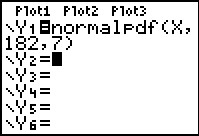
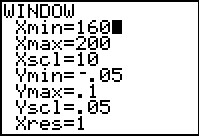
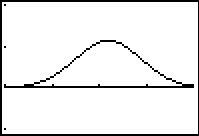
De bijbehorende normale kansen zijn te vinden door de oppervlakte te berekenen van het juiste gebied onder de normaalkromme. Zo is in de applet aangegeven:
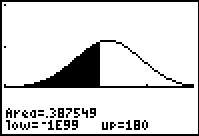
P(165 ≤ L ≤ 180) ≈ 0,380

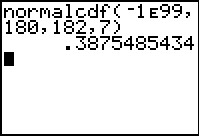
De GR kan dergelijke kansen rechtstreeks berekenen. Ook kan hij het bijbehorende gebied voor je schaduwen.

‡

Voorbeeld 1

De lengte L van een groep soldaten is normaal verdeeld met een gemiddelde van μ = `bar L` = 182 cm en een standaarddeviatie van σ = 7 cm.

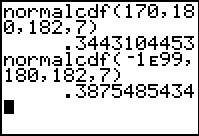
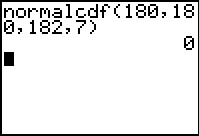
Bereken P(170 ≤ L ≤ 180), P(L < 180),
P(L = 180) en P(L ≥ 180).

Antwoord

Al deze kansen zijn met de GR gemakkelijk te vinden, zie ook het Practicum.

• P(170 ≤ L ≤ 180) ≈ 0,3443
• P(L < 180) ≈ 0,3875
• P(L = 180) = 0
• P(L ≥ 180) = 1 – P(L < 180) ≈ 0,6125

‡

Voorbeeld 2

Het gewicht G van een bepaalde soort appels is normaal verdeeld met een gemiddeld van 150 gram en een standaarddeviatie van 17 gram. Hoeveel procent van deze appels weegt meer dan 160 gram?

Antwoord

Deze vraag kun je vertalen naar: "Bereken P(G > 160 | μ = 150 en σ = 17)."

Met je GR vind je: P(G > 160 | μ = 150 en σ = 17) ≈ 0,2781.

En dus is ongeveer 28% van deze appels zwaarder dan 160 gram.

‡

Voorbeeld 3

De lengte L van een groep soldaten is normaal verdeeld met een gemiddelde van
μ = `bar L` = 182 cm en een standaarddeviatie van σ = 7 cm.

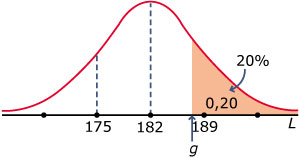
Welke lengtes kunnen de 20% langste mensen in deze groep aannemen?

Antwoord

Deze vraag kun je vertalen in:
Bereken g als je weet dat P(L ≥ g) = 0,20.

De grafische rekenmachine heeft hiervoor een speciale functie ingebouwd gekregen. Die stelt je in staat om vanuit een gegeven kans de grenswaarde terug te vinden. Alleen is die functie wel ingesteld op "kleiner-of-gelijk"-kansen.

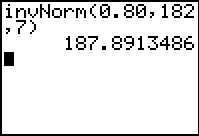
Omdat P(L ≥ g) = 0,20 betekent dat P(L ≤ g) = 1 – 0,20 = 0,80 kun je die functie hier toch gebruiken.
Je vindt: g ≈ 187,9.
De 20% langste mensen zijn 187,9 cm of langer.

‡

Opgaven

3. In Voorbeeld 1 zie je nog eens hoe je bij de lengteverdeling van de soldaten kansen berekend uitgaande van een normale verdeling als model.
   1. Wat betekent `text(P)(162 < L < 178)` in dit verband?
   2. Hoeveel procent van de soldaten heeft een lengte tussen 171 en 178 cm?
   3. Hoeveel procent van de soldaten heeft een lengte van precies 171 cm?
   Bij deze laatste vraag ben je hopelijk een probleem tegengekomen dat bij het werken met normale verdelingen een rol speelt. De gegevens van de soldaten zijn op hele lengtes afgerond. Als je dus vraagt naar het percentage soldaten met een lengte van precies 171 cm, dan moet je goed afspreken wat je bedoeld: echt precies 171 cm, of afgerond 171 cm.
   4. Wat is het antwoord op c wanneer je wilt weten hoeveel procent van de soldaten een lengte heeft van afgerond 171 cm?
   5. Wat betekent dit afrondingsprobleem voor het antwoord op b?
   Vanaf nu moet je de afspraak hanteren dat je bij een normale verdelingen geen rekening houdt met afrondingen, tenzij duidelijk in de vraagstelling naar voren komt dat dit moet. Dit betekent dat `text(P)(162 < L < 178) = text(P)(162 <= L < 178) = text(P)(162 < L <= 178) = text(P)(162 <= L <= 178)`.
   6. Hoeveel procent van de soldaten van deze kazerne heeft een lengte van minder dan 158 cm?
   7. Hoeveel procent van de soldaten van deze kazerne heeft een lengte vanaf `mu - 1,5 * sigma` t/m `mu + 1,5 * sigma`?


4. Het gewicht `G` van een bepaalde soort appels is normaal verdeeld met een gemiddeld van 150 gram en een standaarddeviatie van 17 gram. Bekijk eventueel Voorbeeld 2.
   1. Hoe groot is de kans dat een appel van deze soort minder dan 140 gram weegt?
   2. Hoeveel procent van deze appels heeft een gewicht dat minder dan 10 afwijkt van het gemiddelde?
   3. Een groenteboer heeft nog 340 van die appels. Hoeveel daarvan zijn lichter dan 120 gram?


5. Bioloog Peter Adriaanse heeft van 1000 koolwitjes de spanwijdte van de vleugels gemeten. Hij vond dat deze spanwijdte ongeveer normaal is verdeeld met een gemiddelde van 5,2 cm en een standaardafwijking van 0,8 cm.
   1. Hoeveel procent van de gemeten koolwitjes had een spanwijdte van meer dan 6 cm?
   2. Hoeveel van de gemeten koolwitjes hadden een spanwijdte tussen de 5 en de 6 cm?
   3. Hoe groot is de kans op een koolwitje met een spanwijdte van minstens 6,5 cm?


6. In Voorbeeld 3 zie je hoe je met de rekenmachine bij gegeven kansen de grenswaarde kunt terugvinden.
   1. Voer zelf de berekening in dit voorbeeld uit.
   2. Hoe lang zijn de 20% kleinste soldaten op zijn hoogst?
   3. 10% van de soldaten zit boven het gemiddelde maar is toch niet langer dan `a` cm. Bereken `a`.


7. Ga nog eens uit van de normaal verdeelde lengtes van de soldaten in een bepaalde kazerne. De gemiddelde lengte is 182 cm en de standaardafwijking is 7. Men besluit voor deze 1200 soldaten T-shirts aan te schaffen in drie maten: S (small), M (medium) en L (large). Deze maten worden zo gemaakt dat elke maat precies voor `1/3` deel van de soldaten geschikt is.
   1. Voor welke lengtes is maat S geschikt?
   2. Voor welke lengtes is maat M geschikt?

Verwerken

8. Een vulmachine vult kilopakken rijst. Het ingestelde vulgewicht van de machine komt overeen met het gemiddelde gewicht van de pakken rijst. De gewichten zijn normaal verdeeld. Het gemiddelde gewicht van een pak rijst is 1010 gram en de standaardafwijking is 9 gram.
   1. Hoeveel procent van pakken weegt minder dan 1000 gram?
   2. Hoeveel procent van de pakken weegt meer dan 1000 gram?
   3. Hoe groot is de kans op een pak dat meer dan 5 gram te zwaar is?
   4. Hoeveel procent van de pakken is meer dan 20 gram te zwaar?


9. Aan een havo examen wiskunde A nemen 20 000 kandidaten deel. De resultaten zijn ongeveer normaal verdeeld. Het gemiddelde cijfer is 6,4 en de standaardafwijking 1,1.
   1. Hoeveel kandidaten hebben een cijfer onder de 5,5, dus een onvoldoende?
   2. Hoeveel kandidaten hebben minstens een 7,0?
   3. Hoeveel kandidaten hebben hoogstens een 4,0?


10. Het vulvolume `V` van een pak melk is normaal verdeeld met een gemiddelde van 1,02 liter en een standaardafwijking van 0,015 liter. De consument verwacht 1 liter melk te kopen.
    1. Hoeveel procent van de melkpakken bevat minder dan 1 liter melk?
    2. Hoeveel procent van de melkpakken bevat meer dan 1,03 liter melk?
    3. Je koopt zo’n melkpak. Wat is de kans dat er 2 centiliter te weinig melk in je pak zit?
    4. Je kunt niet bepalen hoeveel procent van de melkpakken een inhoud van precies 1 liter heeft. Je kunt wel bepalen hoeveel procent van de melkpakken afgerond op twee decimalen 1 liter bevat. Dan zie je dat het gaat om het gebied vanaf de grens 0,995 tot de grens 1,005. En daar hoort wel degelijk een bepaald percentage bij. Bereken dat percentage.
    5. 5% van de melkpakken heeft een vulvolume van minder dan g. Bereken g.
    6. Hoeveel liter melk bevat een melkpak dat hoort bij de volste 10%?


11. Volgens het onderzoek van Freudenthal en Sittig uit 1947 waren de lengtes van vrouwen die bij de Bijenkorf winkelden normaal verdeeld met een gemiddelde van 162 cm en een standaarddeviatie van 6,5 cm. Ga bij het beantwoorden van de onderstaande vragen steeds uit van die normale verdeling als model voor de lichaamslengte van deze 5001 vrouwen.
    
    
    
    
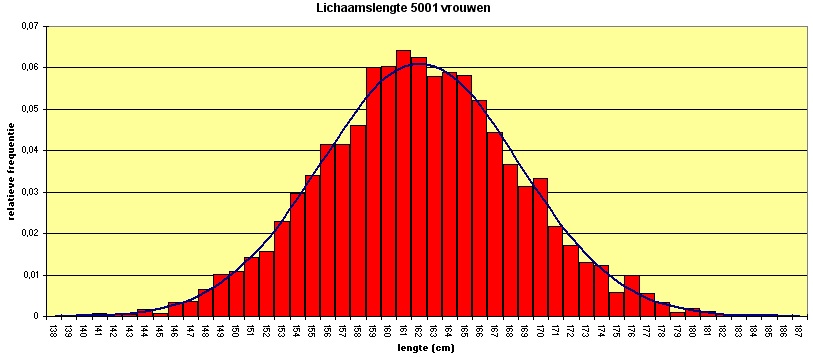
    1. Hoeveel procent van deze vrouwen was langer dan 170 cm?
    2. Hoeveel procent van deze vrouwen had een lengte tussen 160 en 170 cm?
    3. Hoe groot is de kans dat een vrouw die je toen bij de Bijenkorf tegen kon komen 160 cm lang was? (Neem aan dat alle lengtes op gehele cm zijn afgerond.)
    4. Hoe lang waren de 10% kleinste vrouwen?
    5. En hoe lang waren de 10% langste vrouwen?


12. Open het bestand "Enkele lichaamsafmetingen van 5001 vrouwen uit 1947" op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Continue kansmodellen > Totaalbeeld > Toepassingen

    Hierin zie je een tabel met kniehoogtes in cm van de 5001 vrouwen uit het onderzoek in 1947 van Freudenthal en Sittig in opdracht van De Bijenkorf.
    1. Bereken met de computer de gemiddelde kniehoogte en de standaarddeviatie.
    2. Teken een histogram en benader dit met een normaalkromme waarin je beide waarden aangeeft.
    Neem nu verder aan dat de kniehoogte `K` van vrouwen normaal is verdeeld met de eerder berekende waarden voor het gemiddelde `mu` en de standaarddeviatie `sigma`.
    3. 90% van de kniehoogtes zit tussen `mu – a` en `mu + a`. Hoe groot is `a`?
    4. Welke minimale lengte hebben de 20% grootste kniehoogtes?

Testen

13. Een zakje Cup-a-soup moet 17 g bevatten. Het gewicht van zakjes is normaal verdeeld. De vulmachine is zo ingesteld dat het vulgewicht 19 g bedraagt met een standaardafwijking van 1,5 g. Het vulgewicht komt overeen met het gemiddelde gewicht.
    1. Hoe groot is de kans dat een zakje minder dan 17 g weegt?
    2. Hoe groot is de kans dat een zakje Cup-a-Soup meer dan 17 g weegt?
    3. Hoeveel weegt 90% van deze zakjes op zijn hoogst?
    4. Hoeveel weegt 90% van deze zakjes op zijn minst?


14. Bij een groep van 1000 mannen is de bloeddruk normaal verdeeld met een gemiddelde van 128,5 mm Hg met een standaardafwijking van 12,5 mm Hg.
    1. Hoeveel mannen hebben een bloeddruk die meer dan drie keer de standaardafwijking afwijkt van de gemiddelde bloeddruk?
    2. Hoeveel procent van de mannen heeft een bloeddruk van meer dan 150?
    3. Hoeveel bedraagt de bloeddruk van de 10% mannen met de hoogste bloeddruk?