
Wortel-n-wet
Inleiding
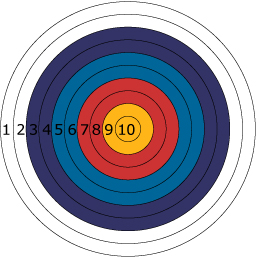
Je hebt al eerder gezien dat je een kansverdeling kunt opstellen voor het boogschieten met één pijl op deze roos. Maar vaak schiet je vaker, bijvoorbeeld 20 keer, en kijk je naar het totaal aantal punten of het gemiddelde aantal punten.
En hoe zit het dan met de verwachting en de standaarddeviatie?
Je leert nu:
- werken met een herhaling van steeds dezelfde stochast;
- regels voor de verwachting en de standaardafwijking van een herhaling van stochasten.
Je kunt al:
- een kansverdeling opstellen bij een stochast;
- de regels voor de verwachting en de standaarddeviate van de som van twee stochasten.
Verkennen
Je schiet 20 keer op de roos (0, 1, 2, ..., 10 punten te behalen)
Je kansverdeling per schot is:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(X = x) | 0,02 | 0,02 | 0,04 | 0,10 | 0,09 | 0,11 | 0,12 | 0,12 | 0,15 | 0,15 | 0,08 |
Je kent de regels voor de verwachting en de standaardafwijking van de som van twee stochasten.
> Hoeveel punten verwacht je in totaal te scoren? En welke standaardafwijking hoort er bij dit totaal?
> Hoeveel punten verwacht je gemiddeld per schot te scoren? En welke standaardafwijking hoort daar bij?
Uitleg
Je schiet 20 keer op de roos (0, 1, 2, ..., 10 punten te behalen).
Je kansverdeling per schot is:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(X = x) | 0,02 | 0,02 | 0,04 | 0,10 | 0,09 | 0,11 | 0,12 | 0,12 | 0,15 | 0,15 | 0,08 |
De verwachting per schot is 6,22 punten met een standaardafwijking van 2,56 punten.
Omdat elk schot onafhankelijk is van het voorgaande kun je zowel de optelregel voor verwachtingswaarden als die voor varianties toepassen:
E(20X) = E(X + X + ... + X) = E(X) + E(X) + ... + E(X) = 20 · E(X)
en
Var(20X) = Var(X + X + ... + X) = Var(X) + Var(X) + ... + Var(X) = 20 · Var(X).
Dus bij het totaal van 20 schoten is:
- de verwachtingswaarde E(20X) = 20 · 6,22 = 124,4 punten
- de standaarddeviatie σ(20X) = ≈ 11,45 punten.
Voor het gemiddelde aantal punten per schot deel je deze getallen door 20. De verwachting wordt dan natuurlijk weer 6,22. Maar de standaardafwijking wordt ongeveer ≈ 0,57 en dus veel kleiner dan bij één schot.
‡
Opgaven
-
In de Uitleg is `X` het aantal punten dat je per schot kunt behalen bij het boogschieten op een roos.
Schiet je 12 keer op die roos, dan heb je het over de stochast `12X`.
-
Controleer dat E`(X) ~~ 6,22` en `sigma(X) ~~ 2,56`.
-
Hoeveel punten verwacht je te halen als je 12 keer op die roos schiet? En met welke standaardafwijking?
-
Hoeveel punten verwacht je gemiddeld per schot te halen als je 12 keer op die roos schiet? Met welke standaardafwijking?
-
Ligt het voor de hand dat de standaardafwijking kleiner wordt naarmate je vaker op de roos schiet?
-
`X` stelt het aantal ogen op een dobbelsteen voor.
-
`2X` stelt het aantal ogen voor als je met twee dobbelstenen werpt. Bereken E`(2X)` en `sigma(2X)`.
-
Welk verband is er tussen E`(X)` en E`(2X)` en tussen `sigma(X)` en `sigma(2X)`?
-
`M` is het gemiddelde aantal ogen per worp als je met twee dobbelstenen werpt.
Bereken E`(M)` en `sigma(M)`.
-
Welk verband is er tussen E`(X)` en E`(M)` en tussen `sigma(X)` en `sigma(M)`?
-
In een doos zitten vijf balletjes met daarop de getallen 2, 3, 5, 7 en 12.
-
Bereken de verwachtingswaarde en de standaardafwijking voor het getal dat je krijgt bij het aselect trekken van één balletje.
-
Je trekt twee balletjes met teruglegging. Welke mogelijke getalcombinaties kun je daarbij aantreffen?
Bepaal van alle mogelijke tweetallen het gemiddelde. Bepaal van deze gemiddelden de verwachtingswaarde en de standaardafwijking.
-
Welk verband bestaat er tussen de verwachtingswaarden die je bij a en b hebt berekend?
-
Laat zien dat je de standaardafwijking bij b ook had kunnen vinden door de standaardafwijking van a te delen door `sqrt(2)`. Geef hiervoor een verklaring.
Theorie
Heb je te maken met n onafhankelijke gelijke kansexperimenten, elk met dezelfde stochast X, dan geldt voor de som van deze n stochasten:
- E(n · X) = n · E(X)
- σ(n · X) = · σ(X)
Het bewijs hiervan verloopt op dezelfde wijze als in de Uitleg.
Je noemt deze stelling de -wet.
Voor de kansverdeling die hoort bij het gemiddelde van n onafhankelijke gelijke kansexperimenten elk met stochast X geldt daarom:
- E() = = E(X)
- σ() =
‡
Voorbeeld 1
Op doosjes paperclips van een bepaald merk staat: ca. 100 stuks.
Door tellingen is gebleken dat er in deze doosjes gemiddeld 104,3 paperclips zitten met een standaardafwijking van 3,5. Je haalt 10 doosjes van die paperclips. Hoeveel mag je er dan in totaal verwachten en met welke standaardafwijking?
Antwoord
Neem aan dat het aantal paperclips X in elk doosje niet afhangt van het aantal in de andere doosjes.
Dan geldt:
- E(10X) = 10 · E(X) = 10 · 104,3 = 1043
- σ(10X) = · σ(X) = · 3,5 ≈ 11,1.
Je mag daarom 1043 paperclips verwachten met een standaardafwijking van ongeveer 11,1.
‡
Voorbeeld 2
Op doosjes paperclips van een bepaald merk staat: ca. 100 stuks.
Door tellingen is gebleken dat er in deze doosjes gemiddeld 104,3 paperclips zitten met een standaardafwijking van 3,5. Je haalt 10 doosjes van die paperclips. Hoeveel mag je er dan gemiddeld per doosje verwachten en met welke standaardafwijking?
Antwoord
Neem aan dat het aantal paperclips X in elk doosje niet afhangt van het aantal in de andere doosjes.
Dan geldt:
- E(10X) = 10 · E(X) = 10 · 104,3 = 1043
- σ(10X) = · σ(X) = · 3,5 ≈ 11,1.
Je mag daarom 1043 paperclips verwachten met een standaardafwijking van ongeveer 11,1.
Voor het gemiddelde aantal per doosje geldt:
- E() = = = 104,3
- σ() = = = ≈ 1,1
‡
Opgaven
-
In een doosje paperclips zitten gemiddeld 104,3 paperclips met een standaardafwijking van 3,5. Je koopt 5 van die doosjes paperclips. Zie Voorbeeld 1.
- Hoeveel paperclips mag je in totaal verwachten in de 5 doosjes samen?
- Welke standaardafwijking heeft het aantal paperclips in deze 5 doosjes samen?
-
In een doosje paperclips zitten gemiddeld 104,3 paperclips met een standaardafwijking van 3,5. Je koopt 5 van die doosjes paperclips. Zie Voorbeeld 2.
- Hoeveel paperclips mag je gemiddeld per doosje verwachten in deze steekproef van 5 doosjes?
- Welke standaardafwijking heeft het gemiddelde aantal paperclips per doosje in deze steekproef van 5 doosjes?
-
In een fabriek worden pakken met 1 kg meel gevuld. De vulmachine is afgesteld op een gemiddeld vulgewicht van 1002 g met een standaardafwijking van 4 g.
De pakken worden op hun beurt verpakt met een plastic folie in pakketten van 10 pakken.
- Bereken het gemiddelde gewicht van deze pakketten.
- Welke standaardafwijking geldt voor het gewicht van deze pakketten?
- Welke verwachtingswaarde en standaardafwijking geldt voor één pak meel uit zo’n pakket?
Op een pallet worden 100 pakketten geplaatst.
- Welk gewicht verwacht je dat op het pallet geplaatst is en welke standaardafwijking geldt hiervoor?
- Welke verwachtingswaarde en standaardafwijking gelden voor een pak meel dat uit een pallet genomen wordt?
Verwerken
-
Een bepaald type DVD-recorder wordt in dozen verpakt die een gemiddelde hoogte
van 10 cm hebben met een standaardafwijking van 4 mm.
Bij een groothandel wordt een aantal van deze dozen in een magazijn opgeslagen.
- Er worden 15 dozen op elkaar geplaatst. Bereken de verwachtingswaarde van de hoogte en geef de bijbehorende standaardafwijking.
- Bij het vervoer van deze dozen gebruikt men een vrachtwagen met een hoogte van 2,5 m en een standaardafwijking van 1,9 cm.
Bij het beladen van deze vrachtwagen maakt men stapels van 25 dozen. Welke standaardafwijking voor de hoogte mag een doos hebben?
-
Vierkante postzegels kunnen gekocht worden op rollen van 500 zegels. Een rol
heeft een lengte van 15 m met een standaardafwijking van 5 mm.
- Welke afmetingen hebben de zegels gemiddeld?
- Wat is de standaardafwijking van de lengte van één zegel?
Dezelfde zegels zijn ook verkrijgbaar op vellen van 10 bij 20 zegels.
- Welke afmetingen (lengte en breedte) verwacht je dat deze vellen hebben? Met welke standaardafwijkingen?
-
Een tuinder heeft 10.000 jonge preiplanten geteeld voor de verkoop. Uit ervaring
weet hij dat de kans dat zo’n plantje bij de klant begint te groeien en geoogst kan
worden 0,8 is.
- Hoe groot is de kans dat 30 van de 50 planten, die iemand bij deze tuinder heeft gekocht voor zijn tuin, ook echt geoogst kunnen worden?
- Welk aantal planten mag deze klant verwachten te oogsten? Met welke standaardafwijking?
- Welk aantal planten verwacht de tuinder dat uiteindelijk kan worden geoogst van zijn totale hoeveelheid? Met welke standaardafwijking moet hij rekening houden?
Testen
-
In een doos zitten vier kaartjes met daarop de getallen 3, 7, 11 en 15.
- Bereken de verwachtingswaarde en de standaardafwijking voor het getal bij het trekken van één kaartje uit de doos.
- Bereken vanuit de bijbehorende kansverdeling de verwachtingswaarde van de som van de getallen van twee getrokken kaartjes. Bereken voor deze som ook de standaardafwijking.
- Welk verband bestaat er met de verwachtingswaarde en de standaardafwijking die je bij a hebt berekend?
- Bereken vanuit de bijbehorende kansverdeling de verwachtingswaarde en de standaardafwijking van het gemiddelde van de getallen op twee getrokken kaartjes.
Welk verband bestaat er nu met de verwachtingswaarde en de standaardafwijking die je bij a hebt berekend?
- Trek met teruglegging drie kaartjes uit de doos. Bereken de verwachtingswaarde en de standaardafwijking van de som en van het gemiddelde van de getallen op de drie getrokken kaartjes.
-
In de maand december zijn er kerstzegels verkrijgbaar. Ze worden in een bepaald
jaar aangeboden op een velletje van vier bij vijf zegels.
De afmetingen van de velletjes zijn 15,5 bij 15,5 cm met een standaardafwijking
van 0,75 mm in beide richtingen.
Bereken de afmetingen en de standaardafwijkingen van deze zegels.

