Uitspraken doen

Inleiding

Een statistisch onderzoek is opgezet om uitspraken te kunnen doen.
In kranten en tijdschriften staat het er bol van. Maar vaak ontbreekt belangrijke informatie: bijvoorbeeld staat er wel een gemiddelde, maar wordt er geen spreidingsmaat vermeld. Of, er wordt niet vermeld hoe de steekproef is samengesteld...
Welke uitspraken kun je wel doen en welke niet?
En wat moet je allemaal vermelden om de betrouwbaarheid van een uitspraak duidelijk te maken?

Je leert nu:

• welke uitspraken je kunt doen;
• kritisch te kijken naar uitspraken die je tegen komt.

Je kunt al:

• allerlei statistische diagrammen, waar onder een boxplot maken;
• centrummaten en spreidingsmaten berekenen.

Verkennen

Het CBS (Centraal Bureau voor de Statistiek) verzamelt cijfers over de meest uitlopende thema’s. Op de site http://www.cbs.nl kun je dat allemaal terugvinden. Bekijk ook recente publicaties van het CBS en persberichten van het CBS.

Zoek een recente publicatie of een recent persbericht en achterhaal hoe dit bericht in de media (kranten, tijdschriften, radio, televisie) gepresenteerd is. Maak bij een publicatie of persbericht een goede betrouwbare kop voor boven een krantenartikel over dit onderwerp.

Uitleg

Hier zie je de lengteverdeling van een groep soldaten op een bepaalde kazerne.

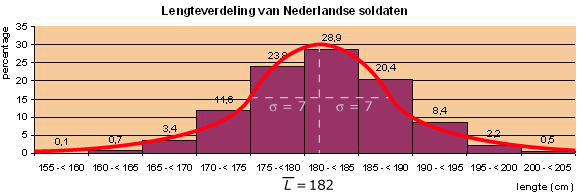
Het histogram of het bijbehorende frequentiepolygoon krijgt bij zoveel waarnemingen een mooie klokvorm. Bij veel continue variabelen, bijvoorbeeld bij gewicht en lengte of inhoud, krijg je zo'n klokvormige frequentieverdeling. De vorm ervan wordt bepaald door gemiddelde en standaardafwijking. Je kunt dan met behulp van gemiddelde en standaardafwijking twee algemene uitspraken doen. Deze uitspraken zijn vuistregels.

• vuistregel 1: tussen $\overline{x}-{\sigma }_x$ en $\overline{x}+{\sigma }_x$ zit 68% van de waarnemingsgetallen.
• vuistregel 2: tussen $\overline{x}-2{\sigma }_x$  en $\overline{x}+2{\sigma }_x$ zit 95% van de waarnemingsgetallen.

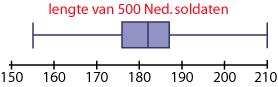
Bij de groep van 500 Nederlandse soldaten kun je ook een boxplot van de lengteverdeling maken.

Je kunt uit dit boxplot concluderen dat 25% van de soldaten tussen Q₁ = 176 en Q₂ = 182 en dat 50% van deze mannen tussen Q₁ = 176 en Q₃ = 187 cm is. Ook deze uitspraken kun je alleen doen over de steekproef van 500 soldaten.

Het doel van statistisch onderzoek is om uitspraken te doen over een bepaalde populatie. Op grond van een steekproef kun je daar alleen verantwoord uitspraken over doen als deze steekproef echt een doorsnede van de populatie is. Maar ook de beste steekproef blijft slechts een steekproef. Je zult steeds rekening moeten houden met een zekere speling: de onbetrouwbaarheidsmarge.
Onderzoek je hoeveel procent van de scholieren in de vierde klas een bepaald nieuw type muziekspeler wil kopen zodra dat op de markt komt? Vul dan bij de berekening van de steekproefmarges van het NIPO de gegevens van twee peilingen in: het percentage in twee steekproeven uit de populatie scholieren in de vierde klas. Je zult zien: hoe groter de steekproef, hoe groter de betrouwbaarheid van je conclusie. Je noemt dat een significante conclusie. Maar dan nog hangt alles af van de kwaliteit van je steekproef.

Statistiek lijkt spijkerhard maar je kunt sneller misleid worden door diagrammen en cijfers dan je denkt. Soms wordt een deel van een diagram of van een as weggelaten. Of de cijfers en uitspraken gaan over een te kleine of verkeerde steekproef. Wees altijd op je hoede met cijfers en diagrammen bij een onderzoek. Zelden hoor je dat uit een onderzoek geen conclusies getrokken kunnen of mogen worden...

Opgaven

1. Bestudeer de Uitleg, pagina 1.
   Gebruik de lengteverdeling van 90 meisjes die je kunt vinden via

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen

   1. Maak van het histogram een frequentiepolygoon en print de figuur.
   2. Teken met de hand de bijpassende klokvormige verdeling er in. Gebruik het gemiddelde en de standaardafwijking van de gegeven lengteverdeling.
   3. Onderzoek of voor de gegeven lengteverdeling de 68%-vuistregel geldt.
   4. Onderzoek of voor de gegeven lengteverdeling de 95%-vuistregel geldt.
   5. Is de klokvormige verdeling een goede benadering voor de lengteverdeling van deze 90 meisjes?


2. Op grond van een representatieve steekproef uit alle Nederlandse meisjes heeft een onderzoeksbureau geconcludeerd dat hun lengtes klokvormig verdeeld zijn met een gemiddelde lengte van 172 cm en een standaardafwijking van 6 cm.
   1. Bepaal m.b.v. de vuistregels hoeveel procent van de Nederlandse meisjes dan langer is dan `172 + 6 = 178` cm.
   2. Bepaal zo ook hoeveel procent korter is dan `172 - 2 * 6 = 160` cm.


3. Bestudeer de Uitleg, pagina 2.
   Hier staat een aantal conclusies getrokken uit statistische gegevens. Geef telkens commentaar op de uitspraak.
   1. In 1971 nam de NAVO 49% van alle militaire uitgaven voor haar rekening. In 1981 was dat nog 43%. De militaire uitgaven van de NAVO zijn in 1981 lager dan in 1971.
   2. Van alle verkeersongelukken op deze weg blijkt bij 25% alcohol een rol te hebben gespeeld. De conclusie is dat rijden met alcohol op veiliger is dan zonder alcohol.
   3. Wasmiddel XXX wast 20% witter dan alle andere wasmiddelen.
   4. School A heeft hogere percentages geslaagden dan school B. Conclusie: je kunt beter op school A zitten als je snel wilt slagen.

Theorie

In elk deel van een boxplot zit 25% van de waarnemingen.
Wanneer het histogram of bijbehorende frequentiepolygoon bij benadering klokvormig is, dan zijn het gemiddelde $\overline{x}$  en de standaardafwijking ${\sigma }_x$ goede karakteristieken van de frequentieverdeling. En er gelden de volgende vuistregels:

• vuistregel 1: tussen $\overline{x}-{\sigma }_x$ en $\overline{x}+{\sigma }_x$ zit 68% van de waarnemingsgetallen.
• vuistregel 2: tussen $\overline{x}-2{\sigma }_x$  en $\overline{x}+2{\sigma }_x$ zit 95% van de waarnemingsgetallen.

De uitspraken die je doet over je steekproef zijn alleen geldig voor de gehele populatie als de steekproef een goede afspiegeling is van die populatie, dus representatief is. De uitspraken zijn betrouwbaarder als de steekproef voldoende groot is.
Wees altijd alert bij uitspraken naar aanleiding van diagrammen, presentaties van cijfers en conclusies uit onderzoek. Ook populaire 'vertalingen' van onderzoeksrapporten in tijdschriften en kranten door journalisten zijn niet altijd betrouwbare uitspraken.

Voorbeeld 1

De lengteverdeling van Nederlandse mannen boven 20 jaar is bij benadering klokvormig.
De gemiddelde lengte is 180,3 cm.
De standaardafwijking is 7,74 cm.

Tussen welke twee lengtes zit volgens de vuistregels 68% van de Nederlandse mannen? En 95%?

Antwoord

Volgens de vuistregels zit 68% van deze mannen tussen de gemiddelde lengte min de standaardafwijking en de gemiddelde lengte plus de standaardafwijking.
Dus 68% heeft een lengte tussen 172,5 cm en 188,0 cm.

Bij de 95%-regel moet je 2 keer de standaardafwijking van het gemiddelde afzitten.
Dus heeft 95% een lengte tussen 164,8 cm en 195,8 cm.

Voorbeeld 2

Enkele voorbeelden van misleidingen...

Voorbeeld 3

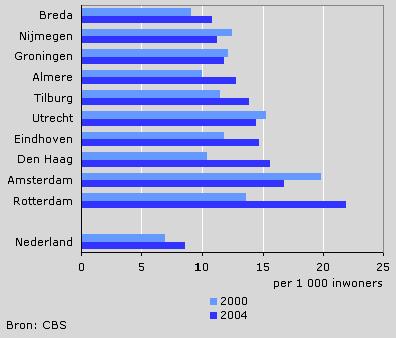
Door te klikken op het plaatje zie je twee diagrammen over criminaliteit.
De NRC meldt naar aanleiding van deze gegevens "Criminaliteit grote steden weer gedaald". Het Parool schrijft daarover "Meer geweld in grote steden". De koppen lijken elkaar tegen te spreken. Welke kop zou jij erbij verzinnen?

Geweldscriminaliteit

Opgaven

4. Bekijk Voorbeeld 1.
   Laat zien dat de verdeling van lengte `L` van de Nederlandse mannen boven de 20 jaar inderdaad klokvormig is. Teken een bijpassende frequentiepolygoon en reken zelf het gemiddelde `bar(L)` en de standaardafwijking `sigma_L` na.
   Ga ook zelf na, dat beide vuistregels ongeveer kloppen.
   


5. Voor een onderzoek naar de levensduur van batterijen is op basis van 20 waarnemingen een boxplot getekend.
   
   
   
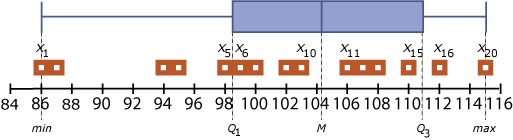
   Geef aan of de volgende uitspraken waar of niet waar zijn.
   1. Minimaal 25% van de batterijen gaat langer dan 110 minuten mee.
   2. 50 % van de batterijen heeft een levensduur van 104 minuten.
   3. De batterijen gaan gegarandeerd 1,5 uur mee.
   4. Minimaal 75% van de batterijen is na 112 minuten leeg.


6. Op de verpakking van een pak koffie staat een inhoud van 250 gram. In werkelijkheid wil dat nog wel eens iets meer of minder zijn. Het gewicht van 1000 pakken koffie wordt gemeten, zonder verpakking. Uit de metingen blijkt een gemiddeld gewicht van 254 gram. De standaardafwijking is 4. We gaan er van uit dat de verdeling van het gewicht klokvormig is. Geef met behulp van de vuistregels bij de volgende uitspraken aan of ze waar of niet-waar zijn.
   1. Ongeveer 95% van de pakken koffie heeft een gewicht tussen 246 en 262 gram.
   2. Ongeveer 5 % heeft een gewicht onder 246 gram.
   3. Ongeveer 16% van de pakken koffie bevat minder dan de beloofde 250 gram inhoud.
   4. Ongeveer 50% van de pakken koffie heeft een gewicht van 250 gram.
   5. Minimaal 75% van de pakken koffie bevat meer dan 250 gram.


7. In Voorbeeld 2 en Voorbeeld 3 kun je zien hoe slordige statistieken je kunnen misleiden en/of hoe soms slordige conclusies worden getrokken.
   Geef bij elk van de voorbeelden kort commentaar.
   


8. Tien procent van de Nederlanders is racistisch, zo bleek begin juni uit een opinieonderzoek uitgevoerd in opdracht van de grote regionale dagbladen.
   Hans van Maanen, wetenschapsjournalist bekeek dit onderzoek eens wat beter.
   (Zie http://www.vanmaanen.org/hans/columns/racisme.html)
   Lees zijn artikel en beantwoord de volgende vragen.
   1. Welke twee vragen komen bij Hans van Maanen op bij de resultaten?
   2. Hoeveel mensen deden mee aan het onderzoek?
   3. Hoeveel vragenlijsten zijn er verstuurd en hoeveel daarvan zijn ingevuld?
   4. Er worden voorbeelden gegeven van stellingen die in de vragenlijst stonden. Welke?
   5. Welk commentaar kun je hebben op deze stellingen, waardoor ze zo moeilijk te beantwoorden zijn?
   6. Wat vindt Hans van Maanen van de wijze waarop de resultaten in het nieuws zijn gebracht?


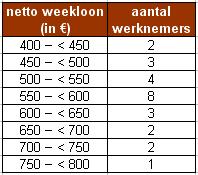9. Een bedrijf heeft 25 werknemers in vaste dienst met een volledige werkweek. De netto weeklonen van deze werknemers zijn verwerkt in deze frequentietabel.
   1. Bepaal het gemiddelde en de standaardafwijking van deze verdeling.
   2. Maak bij de frequentietabel een relatief cumulatieve frequentietabel en teken de bijbehorende een kleiner-gelijk-kromme.
   3. Gebruik de kleiner-gelijk-kromme om het gemiddelde af te lezen. Geef aan hoe je dat doet.
   4. Bepaal met behulp van de kleiner-gelijk-kromme de standaardafwijking. Geef aan hoe je dat doet. Vergelijk je antwoord met dat in a.
   5. Hoeveel procent van alle weeklonen wijkt meer dan twee standaarddeviaties af van het gemiddelde? Klopt dit met de vuistregels voor een normale verdeling?

Verwerken

10. In 1951 verscheen bij uitgeverij Stafleu te Leiden het boek "De Juiste Maat", met als ondertitel "Lichaamsafmetingen van Nederlandse vrouwen als basis voor een nieuw maatsysteem voor damesconfectiekleding". Auteurs van dit boek waren J. Sittig, Adviesbureau voor Toegepaste Statistiek en Prof.dr. H. Freudenthal, Rijksuniversiteit Utrecht. Het onderzoek was gehouden in opdracht van N.V. Magazijn De Bijenkorf, Amsterdam.
    In het kader van dit onderzoek zijn bij 5001 vrouwelijke klanten van de Bijenkorf vijftien lichaamsmaten opgemeten. Vervolgens is gekeken welke van deze maten het meest bruikbaar zijn om een maatsysteem voor kleding op te baseren. De verdeling van de lichaamslengten, afgerond op centimeters, vind je via:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen

    1. Maak een bijpassende frequentiepolygoon en een bijpassende cumulatieve frequentiepolygoon.
    2. Bepaal de modale lengte en bereken de gemiddelde lengte.
    3. Bepaal de mediaan en de kwartielen en teken een bijpassend boxplot.
    4. Verdeel de lengten in klassen van 5 cm, te beginnen bij 135 – 139. Maak bij de nieuwe frequentieverdeling opnieuw een frequentiepolygoon. Is deze frequentiepolygoon bij benadering klokvormig?
    5. Bepaal opnieuw de gemiddelde lengte en de mediaan en de kwartielen. Wijken de resultaten veel af van de antwoorden bij b en c?
    6. Hoeveel lengtes verschillen meer dan één keer de standaarddeviatie van het gemiddelde? Hoeveel procent van de vrouwen betreft dit?
    7. Hoeveel procent van de lengtes verschilt meer dan twee keer de standaardafwijking van het gemiddelde?
    8. Komen deze antwoorden overeen met de vuistregels voor klokvormige verdelingen?


11. In een bedrijf is het modale salaris ongeveer €1600,= per maand. Het gemiddelde salaris is €1800,= per maand. Het hoogste salaris is dat van de algemeen directeur. In de boxplot zie je de verdeling van de salarissen over alle 120 mensen die bij het bedrijf werken.
    
    
    
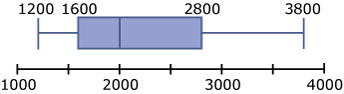
    Bereken in de volgende gevallen telkens weer het modale salaris en het gemiddelde salaris en teken het nieuwe boxplot. Doe voor elk van de drie situaties een kenmerkende uitspraak over de gevolgen van de maatregel voor de laagstbetaalde 25% werknemers.
    1. Alle medewerkers krijgen een loonsverhoging van 3%.
    2. Alle medewerkers krijgen een maandelijkse toeslag van € 200,=.
    3. Het salaris van de algemeen directeur wordt met € 800,= per maand verhoogd.


12. 
    
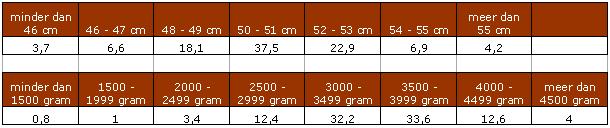
    Hier zie je de gegevens van pasgeboren kinderen in Nederland. Je mag aannemen dat deze verdeling klokvormig is. Doe vier uitspraken met behulp van de vuistregels over geboortegewicht en geboortelengte.
    


13. Het CBS publiceerde in haar webmagazine "Aantal echtscheidingen neemt weer toe". (Bron: http://www.cbs.nl/nl-NL/menu/themas/mens-maatschappij/bevolking/publicaties/artikelen/2006-1862-wm.htm)
    
    
    
    
    1. Teken het diagram van de echtscheidingen voor de periode 1995 – 2005.
    2. Met welk percentage is het aantal echtscheidingen in 2005 toegenomen ten opzichte van 2004?
    3. De Volkskrant kopte "Echtscheidingen na jaren van daling gestegen". Het dagblad Trouw meldde: "Meer echtscheidingen door breekbaar geworden relaties". Welke kop zou jij bij het diagram zetten?
    4. Tineke Fokkema schetste in september 2002 in Demos (zie http://www.nidi.knaw.nl/web/html/public/demos/dm02083.html) het volgende beeld:
       "Na een 20 jaar durende stormachtige groei schommelt het jaarlijkse aantal echtscheidingen in Nederland sinds halverwege de jaren tachtig tussen de 28.000 en de 37.000. (...) In de periode 1965-1985 is het jaarlijkse aantal echtscheidingen sterk toegenomen: van 6.000 tot niet minder dan 34.000."
       Teken een diagram met deze gegevens en die van het CBS voor de periode 1965 – 2005.
    5. Welke kop zou je bij dit diagram plaatsen?
    6. Het Reformatorisch Dagblad plaatst de gegevens van het CBS weer in een heel ander perspectief.
       Zij schreven: "Toch is het veel te vroeg om te concluderen dat het huwelijk weer aan populariteit wint. Het aantal huwelijkssluitingen schommelt nogal, maar daalde het afgelopen decennium sterker dan het aantal echtscheidingen. Tegenover elke 100 gesloten huwelijken stonden in 1993 42 echtscheidingen. In 2005 is dat opgelopen tot 45. Kort door de bocht is de samenvatting: het aantal echtscheidingen daalt omdat er steeds minder te scheiden valt."
       (Bron: http://www.refdag.nl/artikel/1265901/)
       Welke conclusie trekt de journalist van het Reformatorisch Dagblad?


14. Open het Excel bestand met de titel "Patiëntengegevens". Je vindt dit bij

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen

    1. Bereken de gemiddelde lengte van zowel de vrouwelijke als de mannelijke patiënten en de bijbehorende standaardafwijkingen. Is er verschil tussen de lengtes van mannen en vrouwen?
    2. Onderzoek of 50% van de mannen langer is dan de 84% kortste vrouwelijke patiënten.

Testen

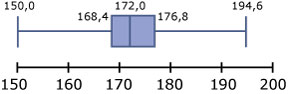15. Hier zie je een boxplot van de lengtes van 1064 vaders van ongeveer 100 jaar geleden.
    1. Welke uitspraak kun je doen over de 25% kortste mannen?
    2. Welke uitspraak kun je doen over de 25% langste mannen?
    3. Hoeveel van deze mannen hadden een lengte vanaf 172,0 tot 176,8 cm?


16. Hier zie je de leeftijdsopbouw van leraren in het HAVO/VWO in procenten.
    
    
    
    
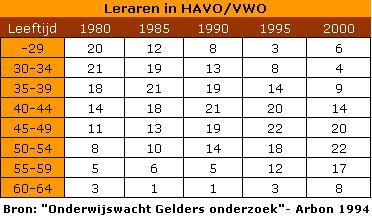
    1. Bereken voor elk van de vijf genoemde jaren het gemiddelde en de standaarddeviatie van de leeftijden van deze leraren.
    2. Teken de vijf frequentiepolygonen en geef daarin die waarden aan.
    3. Welke conclusies kun je trekken?
    4. De waarden van 1995 en 2000 zijn schattingen die de onderzoekers in 1994 hebben gedaan. Passen die schattingen bij de gegevens uit de voorgaande jaren?


17. Open het Excel bestand met de titel "Etmaaltemperaturen De Bilt". Je vindt het in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen

    1. Maak een histogram van de temperaturen in de maand juli over de jaren 1755 tot 1900. Neem een klassenbreedte van 1°C.
    2. Maak ook een histogram voor de periode van 1900 tot 2007.
    3. Vergelijk de twee histogrammen met elkaar. Kun je hieruit concluderen dat de temperatuur in de maand juli na 1900 gemiddeld hoger is dan in de voorgaande periode?