
Gegevens samenvatten
Inleiding
Grote verzamelingen statistische gegevens zijn (ondanks het gebruik van tabellen en diagrammen) vaak nogal onoverzichtelijk. Vergelijken van frequentieverdeling is ook niet altijd in één oogopslag mogelijk.
Daarom worden de resultaten van een statistisch onderzoek vaak samengevat in een aantal getallen die snel informatie geven over frequentieverdelingen, zoals gemiddelden en spreiding van gegevens.
Je leert nu:
- een reeks waarnemingen samen te vatten met centrummaten, zoals gemiddelde, mediaan en modus;
- een reeks waarnemingen samen te vatten met spreidingsmaten, zoals spreidingsbreedte, kwartielafstand en standaardafwijking;
- een reeks waarnemingen samen te vatten in een boxplot.
Je kunt al:
- gegevens in een frequentietabel (zowel met absolute als relatieve als cumulatieve frequenties) verwerken;
- een (cumulatief) histogram en een (cumulatief) frequentiepolygoon maken bij een frequentietabel.
Verkennen
De schoolleiding en de ouderraad willen een goed beeld van de aanwezigheid van
leerlingen in jullie leerjaar bij de diverse vakken. Ze willen dat in een beknopt en helder
verslag van maximaal twee A4'tjes.
Hoe kan zoín beknopt verslag eruit zien zodat iedereen goed geïnformeerd wordt?
Uitleg
Je hebt weer eens een toets gehad. Je leraar doet de mededeling: "De toets was goed gemaakt, het gemiddelde van de klas was 7,3". Word je blij of hoor je liever dat het modale cijfer 7,3 is? Of dat de mediaan 7,3 is?
Met zo'n mededeling probeert iemand een frequentieverdeling met één getal te karakteriseren:
- Het modale cijfer is het cijfer dat het vaakst voorkomt. Hier zegt het niet veel, want misschien komt alleen 7,3 twee keer voor en zijn alle andere cijfers veel lager, maar wel verschillend.
- Ook een mediaan (middelste cijfer) van 7,3 zegt niet veel, hoewel je dan zeker weet dat de helft van de cijfers zeker hoger of gelijk aan 7,3 is (en de andere helft is lager).
- Het gemiddelde krijg je door alle cijfers op te tellen en te delen door het totaal aantal leerlingen. Maar ben jij een bovengemiddelde leerling?
Al deze getallen zeggen op zichzelf weinig.
Het wordt al beter als er een mededeling over de spreiding van de cijfers bij komt.
Bijvoorbeeld zo: "Het gemiddelde cijfer is 7,3 en de cijfers hebben een spreiding van 2,2".
Maar dan moet je wel weten wat er onder de 'spreiding' wordt verstaan: het verschil tussen het hoogste en het laagste cijfer bijvoorbeeld is zo'n spreidingsmaat. Maar er bestaan ook andere spreidingsmaten...
‡
Opgaven
-
Bestudeer de Uitleg. In de tabel zie je de cijfers behaald bij een wiskundetoets door twee parallelklassen.
| Cijfers klas A |
| Cijfers klas B |
| 6,7 | 6,4 | 4,9 | 3,8 | 4,0 |
| 4,0 | 6,2 | 4,9 | 3,9 | 5,9 |
| 5,6 | 5,8 | 6,8 | 8,2 | 4,7 |
| 7,3 | 4,7 | 6,7 | 7,6 | 9,4 |
| 3,4 | 8,5 | 4,1 | 6,9 | 7,3 |
| 8,3 | 5,7 | 7,2 | 8,7 | 7,1 |
| 6,1 | 7,5 | 6,7 | 6,2 | 3,4 |
| 7,0 | 6,5 | 7,4 | 5,0 | 4,8 |
| 7,9 | 4,5 | 8,3 |
|
|
| 7,7 | 6,5 | 4,9 | 8,8 | 6,3 |
-
Waarom heeft het geen zin om van beide klassen het modale cijfer te vergelijken?
-
Bepaal van beide klassen de mediaan.
-
Zegt de mediaan iets over welke klas beter heeft gescoord voor de toets?
-
Bereken van beide klassen het gemiddelde cijfer.
-
Welke van beide klassen heeft het hoogste gemiddelde? Kun je nu zonder meer zeggen dat die klas ook beter heeft gescoord?
-
Je zier hier de SE-cijfers van enkele leerlingen aan het eind van HAVO 5.
Hun eindcijfer SE is het gemiddelde van deze cijfers.

-
Neem aan dat elk SE-cijfer even zwaar meetelt voor het eindcijfer. Welk eindcijfer krijgt elke leerling?
-
De laatste drie cijfers zijn behaald in de vijfde klas. Deze tellen twee keer zo zwaar als de cijfers behaald in klas 4.
Wat wordt nu het gemiddelde cijfer van elke leerling?
Ga er in de rest van deze opgave van uit dat alle SE-cijfers even zwaar meetellen.
In de onderstaande figuur is voor elke leerling elk SE-cijfer aangegeven door een bolletje op een getallenlijn (de komma in het cijfer is weggelaten).
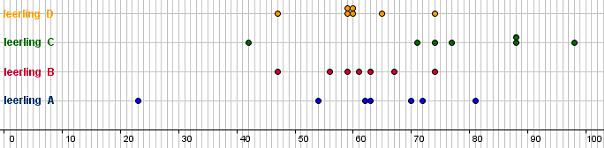
-
De leerlingen A en B hebben hetzelfde gemiddelde. Toch is hun cijferbeeld nogal verschillend. Hoe komt dat?
-
De spreiding van de cijfers van A en C is vrijwel hetzelfde. Waarin verschilt hun cijferbeeld vooral?
-
De leerlingen B en D hebben dezelfde variatiebreedte. Zou je de spreiding van hun cijfers ook hetzelfde willen noemen?
Een andere maat voor de spreiding kun je vinden door te kijken hoe ver elk cijfer van het gemiddelde afligt. Je doet dit door van elk cijfer het verschil met het gemiddelde te berekenen. Hier zie je die verschillen voor leerling A.

-
Bereken het gemiddelde van deze verschillen. Verbaast het antwoord je? Leg uit waarom.
-
Het gemiddelde van deze verschillen is geen goede spreidingsmaat. Dat zit hem in de mintekens.
Door te kwadrateren vallen die mintekens weg. Maak voor leerling A zelf een lijst van de kwadraten van de verschillen.
Bereken daarvan het gemiddelde. Heb je nu een goede spreidingsmaat?
-
Door het kwadrateren wordt het getal dat je zojuist bij d hebt gevonden nogal groot.
Dat los je op door de wortel uit dit getal te nemen. Je krijgt dan de standaardafwijking van deze set cijfers.
Ga na dat voor leerling A die standaardafwijking ongeveer 1,73 is.
-
Bereken ook voor leerling B de verschillen van de cijfers met het gemiddelde.
Bereken vervolgens het gemiddelde van de kwadraten van die verschillen en de standaardafwijking.
-
Bereken de standaardafwijking van de cijfers van leerling D.
Vind je verschillende standaardafwijkingen voor de leerlingen B en D?
Theorie
Getallen die zoín beetje het 'midden' aangeven van een reeks waarnemingen heten centrummaten.
Er zijn drie centrummaten:
- De modus: de waarneming met de hoogste frequentie.
- De mediaan: het middelste waarnemingsgetal. Om de mediaan te bepalen zet je eerst de waarnemingsgetallen
in volgorde van klein naar groot. Is het aantal oneven dan is er echt een middelste. Is het aantal even dan zijn er twee middelste waarnemingsgetallen. De mediaan is het gemiddelde van die middelste twee.
- Het gemiddelde bereken je door alle waarnemingsgetallen op te tellen en te delen door het totaal aantal.
Als je de waarnemingsgetallen x1, x2, ... ,xn noemt, dan schrijf je dit als .
Daarin geldt . De Griekse hoofdletter sigma is het somteken.
Bij een frequentietabel vermenigvuldig je elk waarnemingsgetal met de frequentie.
Het gemiddelde is dan .
Bij klassenindelingen spreek je van de modale klasse en kun je de mediaan het beste opzoeken in een cumulatief relatief frequentiepolygoon (de waarde bij 50% schatten door aflezen). Het gemiddelde kun je dan alleen maar schatten door het gemiddelde van de klassenmiddens te berekenen.
Centrummaten alleen zeggen nog weinig, er hoort steeds een spreidingsmaat bij...
Er zijn drie spreidingsmaten:
- De spreidingsbreedte (ook wel variatiebreedte) is het verschil tussen hoogste en laagste waarnemingsgetal.
- De kwartielafstand is het verschil tussen de mediaan van de grootste helft (het derde kwartiel) en de mediaan van de kleinste helft (eerste kwartiel). Om de kwartielen te bepalen zet je eerst de waarnemingsgetallen
in volgorde van klein naar groot en verdeel je ze in twee helften. Is het aantal oneven dan hoort de mediaan bij beide helften, anders tel je de mediaan niet mee. Vervolgens bepaal je van beide helften weer de mediaan.
- De standaardafwijking (of standaarddeviatie) vind je door van elk waarnemingsgetal het verschil met het gemiddelde te bepalen en dat getal te kwadrateren. Al die kwadraten tel je op en je deelt ze door het totaal aantal waarnemingen. Dit getal heet de variantie. De wortel uit de variantie is de standaarddeviatie: .
De Griekse (kleine) letter sigma is het teken voor standaardafwijking.
Bij klassenindelingen is de spreidingsbreedte het aantal klassen maal de klassenbreedte. De mediaan en de kwartielen zoek je dan het beste op in een cumulatief relatief frequentiepolygoon (de mediaan bij 50%, het eerste kwartiel bij 25% en het tweede kwartiel bij 75%). Het standaarddeviatie kun je dan alleen maar schatten door de standaarddeviatie van de klassenmiddens te berekenen.
‡
Voorbeeld 1
Dit is een steelblad diagram van de cijfers in een klas: tegelijk is het een klassenindeling (eerste klasse 2,0 – <3,0) en een overzicht van alle cijfers.
- De modus is 8,6 en de modale klasse is 6,0 – <7,0.
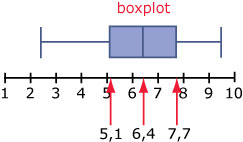
- De mediaan is 6,4 (het gemiddelde van de twee middelste), het eerste kwartiel is 5,1 en het derde kwartiel is 7,7.
- De spreidingsbreedte is 9,5 – 2,4 = 7,1 als je naar de werkelijke cijfers,
of 10,0 – 2,0 = 8,0 als je naar de klassenindeling kijkt.
- De kwartielafstand is 7,7 – 5,1 = 2,6.
Het is de breedte van de box van de boxplot.
| 2 |
| 4 |
| 3 |
| 9 | 9 |
| 4 |
| 4 | 4 |
| 5 |
| 0 | 0 | 1 | 5 | 5 | 9 | 9 |
| 6 |
| 2 | 4 | 4 | 4 | 6 | 6 | 8 | 9 |
| 7 |
| 1 | 3 | 7 |
| 8 |
| 2 | 5 | 6 | 6 | 6 | 6 |
| 9 |
| 5 |
‡
Voorbeeld 2
Hier zie je leeftijd, lengte en gewicht van 36 mannen.
Bepaal van alle drie de series waarnemingsgetallen zowel de drie centrummaten als de drie spreidingsmaten.
Doe dit zowel met de basisgegevens als met de klassenindelingen.
Maak alleen gebruik van de rekenfuncties van Excel maar nog niet van de statistische functies (zie practicum).
Antwoord
Voor de modus en de mediaan zijn de sorteerfuncties van Excel erg handig.
Verder kun je gemakkelijk optellen en kolommen met de waarden van een waarnemingsgetal maal zijn frequentie, enzovoorts, maken.
In deze tweede versie van het Excel-bestand vind je de antwoorden.
Bekijk goed welke formules zijn gebruikt.
Bij de klassenindelingen is telkens niet de mediaan, de kwartielen en de kwartielafstand bepaald, dat gaat beter vanuit een cumulatief relatief frequentiepolygoon, zie voorbeeld 3.
‡
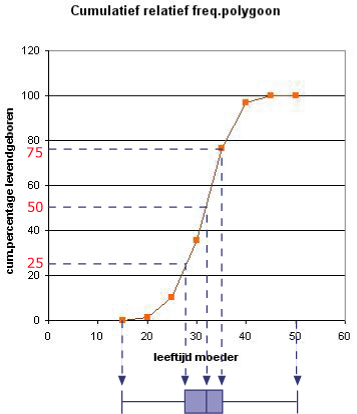
Voorbeeld 3
Hier zie je een cumulatief relatief frequentiepolygoon bij deze klassenindeling van levendgeborenen naar leeftijd van de moeder.
Maak met behulp hiervan een bijpassend boxplot.
Antwoord
Lees bij 50% de mediaan af, bij 25% het eerste kwartiel en bij 75% het derde kwartiel.
Minimum en maximum zitten bij 0% en 100%.
Je ziet:
- het eerste kwartiel is: Q1 ≈ 28
- de mediaan is: Q2 ≈ 31,5
- het derde kwartiel is: Q3 ≈ 35
‡
Opgaven
-
Bekijk Voorbeeld 1.
Maak van beide klassen in opgave 1 een steelblad diagram en bepaal de mediaan en de kwartielafstand van beide klassen.
Teken voor beide klassen een boxplot van de resultaten.
-
Welke uitspraak is waar voor de bovenstaande waarnemingsgetallen?
58 63 51 56 86 69
55 76 74 69 45 75
55 68 68 52 70 57
65 78 65 72 83 65
79
- De modus en mediaan zijn gelijk.
- De modus en het gemiddelde zijn gelijk.
- Het gemiddelde en de mediaan zijn gelijk.
-
Welke uitspraak is waar voor de bovenstaande waarnemingsgetallen?
58 63 51 56 86 69
55 76 74 69 45 75
55 68 68 52 70 57
65 78 65 72 83 65
79 57 63 63 72 63
- De modus is groter dan de mediaan.
- Het gemiddelde is groter dan de mediaan.
- De modus is kleiner dan het gemiddelde.
-
Bekijk Voorbeeld 2.
Je werkt daar met de leeftijd, de lengte en het gewicht van 36 mannen. Als je de tabel in het antwoord opent, kun je daar zien hoe de centrummaten en de spreidingsmaten worden berekend (klik op de juiste cellen en bekijk de formules). Bekijk eerst de "Basisgegevens".
-
Hoe wordt het gemiddelde berekend?
-
Hoe wordt de spreidingsbreedte (variatiebreedte) berekend?
-
Hoe wordt de kwartielafstand berekend?
-
Ga na, dat de modale leeftijd, de modale lengte en het modale gewicht correct zijn.
(Gebruik eventueel de sorteerfunctie in Excel.)
-
Controleer zo ook de mediaan en de kwartielen.
Teken de bijpassende boxplots.
-
Hoe wordt de standaardafwijking berekend?
Ga nu in het Excel-bestand naar "Tabel lengte". Daar wordt gewerkt met een klassenindeling.
Het werken met klassenindelingen is handig als je niet met een computer werkt die grote databestanden aankan.
-
Welke klassenbreedte wordt gebruikt?
-
Hoe wordt nu het gemiddelde berekend?
-
Hoe wordt nu de standaardafwijking berekend?
Hoe kan het dat die standaardafwijking niet hetzelfde is als die van de basisgegevens?
-
Bekijk ook "Tabel leeftijd". Ga na dat daar op dezelfde manier wordt gerekend.
Alleen worden de klassenmiddens anders bepaald. Verklaar dat.
-
De gegevens over leeftijd, lengte en gewicht van 36 vrouwen zijn te vinden via
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
- Bepaal nu vanuit de basisgegevens de centrummaten van de leeftijden, de lengtes en de gewichten.
- Bepaal ook de bijbehorende spreidingsmaten.
- Teken de bijbehorende boxplots.
Vergelijk ze met die van de 36 mannen uit de vorige opgave en beschrijf de verschillen.
- Maak van de lengtes van de 36 vrouwen een geschikte klassenindeling en bereken daarmee benaderingen van het gemiddelde en de standaardafwijking.
-
In twee ziekenhuizen heeft men de keuze uit verschillende maten voor de bedden. Van alle verschillende bedden zijn er evenveel.
Ziekenhuis A: 200 cm, 180 cm, 160 cm, 150 cm, 140 cm
Ziekenhuis B: 220 cm, 180 cm, 160 cm, 150 cm, 120 cm
-
Bereken voor elk ziekenhuis het gemiddelde en de mediaan van de lengtes van de bedden.
-
Geven deze centrummaten het verschil tussen beide ziekenhuizen voldoende aan, wat de maten van de bedden betreft?
Breng dit verschil onder woorden.
-
Op twee plaatsen op aarde heeft men in een bepaalde periode de neerslag gemeten.
Plaats A: 20 mm, 40 mm, 80 mm, 100 mm
Plaats B: 50 mm, 55 mm, 65 mm, 70 mm
-
Reken na dat ze dezelfde mediaan en hetzelfde gemiddelde hebben.
-
Welke plaats heeft de grootste spreiding in neerslag?
-
Geeft de variatiebreedte bij deze twee plaatsen een goede indruk van de spreiding?
-
Bestudeer in Voorbeeld 3 hoe je bij een klassenindeling een boxplot maakt.
Neem nu de gegevens van de 36 mannen uit Voorbeeld 2.
Maak bij de klassenindeling van "Tabel lengte" een cumulatief relatief frequentiepolygoon en print deze figuur. Teken vervolgens een passend boxplot bij deze lengteverdeling.
Practicum
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Samenvatten > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Samenvatten > Practicum
In het practicum kun je leren hoe je de verschillende centrummaten en spreidingsmaten met je GR bepaalt. Erg handig is dit niet, je kunt meestal beter met Excel werken.
Verwerken
-
Gegeven de waarnemingsgetallen 16, 18, 22, 24, 26, 26, 28, 30 en 36.
- Teken er een boxplot bij.
- Doe dat nog eens als je bij alle getallen 4 optelt.
- En ook als je van alle getallen 40 aftrekt.
- Doe het nog eens als je alle getallen door 2 deelt.
- Welk resultaat krijg je als je alle getallen met 3 vermenigvuldigt?
- Beschrijf wat er gebeurt met het boxplot als bij alle waarnemingsgetallen een getal wordt opgeteld of ervan af getrokken wordt.
- Geef een beschrijving van wat er gebeurt met het boxplot als alle waarnemingsgetallen met een getal worden vermenigvuldigd of door een getal worden gedeeld.
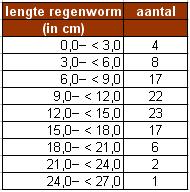 Voor een practicum biologie wordt een aantal regenwormen gevangen. De lengte van die regenwormen vind je in de tabel hiernaast.
Voor een practicum biologie wordt een aantal regenwormen gevangen. De lengte van die regenwormen vind je in de tabel hiernaast.
- Kijk naar de manier waarop de klassen zijn gemaakt.
Hoe nauwkeurig zijn de regenwormen gemeten?
Bij welke klasse hoort een regenworm die 3,0 cm lang is?
- Welke klasse is de modale klasse?
- Teken hierbij een histogram van de cumulatieve relatieve frequenties.
Teken in dezelfde figuur de cumulatieve frequentiepolygoon.
- In welke klasse zit de mediaan? Kun je precies zeggen hoe groot die mediaan is?
Schat de mediaan met behulp van de cumulatieve frequentiepolygoon.
- Bereken het gemiddelde en de standaardafwijking.
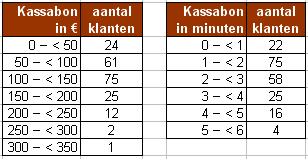 Een supermarkt laat onderzoek verrichten naar de besteding per klant en naar de hoeveel tijd die een klant aan de kassa nodig heeft om af te rekenen. Er worden op verschillende tijdstippen tellingen gehouden. Hier zie je de resultaten.
Een supermarkt laat onderzoek verrichten naar de besteding per klant en naar de hoeveel tijd die een klant aan de kassa nodig heeft om af te rekenen. Er worden op verschillende tijdstippen tellingen gehouden. Hier zie je de resultaten.
- Bepaal bij beide tabellen de modus, de mediaan, het eerste en het derde kwartiel en het gemiddelde.
- Hoe groot is de standaardafwijking bij beide verdelingen?
- Teken bij beide tabellen een boxplot.
De supermarkt heeft een weekomzet van € 150000,-. Een caissiŤre mag 38 uur per week werken.
- Hoeveel caissiŤres moet de supermarkt in dienst nemen als er vanwege de wisselende winkeldrukte een overcapaciteit van 25% wordt aangehouden?
-
Elk uur van een dag is de temperatuur bepaald.

-
Verwerk deze gegevens in een dubbel steelblad diagram.
-
Maak boxplots van elk dagdeel afzonderlijk en van de totale dag.
-
Bereken voor beide dagdelen afzonderlijk het gemiddelde en de standaardafwijking.
-
Bereken het gemiddelde en de standaardafwijking van alle metingen van die dag.
-
Geef een verklaring voor de verschillen die je vindt.
-
In een nieuw te bouwen ziekenhuis moeten bedden worden aangeschaft. De facilitaire dienst vraagt zich af welke lengte de bedden moeten krijgen. Hoe langer de bedden, hoe hoger de kosten. In het oude ziekenhuis hebben ze het laatste jaar van 278 patiŽnten gegevens verzameld. Je vindt ze bij
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
-
Bereken de gemiddelde lengte van de patiŽnten.
Bereken ook de gemiddelde lengte van de vrouwelijke en de mannelijke patiŽnten apart.
-
Men kan natuurlijk alle bedden zo lang maken als de langste patiŽnt.
Hoe lang worden de bedden dan? Noem een bezwaar tegen dit idee.
Handiger is misschien de lengte van het bed zo te kiezen dat 50% van de patiŽnten erin past. Voor langere patiŽnten neem je dan een bed met een lengte van de langste patiŽnt.
-
Hoe lang moet het bed dan worden als 50% van de patiŽnten erin past?
Het hoofd van de facilitaire dienst denkt dat het goedkoper is om verschil te maken in mannen en vrouwenbedden, wat de lengte betreft.
-
Als we hiervan uitgaan en de voorwaarde na b, hoe lang worden dan een "mannenbed" en een "vrouwenbed"?
-
Er wordt beweerd dat het de laatste jaren steeds warmer wordt. Om dit te onderzoeken nemen we de maandtemperaturen van het KNMI. Je vindt ze bij
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
-
Zoek uit hoe het KNMI de temperatuur per maand berekent.
-
Toon met een berekening aan dat het jaar 2006 warmer is dan het jaar 1986.
De gemiddelde wintertemperatuur van 1988 is het gemiddelde van de temperaturen van de maanden december 1987, januari 1988 en februari 1988.
-
Op dezelfde manier kun je de gemiddelde wintertemperatuur van 2003 uitrekenen.
Was de winter van 1988 kouder of warmer dan die van 2003?
-
Het gemiddelde van de getallen `7, 3, 9, 13, 17` en het getal `p` is gelijk aan `9`. Bereken `p`.
-
In klas H4A zitten 20 leerlingen. Voor een toets Engels scoorde de klas gemiddeld 6,6. Ook klas H4B maakte die toets, maar hier was het gemiddelde cijfer 8,1. Het gemiddelde cijfer van de twee klassen samen was 7,5.
-
Leg uit hoe het kan dat het gemiddelde niet gelijk is aan `(6,6+8,1)/2 = 7,35`.
-
Stel het aantal leerlingen in klas H4B gelijk aan `x`. Leg uit dat geldt: `(132 + 8,1x)/(20 + x) = 7,5`.
-
Hoeveel leerlingen zitten er in klas H4B?
-
De jongens in klas H4A scoorden gemiddeld 6,4 en de meisjes 6,9. Hoeveel jongens zitten er in klas H4A?
-
Een boer heeft 120 melkkoeien, bestaande uit roodbonte en zwartbonte koeien. De gemiddelde melkproductie per koe is 22 liter per dag. De zwartbonte koeien hebben een gemiddelde melkproductie van 24 liter per dag en de roodbonte hebben een gemiddelde dagproductie van 21,55 liter. Hoeveel zwartbonte koeien heeft de boer?
-
Men neemt aan dat de leerlingen van groep 8 van de basisscholen in Nederland elk jaar ongeveer even goed presteren op de Cito-toets. Het is moeilijk om elk jaar een toets te maken die even moeilijk is als die van het jaar daarvoor.
Een leerling die een moeilijke toets maakt zal dan slechter scoren dan een even slimme leerling, die een gemakkelijke toets gemaakt heeft. Daarom vergelijkt men de resultaten op een toets met die van alle andere kinderen in datzelfde jaar. Jouw score is dan het percentage van alle leerlingen die slechter gepresteerd hebben dan jij. Deze score noemt men percentielscore.
Voorbeeld: Je krijgt een percentielscore van 80 als 80% van de Nederlandse leerlingen lager haalde dan jij.
-
Leg uit dat twee leerlingen uit verschillende klassen met hetzelfde aantal punten voor dezelfde toets verschillende percentielscores kunnen hebben.
-
Waarom is het niet eerlijk als jouw leraar deze becijfering in de klas zou toepassen?
-
Welke centrummaat is gelijk aan een percentielscore van 50?
-
Kunnen alle leerlingen van een school een hogere score hebben dan 80?
Omdat een score van 0 zo frustrerend is heeft men de Cito-scores opgeschaald: minimum = 500, maximum = 550. Om toegelaten te worden tot het HAVO hanteren veel scholen de grens van 537 punten.
-
Welke percentielscore hoort hierbij?
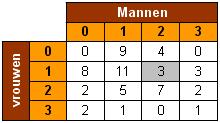 Van de huishoudens in de Bernhardlaan zijn het aantal mannelijke en vrouwelijke personen geteld. De gegevens staan in deze tabel.
De 3 in het gearceerde vakje geeft aan dat er drie huishoudens zijn met twee mannelijke personen en met ťťn vrouwelijk persoon.
Van de huishoudens in de Bernhardlaan zijn het aantal mannelijke en vrouwelijke personen geteld. De gegevens staan in deze tabel.
De 3 in het gearceerde vakje geeft aan dat er drie huishoudens zijn met twee mannelijke personen en met ťťn vrouwelijk persoon.
-
Bereken het gemiddelde aantal personen per huishouden in ťťn decimaal nauwkeurig.
-
De gemiddelde leeftijd van de mannen is 26,0 jaar en van de vrouwen is dat 18,2 jaar.
Bereken in ťťn decimaal nauwkeurig de gemiddelde leeftijd van de gehele groep.
-
Het aantal mannen in de Bernhardlaan neemt met twee toe. De een is vijf jaar ouder dan de ander.
De gemiddelde leeftijd van de mannen neemt met ťťn jaar toe tot 27,0 jaar. Hoe oud zijn de nieuwkomers?
-
Ga weer uit van de situatie in de tabel. Tien huishoudens verlaten de Bernhardlaan.
Van de overblijvende huishoudens bereken je het gemiddelde aantal personen.
Bereken in ťťn decimaal nauwkeurig de kleinste waarde die dit gemiddelde kan aannemen.
Testen
-
Op een feestje zijn 8 personen aanwezig. Hier zie je een tabel met gegevens over de feestgangers.
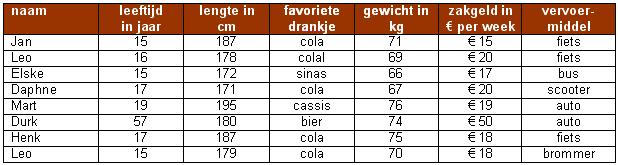
- Welke centrummaat zou je gebruiken om voor elke kolom de feestgangers te typeren?
- Welke spreidingsmaat (indien mogelijk) zou je gebruiken om voor elke kolom de feestgangers te typeren?
- Hoe kun je nu de "doorsnee" feestganger omschrijven?
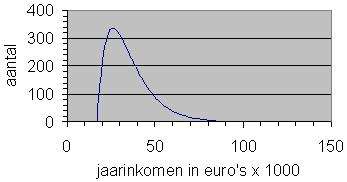 In de grafiek vind je de jaarinkomens van de werknemers van een grote fabriek.
In de grafiek vind je de jaarinkomens van de werknemers van een grote fabriek.
-
Wat verdient de doorsnee werknemer van deze fabriek?
Welke centrummaat heb je gekozen en waarom?
-
Welke centrummaat is hier groter, de mediaan of de modus? Leg uit waar je dat aan kunt zien.
-
Een groep leerlingen wordt tijdens de muziekles gevraagd op hun instrument te blazen en een bepaalde toon zo lang mogelijk vast te houden. De tijd dat dit lukt wordt genoteerd in seconden:
20 35 21 19 23 25 21 19 36 42
31 29 26 27 26 29 32 25 20 18
23 25 26 22 28 20 35 34 21
-
Bepaal de modus, de mediaan en het gemiddelde van deze gegevens.
-
Bepaal de spreidingsbreedte en de standaardafwijking.
-
Teken een boxplot bij deze gegevens.
-
Maak een klassenindeling, waarbij de eerste klasse `15 - < 20` is.
-
Bereken het gemiddelde en de standaarddeviatie bij deze klassenindeling.
-
Teken een bijpassend cumulatief relatief frequentiepolygoon. Bepaal daarmee de mediaan bij deze klassenindeling.






 Voor een practicum biologie wordt een aantal regenwormen gevangen. De lengte van die regenwormen vind je in de tabel hiernaast.
Voor een practicum biologie wordt een aantal regenwormen gevangen. De lengte van die regenwormen vind je in de tabel hiernaast.
 Een supermarkt laat onderzoek verrichten naar de besteding per klant en naar de hoeveel tijd die een klant aan de kassa nodig heeft om af te rekenen. Er worden op verschillende tijdstippen tellingen gehouden. Hier zie je de resultaten.
Een supermarkt laat onderzoek verrichten naar de besteding per klant en naar de hoeveel tijd die een klant aan de kassa nodig heeft om af te rekenen. Er worden op verschillende tijdstippen tellingen gehouden. Hier zie je de resultaten.

 Van de huishoudens in de Bernhardlaan zijn het aantal mannelijke en vrouwelijke personen geteld. De gegevens staan in deze tabel.
De 3 in het gearceerde vakje geeft aan dat er drie huishoudens zijn met twee mannelijke personen en met ťťn vrouwelijk persoon.
Van de huishoudens in de Bernhardlaan zijn het aantal mannelijke en vrouwelijke personen geteld. De gegevens staan in deze tabel.
De 3 in het gearceerde vakje geeft aan dat er drie huishoudens zijn met twee mannelijke personen en met ťťn vrouwelijk persoon.

 In de grafiek vind je de jaarinkomens van de werknemers van een grote fabriek.
In de grafiek vind je de jaarinkomens van de werknemers van een grote fabriek.