
Diagrammen gebruiken
Inleiding
Nadat de gegevens geordend zijn in een tabel, wil je deze ook grafisch verwerken.
Een figuur is vaak gemakkelijker te lezen en toegankelijker voor de lezer.
Maar welk type diagram kun je nu het beste gebruiken?
Het begrip diagram is een zeer algemeen begrip, er is dus heel veel keuze...
Je leert nu:
- verschillende soorten diagrammen te tekenen: staafdiagram, histogram, cirkeldiagram, steel-bladdiagram, lijndiagram, frequentiepolygoon, cumulatief frequentiepolygoon;
- een keuze te maken uit de genoemde diagrammen om je onderzoekgegevens te verwerken.
Je kunt al:
- gegevens in een frequentietabel (zowel met absolute als relatieve frequenties) verwerken;
- staafdiagrammen, lijndiagrammen en cirkeldiagrammen maken bij gegevens.
Verkennen
Zoek op internet naar afbeeldingen van diagrammen. Mogelijke zoekwoorden zijn: diagram, graph (voor Engelstalige sites).
Geef bij elk diagram aan welk verhaal het vertelt; je vindt daar vaak informatie over in de kop van het betreffende artikel.
Uitleg
Een diagram is een grafische voorstelling van gegevens.
(In Engelstalige landen spreek je van een 'chart', of een 'graph'. Het Engelse 'diagram' is meer wat wij een graaf noemen.
Handig om te weten bij zoeken op internet!)
Diagrammen kunnen er op heel veel manieren uitzien.
De belangrijkste zijn:
- beelddiagram of pictogram (Engels: pictogram)
- staafdiagram (Engels: bar graph)
- lijndiagram (Engels: line graph)
- cirkeldiagram (Engels: pie graph)
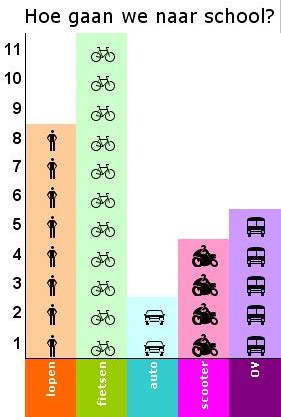
Dit beelddiagram laat zien met welk vervoermiddel de leerlingen in een klas naar school komen.
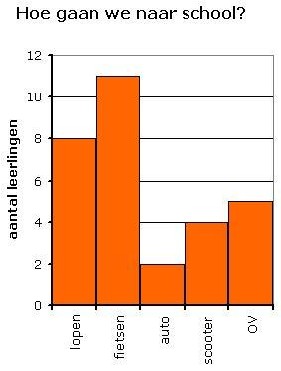
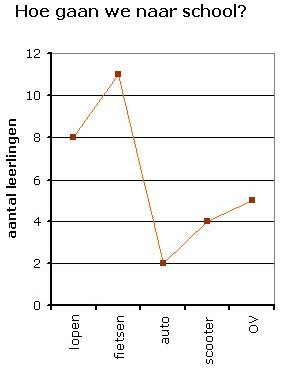
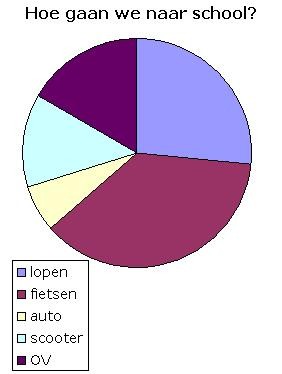
Ditzelfde kan worden weergegeven in een staafdiagram, een lijndiagram en een cirkeldiagram.
Bij een cirkeldiagram moet je alle aantallen omrekenen naar een sectorhoek.
Dat doe je door de relatieve frequentie te vermenigvuldigen met 360°.
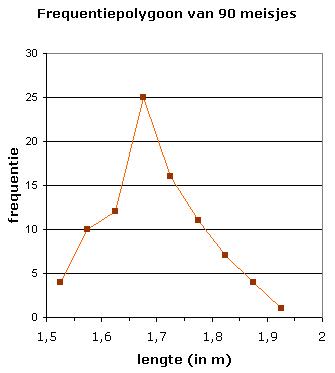 Een histogram is een bijzonder soort staafdiagram.
In een histogram zet je kwantitatieve variabelen met een oplopende volgorde, b.v. de hoeveelheid boterhammen (1, 2, 3, etc.) die leerlingen mee naar school nemen, de lengtes van de meisjes uit 4-vwo, maar niet de manieren waarop je naar school gaat.
Een histogram is een bijzonder soort staafdiagram.
In een histogram zet je kwantitatieve variabelen met een oplopende volgorde, b.v. de hoeveelheid boterhammen (1, 2, 3, etc.) die leerlingen mee naar school nemen, de lengtes van de meisjes uit 4-vwo, maar niet de manieren waarop je naar school gaat.
Bij een klassenindeling zet je de klassengrenzen links en rechts van de staaf. Gebruik je geen klassen dan staan de waarnemingsgetallen midden onder de staven. En je zet de staven tegen elkaar met een vaste klassenbreedte.
De hoogte van de staven geeft de (relatieve) frequentie (van de waarneming) aan.
Een frequentiepolygoon ontstaat door in een histogram de middens van de bovenkanten van de staven te verbinden. Zoals het histogram een bijzonder soort staafdiagram is, is het frequentiepolygoon een bijzonder soort lijndiagram.
Je kunt ook een histogram van de somfrequenties maken in plaats van de frequenties.
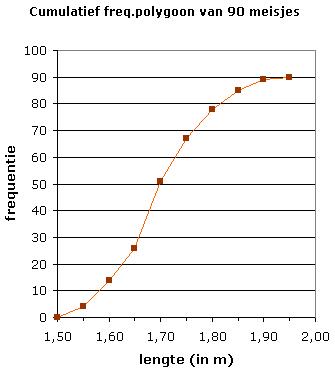
Verbind je de rechterbovenkanten van de staven dan ontstaat een cumulatief frequentiepolygoon
(of somfrequentiepolygoon of kleiner-gelijk-kromme).
 ‡
‡
Opgaven
-
Bestudeer de Uitleg.
Bekijk de vier verschillende soorten diagrammen over de manier waarop in een bepaalde klas de leerlingen naar school gaan.
-
Maak vanuit het beelddiagram een frequentietabel.
-
Maak bij de frequentietabel een kolom met relatieve frequenties.
-
Maak een staafdiagram en een lijndiagram met relatieve frequenties.
-
Laat zien hoe je de sectorhoeken van het cirkeldiagram berekent.
-
Welk voordeel hebben relatieve frequenties boven absolute frequenties?
-
Houd zelf zon onderzoekje over de manier van naar school gaan in je klas.
-
Hier zie je een frequentiepolygoon met daarin de lengtes van 90 meisjes.
-
Welke klassenindeling is er gebruikt?
-
Hoe kun je deze frequentiepolygoon omzetten naar een histogram?
-
Hoe maak je een cumulatieve frequentiepolygoon?
De gegevens van de 90 meisjes zijn terug te vinden via
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen
-
Maak zelf een frequentiepolygoon.
-
Maak zelf een cumulatief histogram.
Theorie
Een eenvoudige manier om waarnemingen in beeld te brengen, is een staafdiagram.
Bij een staafdiagram hoeft de horizontale as geen logische volgorde te hebben. Verbind je de middens van de bovenkanten van de staven van een staafdiagram door lijnstukjes dan krijg je een lijndiagram.
Een histogram is een staafdiagram waar op de horizontale as getallen met een logisch oplopende volgorde moeten staan.
Verbind je de middens van de bovenkanten van de staven van een histogram met lijntjes dan krijg je een frequentiepolygoon.
Een cirkeldiagram laat in een oogopslag zien welke waarnemingen naar verhouding vaker voorkomen dan andere.
Van de cumulatieve frequenties bij een verdeling kun je ook een histogram en een frequentiepolygoon tekenen.
Zon polygoon heet een cumulatief frequentiepolygoon.
Je verbindt hierbij de meetpunten boven de rechtergrenzen van de klassen.
Het steelbladdiagram is een variant op de frequentietabel.
Eigenlijk is het een frequentietabel en een histogram tegelijk, waarbij ook nog de afzonderlijke waarnemingen zichtbaar blijven.
‡
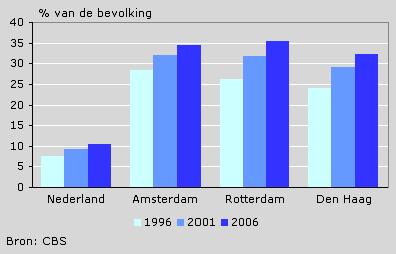
Voorbeeld 1
De bovenste figuur is een staafdiagram.
Je kunt de steden (met de bijbehorende drie staven) onderling rustig verwisselen.
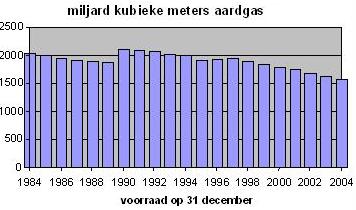
De onderste figuur is een histogram.
Nu vertonen de getallen op de horizontale as een nette oplopende volgorde.
Verwisselen van die getallen mag niet.
Het was netter geweest als ook de staven de juiste klassenbreedte hadden gekregen.
‡
Voorbeeld 2
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Diagrammen > Voorbeeld 1
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Diagrammen > Voorbeeld 1
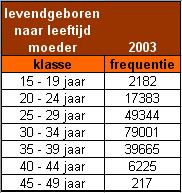
Maak een histogram en een frequentiepolygoon van relatieve frequenties bij deze klassenindeling van levendgeborenen naar leeftijd van de moeder die je op de website vindt.
Antwoord
Maak eerst de lijst met relatieve frequenties.
In Excel gaat dat heel gemakkelijk:
- Sla eerst het XL-bestand op je eigen PC op.
- Tel in cel B10 de inhoud van de cellen B3 t/m B9 op.
- Gebruik in cel C3 een formule als =$B3/$B$10*100 en kopieer die naar de cellen er onder (C4 t/m C9).
Maak vervolgens het histogram en het frequentiepolygoon.
In deze nieuwe versie van de klassenindeling van levendgeborenen naar leeftijd van de moeder zie je het resultaat.
Merk op dat Excel eigenlijk geen histogram kan tekenen.
Je maakt een staafdiagram dat zoveel mogelijk op een echt histogram lijkt.
(Op de horizontale as komt namelijk geen normale schaalverdeling, maar de namen van de klassen.)
‡
Voorbeeld 3
Maak een cumulatief relatief frequentiepolygoon bij deze klassenindeling van levendgeborenen naar leeftijd van de moeder.
Antwoord
Maak eerst de lijst met relatieve frequenties en van cumulatieve relatieve frequenties.
In Excel gaat dat heel gemakkelijk, zie voorbeeld 2.
Maak vervolgens een lijst met rechterklassengrenzen.
Nu ga je geen lijndiagram maken, maar je kiest voor "Spreiding" en je maakt een lijngrafiek.
In deze nieuwe versie van de klassenindeling van levendgeborenen naar leeftijd van de moeder zie je het resultaat.
Merk op dat Excel geen cumulatief histogram kan tekenen en eigenlijk ook geen cumulatief frequentiepolygoon.
Je maakt een grafiek die zoveel mogelijk op een echt frequentiepolygoon lijkt.
‡
Opgaven
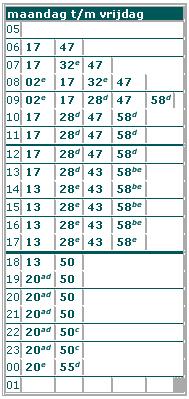 Dit is een deel van de dienstregeling van een busdienst. Het is een steelblad diagram.
Dit is een deel van de dienstregeling van een busdienst. Het is een steelblad diagram.
-
Schrijf per heel uur de frequentie op in een frequentietabel.
-
Maak een histogram met het aantal busritten per uur.
-
Welke informatie heb je wel in een steelblad diagram en niet in een histogram?
-
Welke informatie staat zowel in een steelblad diagram als in een histogram?
-
Waarom maak je bij elk onderzoek niet altijd een steelblad diagram in plaats van een histogram?
-
Bekijk Voorbeeld 1.
- Wat is het verschil tussen een histogram en een staafdiagram?
- Wat is het voordeel van een histogram boven een staafdiagram?
- Wat is er niet netjes aan het getekende histogram?
- Wat is het verschil tussen een frequentiepolygoon en een lijndiagram?
-
Bekijk Voorbeeld 2. Maak zelf in Excel het histogram en de polygoon van relatieve frequenties bij deze klassenindeling van levendgeborenen naar leeftijd van de moeder.
-
Bekijk Voorbeeld 3. Maak zelf in Excel het histogram en de polygoon van cumulatieve relatieve frequenties bij deze klassenindeling van levendgeborenen naar leeftijd van de moeder.
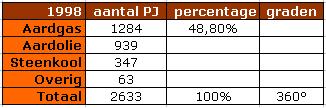 Hier zie je gegevens over het verbruik van energie in 1998.
Hierin is het verbruik gegeven in PJ (1 PJ = 1 PetaJoule = `10^(15)` Joule).
Hier zie je gegevens over het verbruik van energie in 1998.
Hierin is het verbruik gegeven in PJ (1 PJ = 1 PetaJoule = `10^(15)` Joule).
- Bereken de procentuele verhoudingen tussen Aardgas, Aardolie, Steenkool en Overige in 1988.
- Maak een cirkeldiagram voor het energieverbruik in het jaar 1988.
In deze tabel zie je het verbruik in PJ in de loop van de jaren.
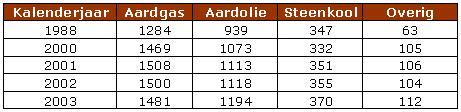
- Teken een nieuw cirkeldiagram voor de onderlinge verhoudingen tussen Aardgas, Aardolie, Steenkool en Overig voor het jaar 2003 met behulp van deze tabel.
- Vergelijk de procentuele verhouding tussen Aardgas, Aardolie, Steenkool en Overig van de jaren 1988 en 2003. Wat valt je op?
Practicum
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Diagrammen > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Diagrammen > Practicum
In het practicum kun je leren hoe je diagrammen met je grafische rekenmachine maakt. Erg handig is dit niet, je kunt meestal beter met Excel werken.
Verwerken
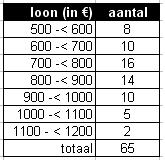 Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
- Bereken de relatieve frequenties bij deze tabel.
- Maak een staafdiagram van de frequenties en van de relatieve frequenties.
- Maak ook een bijpassende frequentiepolygoon.
Het bedrijf neemt vijf extra werknemers in dienst. Zij krijgen een weekloon van € 835,=, € 1156,=, € 1345,=, € 1567,= en € 1714,=.
- Pas de frequentietabel aan voor deze 70 werknemers.
- Teken een staafdiagram en een lijndiagram bij de nieuwe frequentietabel.
- Teken een relatieve frequentiepolygoon van de 70 werknemers met een klassenbreedte van 200.
-
Voor een bepaalde toets kun je maximaal 100 punten scoren.
Hier zie je hoe een groep van 40 personen de toets heeft gemaakt.
Scores:
59 57 53 60 63 58 77 33 50 59
58 75 62 54 53 78 59 68 65 62
57 60 80 47 90 30 60 35 57 87
63 65 63 58 65 70 73 58 63 55
- Deel deze scores in klassen in, neem als laagste klasse `25 -< 35`. Maak een frequentietabel.
- Maak bij deze tabel een histogram van relatieve frequenties.
- Maak ook een frequentiepolygoon met de relatieve frequenties.
- Personen die 55 of meer punten hebben behaald, scoren voldoende. Hoeveel procent van deze groep scoorde voldoende?
-
In de tabel zie je de cijfers behaald bij een wiskundetoets door twee parallelklassen.
| Cijfers klas A |
| Cijfers klas B |
| 6,7 | 6,4 | 4,9 | 3,8 | 4,0 |
| 4,0 | 6,2 | 4,9 | 3,9 | 5,9 |
| 5,6 | 5,8 | 6,8 | 8,2 | 4,7 |
| 7,3 | 4,7 | 6,7 | 7,6 | 9,4 |
| 3,4 | 8,5 | 4,1 | 6,9 | 7,3 |
| 8,3 | 5,7 | 7,2 | 8,7 | 7,1 |
| 6,1 | 7,5 | 6,7 | 6,2 | 3,4 |
| 7,0 | 6,5 | 7,4 | 5,0 | 4,8 |
| 7,9 | 4,5 | 8,3 |
|
|
| 7,7 | 6,5 | 4,9 | 8,8 | 6,3 |
- Verwerk de resultaten van beide klassen in ιιn frequentietabel en teken het bijbehorende histogram. Kies een klassenbreedte van 0,5.
Om te laten zien hoe de toets gemaakt is kunnen de resultaten ook verwerkt worden in een steelblad diagram.
- Maak zo'n steelblad diagram.
Om het verschil tussen beide klassen te onderzoeken worden de resultaten verwerkt in een dubbel steelblad diagram.
- Maak dit dubbele steelblad diagram.
- Noem enkele voordelen die het steelblad diagram heeft boven een frequentietabel en een histogram.
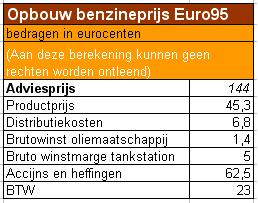 Hier zie je de opbouw van de benzineprijs van Euro95 volgens de Bovag.
Hier zie je de opbouw van de benzineprijs van Euro95 volgens de Bovag.
-
Hoeveel procent is volgens de Bovag bruto winstmarge voor het tankstation?
-
Geef de opbouw weer in een cirkeldiagram.
-
Wat zal de Bovag een consument vertellen die klaagt over de hoge benzineprijzen?
-
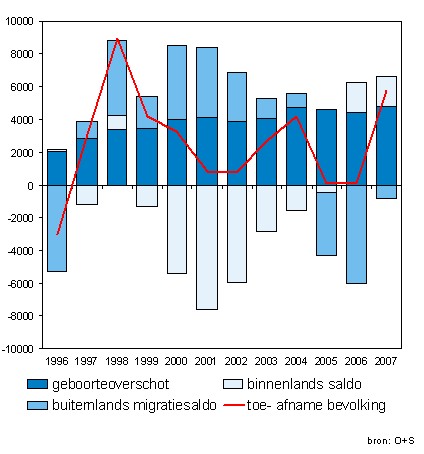
Deze figuur geeft informatie over de bevolking van Amsterdam.
-
Welke soorten diagrammen tref je in de figuur aan?
-
Wat betekenen de variabelen geboorteoverschot, buitenlands migratiesaldo en binnenlands saldo?
-
Hoeveel bedraagt de bevolkingstoename van Amsterdam in 2004 ongeveer?
Hoeveel zijn in dat jaar het geboorteoverschot, het buitenlands migratiesaldo en het binnenlands saldo?
-
Het migratiesaldo zit de ιne keer boven en de andere keer onder de nullijn. Geef daar een verklaring voor.
-
Aan het lijndiagram zie je dat in 2007 de Amsterdamse bevolking met ongeveer 6000 personen is toegenomen.
Laat zien hoe je dit kunt berekenen vanuit het staafdiagram.
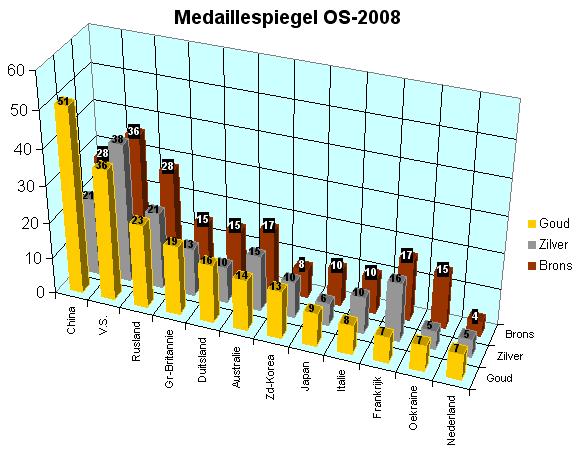
 Onder deze opgave zie je de medaillespiegel van de Olympische Spelen van 2008 in Beijng, alleen de beste 12 landen.
Onder deze opgave zie je de medaillespiegel van de Olympische Spelen van 2008 in Beijng, alleen de beste 12 landen.
-
Wat geeft elke staaf in dit diagram weer?
-
Waarom is een 3D-diagram hier handig? Wat staat er op elk van de assen weergegeven?
-
Welk land heeft de meeste gouden medailles gewonnen?
-
Welk land won de meeste zilveren medailles?
-
Welk land heeft in totaal de meeste medailles gewonnen?
-
Deze gegevens kun je ook in een gestapeld staafdiagram weergeven.
Hoe komt het er dan uit te zien? Wat is daarvan het voordeel? En wat is het nadeel?
-
Kun je nog een andere wijze van presentatie bedenken die alle gewenste informatie bevat en toch een duidelijk overzicht geeft?
-
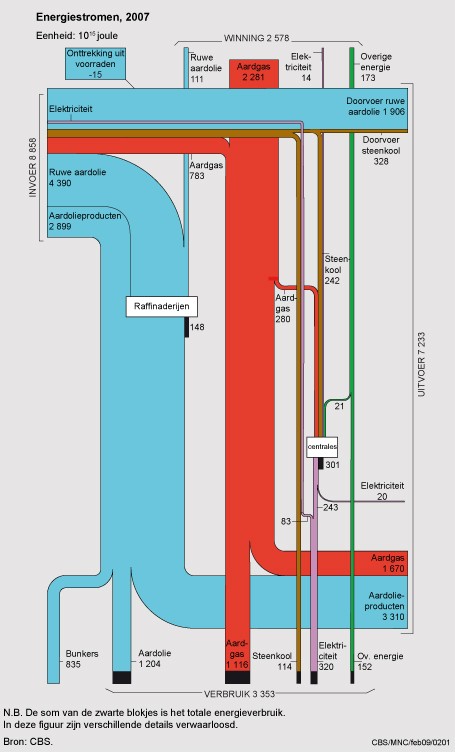
Dit stroomdiagram stelt de energiebalans van Nederland voor. Je vindt er de hoeveelheid energie die Nederland zelf opwekt en invoert. Je vindt er ook de energie die we met zn allen verbruiken dan wel doorvoeren/uitvoeren naar het buitenland. De gebruikte eenheid is `10^(15)` joule.
-
Wat betekent het getal 2281 bij de Aardgaswinning?
-
Hoeveel joule aan energie is er in 2007 verbruikt door onze energiecentrales om elektriciteit op te wekken?
-
Deze energiecentrales halen hun energie behalve uit aardgas en steenkool ook uit andere energiebronnen.
Waaruit blijkt dat? En om welke energiebronnen zou dat gaan?
-
Hoeveel joule aan energie is er in Nederland in 2007 verbruikt?
-
Hoeveel joule aan energie is er in Nederland in 2007 ingevoerd?
-
Hoeveel joule aan energie is er als elektriciteit ingevoerd?
-
Waarom was het vinden van aardgas in de Nederlandse bodem de afgelopen jaren zo belangrijk voor onze economie?
-
Nederland kent ook opgeslagen energievoorraden. Je ziet dat in het schema op twee plaatsen. Waar?
Testen
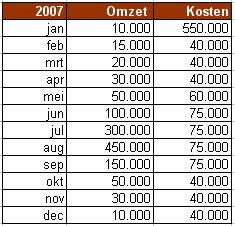 Hier zie je de omzet en de kosten van een bedrijf. Beide staan vermeld in euros en afgerond op veelvouden van 5.000.
Hier zie je de omzet en de kosten van een bedrijf. Beide staan vermeld in euros en afgerond op veelvouden van 5.000.
- Teken de cumulatieve frequentiepolygoon van de omzet en van de kosten in ιιn figuur. Nummer de maanden 1 t/m 12.
- In welke maanden ligt de cumulatieve frequentiepolygoon van de kosten boven die van de omzet?
- Wat betekent dit voor het bedrijf?
- Wat is het eindresultaat voor dit bedrijf over het gehele jaar?
-
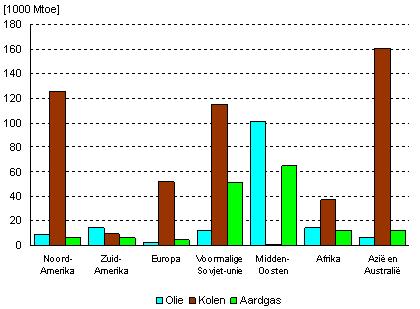
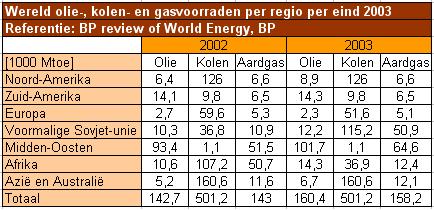
Je ziet hieronder een staafdiagram van de wereld olie-, kolen- en gasvoorraad per regio per eind 2003. (Bron: http://www.energie.nl).
Ook zie je de bijbehorende data voor eind 2003 en eind 2002.
Mtoe = Miljoen ton olie-equivalenten = 41 808 TeraJoules.
-
Hoe kun je zien dat dit diagram geen histogram is?
-
Waarom is een staafdiagram gemaakt en geen cirkeldiagram, denk je?
-
Maak een cirkeldiagram voor de aardgasvoorraad per regio per eind 2003.
-
Welk soort diagram zou je maken als je de voorraden per regio per eind 2003 en per eind 2002 met elkaar wilt vergelijken?
Teken dit diagram.
 Een histogram is een bijzonder soort staafdiagram.
In een histogram zet je kwantitatieve variabelen met een oplopende volgorde, b.v. de hoeveelheid boterhammen (1, 2, 3, etc.) die leerlingen mee naar school nemen, de lengtes van de meisjes uit 4-vwo, maar niet de manieren waarop je naar school gaat.
Een histogram is een bijzonder soort staafdiagram.
In een histogram zet je kwantitatieve variabelen met een oplopende volgorde, b.v. de hoeveelheid boterhammen (1, 2, 3, etc.) die leerlingen mee naar school nemen, de lengtes van de meisjes uit 4-vwo, maar niet de manieren waarop je naar school gaat.




 ‡
‡



 Dit is een deel van de dienstregeling van een busdienst. Het is een steelblad diagram.
Dit is een deel van de dienstregeling van een busdienst. Het is een steelblad diagram.
 Hier zie je gegevens over het verbruik van energie in 1998.
Hierin is het verbruik gegeven in PJ (1 PJ = 1 PetaJoule = `10^(15)` Joule).
Hier zie je gegevens over het verbruik van energie in 1998.
Hierin is het verbruik gegeven in PJ (1 PJ = 1 PetaJoule = `10^(15)` Joule).

 Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
 Hier zie je de opbouw van de benzineprijs van Euro95 volgens de Bovag.
Hier zie je de opbouw van de benzineprijs van Euro95 volgens de Bovag.

 Onder deze opgave zie je de medaillespiegel van de Olympische Spelen van 2008 in Beijng, alleen de beste 12 landen.
Onder deze opgave zie je de medaillespiegel van de Olympische Spelen van 2008 in Beijng, alleen de beste 12 landen.


 Hier zie je de omzet en de kosten van een bedrijf. Beide staan vermeld in euros en afgerond op veelvouden van 5.000.
Hier zie je de omzet en de kosten van een bedrijf. Beide staan vermeld in euros en afgerond op veelvouden van 5.000.

