
Verzamelen en ordenen

Inleiding
Een onderzoek levert heel veel vragenlijsten op of heel veel waarnemingen en metingen.
Je zult eerst overzicht moet krijgen over al die gegevens.
Je moet ze netjes ordenen.
Dat doe je vaak door eerst te "turven" hoeveel je van elke categorie hebt.
Je leert nu:
- de ruwe gegevens uit een onderzoek te ordenen in een overzichtelijke tabel;
- bij veel verschillende gegevens een klassenindeling te maken;
- de begrippen turftabel, frequentietabel en somfrequentietabel;
- de begrippen klassenbreedte en klassengrens;
- het onderscheid tussen frequentie en relatieve frequentie.
Je kunt al:
- een turftabel maken;
- rekenen met procenten.
Verkennen
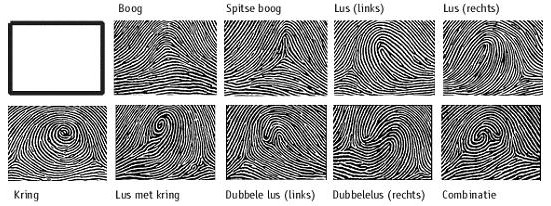
Sir Francis Galton heeft rond 1890 vingerafdrukken bestudeerd.
Hij ontdekte dat je bij vingerafdrukken grofweg drie patronen kunt onderscheiden:
de boog, de kring en de lus.
Deze indeling is vrij globaal. Voor sommige patronen moeten ook nog het aantal lijnen tussen de kern en delta geteld worden. Hierdoor is ieder mens te identificeren op grond van de vingerafdruk.
(Voor meer informatie, zie www.vingerafdrukken.nl over dactyloscopie.)
- Hoe zou je gegevens over vingerafdrukken van bijvoorbeeld alle leerlingen kunnen verzamelen, ordenen en snel kunnen terugvinden in een bestand?
Uitleg
Na een onderzoek heb je meestal veel gegevens. Je zult moeten sorteren en samenvatten.
Het maken van een turftabel is een goede manier om een overzicht te krijgen.
In een turftabel begin je met het opschrijven van de lijst met mogelijke waarnemingen.
Naast elke mogelijke waarneming geef je met streepjes ("turven") aan hoe vaak hij voor komt.
Op het eind vervang je die streepjes door het aantal, de absolute frequentie. Je krijgt dan een
frequentietabel, met een frequentieverdeling.
Deel je de frequentie door het totaal aantal waarnemingen dan vind je de fractie
van die waarneming. De fractie kun je ook uitdrukken in een percentage.
In beide gevallen spreek je van de relatieve frequentie.
Hier zie je hoe van de drie hoofdcategorieën vingerafdrukken een frequentietabel kan worden gemaakt.
| linker duimafdruk |
aantal |
abs.freq. |
fractie |
rel.freq. |
| lus | ||||| ||| | 8 | `8/25 = 0,32`
| 32% |
| boog | ||||| ||||| | | 11 | `11/25 = 0,44`
| 44% |
| kring | ||||| | | 6 | `6/25 = 0,24`
| 24% |
Vaak heb je met veel verschillende waarnemingen te maken. Veel ervan hebben frequentie 1.
Je maakt dan een klassenindeling.
Zorg dat je ongeveer 10 klassen krijgt om mee te werken.
Is het kleinste meisje `1,51` m is en het langste `1,98` m, kun je klassen maken met een
klassenbreedte van 5 centimeter. De klassen sluiten altijd op elkaar aan.
De eerste klasse is dan `1,50 - < 1,55`.
De tweede klasse is dan `1,55 - < 1,60`.
Enzovoorts...
De notatie –< betekent "vanaf... tot...".
De waarden 1,50 en 1,55 van de eerste klasse worden de klassengrenzen genoemd.
Een meisje dat precies 1,55 m lang is zit in de tweede klasse, want die begint bij 1,55.
Tip 1: Neem voor het aantal klassen minimaal 5 en maximaal 20.
Je maakt het aantal ongeveer gelijk aan de wortel uit het aantal waarnemingsgetallen.
Tip 2: Voor de klassenbreedte neem je het verschil tussen de grootste en de kleinste waarneming en dat deel je door het aantal klassen. Vaak rond je af op een heel getal.
Het noteren van klassen gebeurt ook wel anders.
Wordt een indeling in aantallen bijvoorbeeld gestart met 15 – 16 en de tweede is 17 – 18, dan spreken je van de "vanaf... tot en met..." notatie.
De klassengrenzen zijn hier 14,5, 16,5 en 18,5. De klassenbreedte is 2.
Voor continue kwantitatieve variabelen gebruik je vaak de "vanaf... tot..." notatie.
Voor discrete kwantitatieve variabelen gebruik je vaak de "vanaf ... tot en met..." notatie.
‡
Opgaven
-
Bestudeer de Uitleg, pagina 1.
Bij het onderzoeken naar welke soort vingerafdrukken er in een klas voorkomen is alleen onderscheid gemaakt tussen "lus", "boog" en "kring"?
-
Welke mogelijkheid is er nog meer als je alle varianten van de "lus" buiten beschouwing laat? Zie Verkennen.
Kennelijk kwam die mogelijkheid in deze klas niet voor.
-
Welke fractie hoort er bij de "lus"?
-
Welk voordeel hebben relatieve frequenties boven absolute frequenties?
-
Houd zelf zon vingerafdrukken onderzoekje in je klas.
 Bekijk nu de Uitleg, pagina 2.
Bekijk nu de Uitleg, pagina 2.
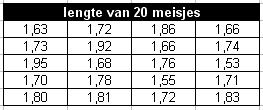
Hier zie je een tabel met daarin de lengtes van 20 meisjes.
-
Maak hierbij een frequentietabel met een klassenindeling. Je eerste klasse is `1,50 -< 1,55`.
-
Reken in de frequentietabel alle absolute frequenties om naar relatieve frequenties.
-
Maak zon relatieve frequentietabel voor de lengtes van alle leerlingen in je klas. Welke klassengrenzen kies je?
Theorie
De absolute frequentie is het aantal keren dat een waarneming voorkomt.
Het bijhouden van het aantal keren dat een waarneming voorkomt, gebeurt vaak in een turftabel. Een frequentietabel is het overzicht van het aantal keren dat alle waarnemingen voorkomen. Je noemt dit wel een frequentieverdeling.
De fractie is de frequentie van een waarneming gedeeld door het totaal aantal waarnemingen.
Je spreekt dan ook wel van de relatieve frequentie.
Bij een frequentietabel kun je een somfrequentietabel maken door bij elke frequentie de voorafgaande frequenties op te tellen. Zo maak je ook een relatieve somfrequentietabel.
Somfrequenties noem je ook wel cumulatieve frequenties ("cumuleren" betekent "opstapelen").
Heb je veel verschillende waarnemingsgetallen dan werk je met een klassenindeling.
Klassen kun je op twee manieren noteren:
-
vanaf... tot...: 1,50 –< 1,60
-
vanaf... tot en met...: 10 – 14 (dit komt overeen met 9,5 –< 14,5)
Voor continue kwantitatieve variabelen gebruik je de eerste notatie.
Voor discrete kwantitatieve variabelen gebruik je de tweede notatie.
(Voor leeftijden is de zaak nog iets lastiger: 10 – 14 betekent dan 10 –< 15.)
De klassengrenzen zijn de onderste en bovenste waarnemingen van een klasse.
Het verschil tussen twee opvolgende klassengrenzen is de klassenbreedte.
‡
Voorbeeld 1
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Ordenen > Voorbeeld 1
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Ordenen > Voorbeeld 1
Op de website vind je in deze tabel in Excel de schoenmaat van 75 mensen op zaterdag 14 juli 2007 in de schoenenwinkel van v.O. in H.
Maak zelf een complete frequentieverdeling door de bijbehorende kolommen met absolute frequenties en die met relatieve frequenties te maken. Maak ook een cumulatieve frequentietabel en een cumulatieve relatieve frequentietabel.
Antwoord
Het is verstandig om eerst het XL-bestand op de eigen pc op te slaan en er dan pas in te gaan werken!
In deze tweede tabel in Excel vind je de absolute frequenties en de relatieve frequenties. Ga na, hoe je Excel gebruikt om het rekenwerk voor je te doen. (Als je op een cel klikt kun je zien welke formule er wordt gebruikt om de inhoud van die cel te berekenen.)
In deze derde tabel in Excel vind je de cumulatieve frequenties en de cumulatieve relatieve frequenties.
‡
Voorbeeld 2
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Ordenen > Voorbeeld 2
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Ordenen > Voorbeeld 2
Op de website vind je in deze tabel in Excel de lengtemaat van 90 meisjes weer. (Als je ermee wilt werken sla dan dit bestand eerst op je eigen PC op.)
Maak een klassenindeling met een klassenbreedte van 5 cm en als ondergrens 1,50 m.
Antwoord
Maak in het Excel-bestand eerst de klassenindeling.
En turf dan de aantallen, maak een (absolute) frequentietabel.
(Excel kan automatisch turven in series getallen, in het practicum "Statistiek rond lengte en gewicht (1)" kun je zien hoe dat in zijn werk gaat.)
Let er op dat de eerste klasse 1,50 –< 1,55 is, en de tweede klasse 1,55 –< 1,60, enzovoorts...
In deze tweede tabel in Excel vind je de absolute frequenties en de relatieve frequenties.
‡
Voorbeeld 3
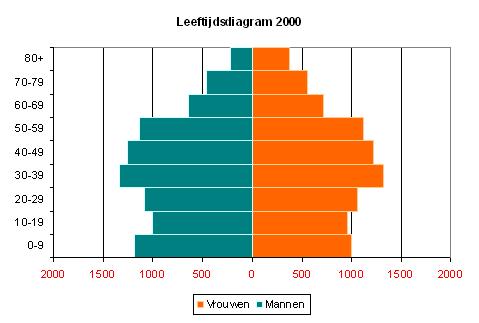
In dit leeftijdsdiagram van de Nederlandse bevolking in 2000 zie je hoe de klassenindeling 0 – 9, 10 – 19, 20 – 29, etc., wordt gebruikt. De aantallen Nederlanders zijn duizendtallen.
De klasse 10 – 19 bijvoorbeeld bevat de Nederlandse mannen of vrouwen die een leeftijd hebben vanaf 10 tot en met 19 jaar. Die klasse loopt van 10 tot 20 jaar: 10 –< 20.
Opgaven
-
Bekijk Voorbeeld 1. Om met de tabel te kunnen werken klik je met de rechter muisknop op de tabel in Excel en kies je "Doel opslaan als". Zo sla je het Excel-bestand eerst op je eigen pc op. Als je het vervolgens opent kun je er in werken.
-
Maak eerst zelf een frequentietabel en een relatieve frequentietabel.
Voeg daar vervolgens een cumulatieve frequentietabel en een cumulatieve relatieve frequentietabel aan toe.
-
Open nu het antwoord en bekijk de derde tabel in Excel. Heb je bij a zelf ook zon tabel gemaakt?
-
Voeg bij de absolute frequenties één waarneming 36 toe. Hoeveel getallen veranderen er in de frequentietabel?
-
Hoeveel getallen veranderen er in de somfrequentietabel?
-
Hoeveel getallen veranderen er in de relatieve somfrequentietabel?
-
Bekijk nog eens Voorbeeld 1.
- Haal bij de absolute frequenties één waarneming 44 weg. Hoeveel getallen veranderen er in de frequentietabel?
- Hoeveel getallen veranderen er in de somfrequentietabel?
- Hoeveel getallen veranderen er in de relatieve somfrequentietabel?
-
Bekijk Voorbeeld 2. Voer eerst zelf de opdracht uit en controleer je antwoord.
- Verander de klassenbreedte van 5 in 8. Wat is nu de hoogste frequentie?
- Verander de klassenbreedte van 5 in 2. Wat is nu de hoogste frequentie?
- Probeer nog een aantal klassenbreedten. Welke klassenbreedte is volgens jou het meest geschikt?
-
Bekijk Voorbeeld 3. Je ziet een leeftijdsdiagram van de Nederlandse bevolking in 2000.
- Welke klassengrenzen heeft de klasse 0 9?
- Als je het aantal klassen van 9 in 3 verandert, wat is dan de hoogste frequentie?
- Waarom is het verhogen van het aantal klassen nu niet mogelijk zonder extra informatie?
-
Is dit juist of onjuist?
- In een relatieve frequentietabel of relatieve somfrequentietabel staan altijd percentages.
- De totale relatieve somfrequentie is in theorie altijd 100%.
- De totale relatieve somfrequentie is in de praktijk altijd 100%.
- De relatieve frequentie is overal 100%.
- De relatieve frequenties zijn behalve bij de laatste klasse altijd lager dan 100%.
Verwerken
 Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
Je ziet de frequentieverdeling van de weeklonen van 65 werknemers van een bedrijf.
- Geef de ondergrens van de zesde klasse.
- Geef de bovengrens van de vierde klasse.
- Geef het klassenmidden van de derde klasse.
- Welke ondergrens en welke bovengrens heeft de vijfde klasse?
- Welke klassenbreedte is hier gebruikt?
-
Voor een bepaalde toets kun je maximaal 100 punten scoren.
Hier zie je hoe een groep van 40 personen de toets heeft gemaakt.
Scores:
59 57 53 60 63 58 77 33 50 59
58 75 62 54 53 78 59 68 65 62
57 60 80 47 90 30 60 35 57 87
63 65 63 58 65 70 73 58 63 55
- Deel deze scores in klassen in, neem als laagste klasse `25 -< 35`. Maak een frequentietabel.
- Maak bij deze tabel een kolom van relatieve frequenties.
-
Genereer in Excel of met je GR 100 toevalsgetallen van 1 t/m 20.
- Maak een turftabel.
- Maak een frequentietabel.
- Maak een tabel met relatieve frequenties en somfrequenties.
- Welke relatieve frequenties verwacht je bij de 20 getallen als je een 1.000.000 toevalsgetallen van 1 t/m 20 zou genereren?
-
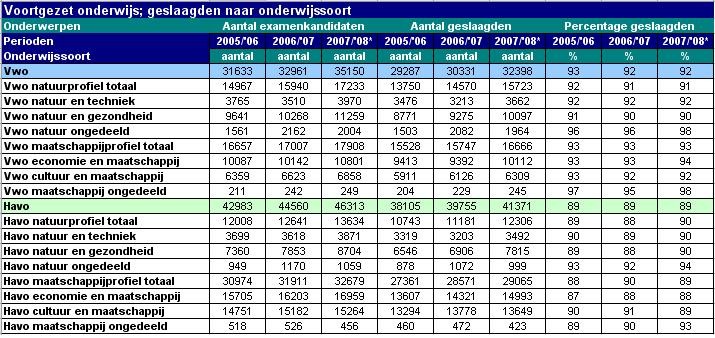
Deze tabel laat het aantal geslaagden zien op havo en vwo gedurende een drietal schooljaren. (Bron: C.B.S. juli 2009)
-
Om welke populatie gaat het bij deze data?
-
Welke variabelen worden er onderzocht? Welke soort variabele betreft het?
-
Waar vind je absolute frequenties en waar relatieve frequenties?
-
Op het Havo is in 2007/2008 het geslaagdenpercentage 89. Toon dit aan door een berekening.
-
Hoeveel procent van de examenkandidaten Havo heeft in 2007/2008 een N-profiel gekozen?
En hoeveel M-profielers zijn er dat jaar op Havo?
-
Kun je het geslaagdenpercentage Havo in 2007/2008 berekenen vanuit de percentages geslaagden van de M-profielen en de N-profielen afzonderlijk?
-
Het aantal examenkandidaten met een N-profiel op Havo neemt absoluut gezien toe. Is dat relatief bekeken ook zo?
-
Kun je verklaren waarom de examenkandidaten in alle ongedeelde N-profielen of M-profielen een hoger geslaagdenpercentage hebben dan het totaal per profiel?
-
Onder 48 medewerkers en studenten van de Vrije Universiteit Brussel heeft enkele jaren geleden een onderzoek naar racisme plaatsgevonden. Er werden 53 vragen gesteld. Hier vind je de vragenlijst en de resultaten.
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen > Datasets
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek > Totaalbeeld > Toepassingen > Datasets
Verwerk deze ruwe gegevens zo handig mogelijk in een overzichtelijke tabel.
Gebruik het getal RG als maat voor de mate van racisme:
`RG = v1+v2+v3-v4-v5+v6+v7+v8-v9-v10+v11-v12+v13-v14+v15+v16-v17+ +v18-v19+v20-v21+v22+v23-v24-v25-v26+v27-v28-v29-v30+v31+v32+v33+ +v34+v35+v36-v37+v38+v39+v40+v41+v42+v43-v44-v45+v46+v47+v48+ +v49 +v50+v51+v52-v53+19*4`.
Testen
-
Van de leerlingen in een brugklas is gevraagd hun schoenmaat op te schrijven.
Schoenmaat
40 42 37 38 40
35 41 36 38 37
38 40 40 40 39
40 39 38 41 40
41 39 39 39 34
41 37 38 45 42
- Maak een frequentietabel en een tabel met relatieve frequenties.
- Maak ook een cumulatieve relatieve frequentietabel van de schoenmaten.
- Hoeveel procent van de leerlingen in deze klas heeft een schoenmaat boven de 40?
-
Voor een biologiepracticum moet het aantal slakken op een stuk grond worden geteld. Het stuk grond wordt daartoe in stukken van 1 m2 verdeeld. Iedere leerling telt het aantal slakken op vier van die stukken.
Hier zie je de resultaten:

-
Om welke populatie gaat het hier en om welke variabele? Wat voor soort variabele betreft het?
-
Hoeveel m2 is de oppervlakte van dat stuk grond?
-
Hoeveel leerlingen hebben er geteld?
-
Hoeveel slakken zijn er in totaal geteld?
-
Hoeveel slakken zijn er gemiddeld per m2 gevonden?
 Bekijk nu de Uitleg, pagina 2.
Bekijk nu de Uitleg, pagina 2.




