Kansen optellen en aftrekken

Inleiding

Je hebt nu het vaasmodel en de bijbehorende kansboom leren kennen. Het lijkt een handig instrument om alle kansproblemen op te lossen, maar toch is het in de praktijk niet altijd even bruikbaar. Zodra het om grotere aantallen trekkingen gaat, wordt een kansboom onoverzichtelijk. Bij trekkingen uit een kaartspel bijvoorbeeld is dit al snel het geval. Dan is het handiger om terug te vallen op regels die beschrijven wanneer je kansen moet optellen en wanneer je ze juist moet vermenigvuldigen.
Daarom wordt nu de kansrekening iets exacter opgebouwd: de kansrekening is een stelsel van regels voor het rekenen met kansen.

Je leert nu:

• kansen berekenen met behulp van regels;
• de basisbegrippen en de basisregels van de kansrekening.

Je kunt al:

• kansen bepalen met behulp van een kansboom;
• het vaasmodel met of zonder teruglegging voor het berekenen van kansen.

Verkennen

Een volledig kaartspel kent 52 kaarten, van elke "kleur" evenveel.
Je trekt aselect uit zo'n kaartspel één kaart.

> Bereken de kans op hartenaas.
> Bereken de kans op hartentwaalf.
> Bereken de kans op een hartenkaart.
> Bereken de kans op geen aas.
> Bereken de kans op een hartenkaart of een ruitenkaart.
> Bereken de kans op een hartenkaart of een boer.
> Bereken de kans op een hartenkaart of een plaatje.

Uitleg

Een volledig kaartspel kent 52 kaarten, van elke "kleur" evenveel.
Je trekt aselect uit zo'n kaartspel één kaart.

• De kans op een hartenkaart is:
  P(hartenkaart) = `13/52` want daar zijn er 13 van.
• De kans op hartentwaalf is dan:
  P(hartentwaalf) = 0 want zo'n kaart bestaat niet.
• De kans op geen hartenkaart is:
  P(geen hartenkaart) = `(52-13)/52 = 1 - 13/52`.
• De kans op een hartenkaart of een ruitenkaart is:
  P(harten of ruiten) = `(13+13)/52 = 13/52 + 13/52`.
• De kans op een boer, een aas of een hartenvrouw is:
  P(boer of aas of hartenvrouw) = `(4+4+1)/52 = 4/52 + 4/52 + 1/52 = 9/52`.

Het lijkt er op dat je bij "of" eenvoudigweg de kansen kunt optellen. Maar dat is hier alleen maar zo, omdat de mogelijkheden elkaar wederzijds uitsluiten. Vraag je namelijk naar een hartenkaart of een boer, dan zijn er niet 13 + 4 gunstige mogelijkheden, maar slechts 13 + 4 – 1 vanwege de hartenboer die anders twee keer wordt geteld. "hartenkaart" en "boer" sluiten elkaar niet wederzijds uit.

• De kans op hartenkaart of boer is: P(hartenkaart of boer) = `13/52 + 4/52 - 1/52 = 16/52`.

‡

Opgaven

1. Lees eerst de Uitleg goed door.
   Uit een compleet spel speelkaarten wordt aselect een kaart getrokken.
   1. Wat is de kans dat het een plaatje is?
   2. Wat is de kans dat het geen plaatje is?
   3. Wat is de kans dat het een harten is?
   4. Wat is de kans dat het een harten plaatje is?
   5. Wat is de kans dat het een harten kaart is of een heer?
   6. Waarom kun je bij e niet gewoon de kans op een harten kaart en de kans op een heer optellen?
   7. Wordt de kans op harten of heer kleiner als ruiten heer en harten aas in het spel ontbreken?

Theorie

Bij een bepaald kansexperiment zoals het trekken van een kaart uit een kaartspel bestaat een uitkomstenverzameling met 52 mogelijkheden. Een gebeurtenis zoals "het trekken van een tien" is dan een deel van die uitkomstenverzameling (er zijn 4 tienen). Bij elke gebeurtenis hoort een bepaalde kans. Hierbij gelden de volgende kansregels:

• De kans op een onmogelijke gebeurtenis (niets uit de uitkomstenverzameling) is 0.
• De kans op een zekere gebeurtenis (de complete uitkomstenverzameling) is 1.
• Is G een gebeurtenis, dan is P(G) de kans op die gebeurtenis en `0 < text(P)(G) <= 1`.
• De complementregel:
  Is niet-G de ontkenning van gebeurtenis G dan is P(niet-G) = 1 – P(G).
  Je noemt niet-G en G wel complementaire gebeurtenissen.
• De somregel:
  • als de gebeurtenissen G₁ en G₂ elkaar wederzijds uitsluiten, dan is
    P(G₁ of G₂) = P(G₁) + P(G₂).
  • als de gebeurtenissen G₁ en G₂ elkaar niet wederzijds uitsluiten, dan is
    P(G₁ of G₂) = P(G₁) + P(G₂) – P(G₁ en G₂).

Je ziet dat voor twee gebeurtenissen G₁ en G₂ die elkaar wederzijds uitsluiten geldt:
P(G₁ en G₂) = 0.

‡

Voorbeeld 1

Een volledig kaartspel kent 52 kaarten, van elke "kleur" evenveel.
Je trekt aselect uit zo'n kaartspel één kaart.
Bereken de kans op een hartenkaart of een plaatje.

Antwoord

Er zijn 13 hartenkaarten en 4 · 4 = 16 plaatjes.
Maar deze gebeurtenissen sluiten elkaar niet uit: er zijn 4 hartenplaatjes.

De gevraagde kans is dus: P(hartenkaart of plaatje) = `13/52 + 16/52 - 4/52 = 25/52`.

‡

Voorbeeld 2

Je trekt een lot uit een serie met de nummers 10, 11, 12, ..., 99.
Heb je een 2 of een 3 in het lotnummer, dan heb je een prijsje.
Hoe groot is de kans hierop?

Antwoord

Eerst het cijfer 2:

• de kans op links een 2 is `9/90` en de kans op rechts een 2 is `10/90`

Dus de kans op een 2 is (denk aan 22): `9/90 + 10/90 - 1/90 = 18/90` .

De kans op een 3 in het lotnummer is op dezelfde manier `18/90`.

De kans op een 2 of een 3 in het lotnummer is (denk aan 23 en 32): `18/90 + 18/90 - 2/90 = 34/90`.

‡

Voorbeeld 3

Je mag vier keer met een dobbelsteen gooien tot je een 6 krijgt. Je mag maximaal vier keer proberen.
Hoe groot is de kans dat dit lukt?

Antwoord

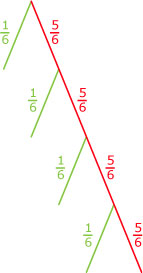
Maak hierbij een kansboom: groen stelt het werpen van een 6 voor en rood stelt geen 6 voor. Zo liggen de kansen:

• meteen een 6 gooien: kans `1/6`;
• pas tweede worp een 6 gooien: kans `5/6 * 1/6`;
• pas derde worp een 6 gooien: kans `(5/6)^2 * 1/6`;
• pas vierde worp een 6 gooien: kans `(5/6)^3 * 1/6`.

Dit kan echter eenvoudiger door vast te stellen dat de complementaire gebeurtenis is: 4 keer achter elkaar geen 6 gooien. Daarbij hoort een kans van `(5/6)^4`.
De gevraagde kans is daarom `1 - (5/6)^4 ~~ 0,52`.

‡

Opgaven

2. Bekijk het kaartspel nog eens, zie ook Voorbeeld 1. Je trekt er aselect één kaart uit. Welke van de volgende gebeurtenissen sluiten elkaar uit?
   1. Harten kaart of schoppen kaart.
   2. Harten kaart of vrouw.
   3. Kaart met even getal of plaatje.
   4. Kaart met even getal of ruiten kaart.


3. Bereken de kansen op de gebeurtenissen in opgave 2.
   


4. Bekijk Voorbeeld 2.
   1. Wat is de kans dat het getrokken briefje het cijfer 0 bevat?
   2. Wat is de kans dat het getrokken briefje het cijfer 0 en het cijfer 2 bevat?
   3. Wat is de kans dat het getrokken briefje het cijfer 0 of het cijfer 2 bevat?
   4. Bereken de kans dat het getrokken briefje geen 0 en ook geen 2 bevat? Maak gebruik van de complementregel.


5. Je gooit met twee gewone dobbelstenen, een rode en een witte. `R` is het aantal ogen op de rode dobbelsteen, `W` dat op de witte.
   1. Maak een overzicht van alle mogelijkheden.
   2. Hoe groot is `text(P)(R=5)`?
   3. Hoe groot is `text(P)(W=4)`?
   4. Hoe groot is `text(P)(R=5` en `W=4)`?
   5. Hoe groot is `text(P)(R=5` of `W=4)`?
   6. Sluiten de gebeurtenissen `R=5` en `W=4` elkaar wederzijds uit?


6. In Voorbeeld 3 gaat het om het werpen met een dobbelsteen tot je een zes gooit. Je mag nu tien keer proberen.
   1. Hoe groot is de kans dat je bij de derde worp voor het eerst een zes gooit?
   2. Hoe groot is de kans dat je bij de achtste worp voor het eerst een zes gooit?
   3. Hoe groot is de kans dat je een zes gooit?
   4. Waarom is nu de complementregel wel erg handig?


7. De raad van commissarissen van een bouwonderneming heeft 11 leden. Daaronder zijn 5 economen en 4 juristen. 2 van de economen zijn ook jurist. De leden zijn om de beurt een maand voorzitter. De volgorde is door loten vastgesteld.
   1. Ga met behulp van een Venndiagram na hoeveel leden econoom noch jurist zijn.
   2. Wat is de kans dat de voorzitter deze maand econoom en jurist is?
   3. Wat is de kans dat de voorzitter deze maand econoom of jurist is?
   4. Wat is de kans dat zowel deze maand als de volgende de voorzitter econoom of jurist is?

Verwerken

8. Van de leerlingen van een groep staat 70% voldoende voor wiskunde, 63% staat voldoende voor natuurkunde en 43% staat voldoende voor beide vakken.
   1. Hoeveel procent staat voldoende voor minstens een van beide vakken?
   2. Hoeveel procent staat onvoldoende voor beide vakken?
   3. Hoeveel procent staat voldoende voor wiskunde en onvoldoende voor natuurkunde?
   4. Hoeveel procent staat voldoende voor wiskunde of onvoldoende voor natuurkunde?


9. Bij een spel moet je eerst kruis of munt gooien. Gooi je kruis, dan moet je met een dobbelsteen gooien, gooi je munt, dan mag je met twee dobbelstenen gooien. Bereken de volgende kansen.
   1. De kans dat je 12 ogen gooit.
   2. De kans dat je 7 ogen gooit.
   3. De kans dat je 7 of 12 ogen gooit.
   4. De kans dat je meer of minder dan 7 ogen gooit.
   5. De kans dat je 6 ogen gooit.


10. Van de leerlingen van een school is 52% meisje, 48% jongen. 1 van elke 13 meisjes draagt een hoofddoek (om religieuze redenen), 1 van elke 16 jongens draagt een basketbalpet (om onbekende redenen).
    1. Hoeveel procent van de leerlingen draagt een hoofddoek? Hoeveel procent een basketbalpet?
    2. Wat is de kans dat een aselect aangewezen leerling een jongen zonder pet is?
    3. Wat is de kans dat een aselect aangewezen leerling een meisje is of iets op het hoofd draagt?
    4. Wat is de kans dat een aselect aangewezen leerling een jongen is of niets op het hoofd draagt?
    5. Wat is de complementaire gebeurtenis van die bij d?


11. Voor de ontwikkeling van kinderen zijn doosjes in de handel gebracht met plastic rondjes, vierkantjes, rechthoekjes en driehoekjes. Van elke soort zijn er grote en kleine stukjes. Van elke soort en elke grootte zijn er twee rode stukjes, twee gele en twee blauwe. Totaal dus 48 stuks. Bereken de kans dat een aselect gekozen stukje:
    1. geel is of een vierkantje;
    2. rood is of geen vierkantje;
    3. klein is of geen vierkantje;
    4. blauw is of geel, of een driehoekje.


12. Een fabrikant van koekjes wil een nieuwe variant op de markt brengen: het "kaakje". Als proef probeert hij drie smaakvarianten die hij I, II en III nummert. Hij vraagt 100 personen om te komen proeven en een oordeel te geven over de smaak van elke variant. De proever geeft met "positief" aan dat hij het kaakje lekker vindt en met "negatief" dat dit niet zo is. Het testresultaat is: 10 proevers vonden alle smaken positief, 8 proevers vonden geen enkele smaak positief. 42 proevers vonden smaak I positief, 49 proevers vonden smaak II positief en 41 proevers vonden smaak III positief. 15 mensen vonden zowel smaak I als smaak II positief, 17 mensen vonden zowel smaak II als smaak III positief.
    1. Hoeveel mensen vonden zowel smaak I als smaak III positief?
    2. Hoeveel proevers vonden smaak I of smaak III positief?
    3. Hoe groot is de kans dat een willekeurige proever smaak I of smaak II of beide positief heeft beoordeeld?

Testen

13. Een spel kaarten om mee te 'toepen' bevat van elk der vier kleuren alleen de kaarten 7, 8, 9, 10, Boer, Vrouw, Heer en Aas. Totaal 32 kaarten. Beantwoord de vragen zowel door tellen van gunstige mogelijkheden als door gebruik van de somregel.
    1. Wat is de kans dat een uit zo'n spel getrokken kaart een ruiten of een plaatje is?
    2. Wat is de kans dat een uit zo'n spel getrokken kaart een harten of een 9 of een 10 is?
    3. Wat is de kans dat een uit zo'n spel getrokken kaart een 9 of een 10 is of geen harten?


14. In een vaas zitten 9 balletjes, 3 rode, 3 blauwe en 3 gele. Ze zijn ook genummerd, van elke kleur draagt één balletje nummer 1, één balletje nummer 2 en één balletje nummer 3. Er wordt aselect een balletje getrokken. Bepaal de kans dat:
    1. het balletje niet rood is;
    2. het balletje rood is of nummer 2 heeft;
    3. het balletje niet blauw is of niet nummer 3 heeft.


15. Een bestuur van 25 personen bestaat uit oprichters, oplichters en opzichters. Sommige leden hebben meer dan één van die kwaliteiten. Er zijn 10 oprichters, 11 oplichters en 15 opzichters. 1 persoon is zowel oprichter als oplichter en opzichter. 3 zijn oprichter en oplichter (en misschien ook opzichter) en 4 zijn oprichter en opzichter (en misschien oplichter).
    1. Maak op grond van deze gegevens een Venndiagram.
    2. Wat is de kans dat een willekeurig bestuurslid keurig is (geen oplichter)?
    3. Wat is de kans dat een willekeurig bestuurslid oprichter is? Dat hij oplichter is? Dat hij beide is?
    4. Bepaal de kans dat een willekeurig bestuurslid oprichter of oplichter is.
    De kans dat een bestuurslid oprichter, oplichter of opzichter is, is natuurlijk 1. Iemand zegt: "Die kans moet de kans zijn dat hij oprichter of oplichter is, plus de kans dat hij opzichter is."
    5. Redeneren helpt niet, dus toon hem dat zijn resultaat niet goed kan zijn en vertel hem dan hoe het wel moet.