Experimenteren

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Experimenteren > Inleiding

Probeer de kansen die bij Verkennen worden beschreven zo goed mogelijk te beredeneren of vermeld waarom er over de kans op de gebeurtenis niets kan worden gezegd.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Experimenteren > Uitleg

Opgaven

1. Lees eerst pagina 1 van de Uitleg goed door.
   1. Waarom is bij het gooien met twee dobbelstenen de kans op 10 ogen kleiner dan die op 7 ogen?
   2. Hoe zou je de kans dat je wiskundeleraar morgen ziek is kunnen vinden?
   3. Hoe zou je de kans kunnen bepalen dat een ouderpaar dat allebei bruine ogen heeft ook een kind met bruine ogen krijgt?
   4. Waarom is de kans dat je met een dobbelsteen een even aantal ogen gooit 50%?
   5. Hoe kom je aan de kans van 80% dat Ajax een bepaalde wedstrijd wint?
   6. Hoezo is de kans op een rood veld bij roulette `18/37`? (Bekijk het plaatje van de roulette.)


2. Ga nu naar pagina 2 van de Uitleg om na te lezen hoe kansen door experimenteren kunnen worden bepaald.
   1. Hoe groot schat je de kans op vier ogen bij het 600 keer werpen met een dobbelsteen?
   2. En hoe groot schat je die kans bij het 6000 keer werpen?
   3. Lijkt de conclusie gerechtvaardigd dat dit een eerlijke dobbelsteen is?


3. Iemand vraagt zich af hoe groot de kans is dat een punaise, als hij valt, met de punt naar boven komt te liggen.
   1. Hoe kun je een benadering krijgen van deze kans? Voer dit ook uit.
   2. Welke experimentele kans heb je gevonden?
   3. Zou je die kans nauwkeuriger kunnen bepalen? Zo ja, hoe dan?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Experimenteren > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

4. In Voorbeeld 1 vind je een dobbelstenensimulator.
   Daarmee kun je het werpen met 1 of met 2 dobbelstenen naspelen zonder echt over dobbelstenen te beschikken.
   1. Stel de simulator eerst in op het werpen met 1 dobbelsteen. Werp 100 keer met 1 dobbelsteen en houd bij hoe vaak je 1, 2, 3, 4, 5, of 6 ogen krijgt. Welke experimentele kans op 6 ogen vind je?
   2. Stel de simulator vervolgens in op het werpen met 2 dobbelstenen. Werp 100 keer met 2 dobbelsteen en houd bij hoe vaak je 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, of 12 ogen krijgt. Welke experimentele kans op 7 ogen vind je?
   3. Is bij jou de experimentele kans op 7 ogen ook groter dan die op 10 ogen?
   4. Kun je beredeneren met de wet van de grote aantallen waarom dit (ook als het bij jou niet klopt) toch het geval is?


5. Met toevalsgetallen op je grafische rekenmachine kun je het werpen met een dobbelsteen simuleren. Daartoe vermenigvuldig je elk toevalsgetal (die liggen immers tussen 0 en 1) met 6 en laat je de cijfers achter de komma weg. Bekijk Voorbeeld 2.
   1. Welke mogelijke getallen krijg je?
   2. Wat moet je doen om de getallen 1 tot en met 6 in beeld te krijgen?
   3. Leg nu uit hoe je het werpen met een dobbelsteen kunt simuleren met je grafische rekenmachine. Bekijk eventueel het bijbehorende practicum via

      www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Experimenteren > Practicum GR

   4. Simuleer 600 worpen met een dobbelsteen en geef de resultaten weer in een staafdiagram.
   5. Hoe groot schat je de experimentele kans op vijf ogen?
   Je kunt ook het werpen met twee dobbelstenen simuleren met de grafische rekenmachine.
   6. Leg uit hoe dat gaat en maak ook nu een staafdiagram van de uitkomsten van 600 worpen met twee dobbelstenen. Hoe groot schat je de experimentele kans op vijf ogen bij het werpen met twee dobbelstenen?


6. Bekijk Voorbeeld 3. Je ziet het staafdiagram met de lengteverdeling van 500 Nederlandse soldaten. De fabrikant van truien voor het leger heeft ook de maten medium (M) voor soldaten vanaf 1,75 m tot en met 1,90 m en large (L) voor soldaten vanaf 1,90 m.
   1. Hoe groot schat je de kans dat een Nederlandse soldaat een trui van maat M nodig heeft?
   2. Hoe groot schat je de kans dat een Nederlandse soldaat een trui van maat L nodig heeft?
   3. De fabrikant bepaald op grond van deze experimentele kansen hoeveel truien van elke maat hij zal maken als er een grote bestelling binnenkomt. Maar hij krijgt te horen dat maat L niet bevalt: voor soldaten van meer dan 2,00 m lengte zijn deze truien te klein. Hij besluit een maat XL in de voeren voor deze soldaten. Hoeveel procent van zijn truien zal hij in maat XL laten produceren?


7. De tabel geeft informatie over het voor komen van kleurenblindheid:
   
   

   	man	vrouw	totaal
   kleurenblind	479	58	573
   niet kleurenblind	5226	4237	9463
   Totaal	5705	4295	10000

   
   
   1. Je komt een man uit deze groep tegen en wilt de kans schatten dat hij kleurenblind is.
      Welk getal beschouw je dan als "aantal herhalingen van het kansexperiment" en welk getal als "aantal keren dat die gebeurtenis voor komt"? Hoe groot is die kans dus?
   2. Hoe groot is de kans dat de volgende persoon die je tegenkomt een kleurenblinde man is? Verklaar waarom het antwoord op deze vraag verschilt van dat op de vorige vraag.

Oefenen

9. In welke van de onderstaande gevallen kun je de kans bepalen door een simulatie met de grafische rekenmachine? Verklaar ook steeds waarom.
   1. De kans op "zes" bij het werpen met twee dobbelstenen.
   2. De kans op "zes" bij het werpen met een dobbelsteen die aan één kant zwaarder is.
   3. De kans op "zes" bij het werpen met een dobbelsteen waar op de zijvlakken 1, 1, 3, 4, 4 en 6 stippen voorkomen.


10. Stel je werpt met twee dobbelstenen in de vorm van een regelmatig viervlak met daarop de getallen 1 tot en met 4. Je let op de som van de getallen die onder komen te liggen.
    Simuleer met behulp van je grafische rekenmachine 20 worpen met twee van die dobbelstenen. Hoe groot is de experimentele kans op 3?


11. Twee spelers A en B spelen een spel: Beiden hebben 2 lucifers waarvan ze er (zonder dat aan elkaar te laten zien) 0, 1 of 2 in de hand nemen, die ze vervolgens dichtgeknepen voor zich op tafel leggen. Tegelijk laten ze elkaar zien hoeveel lucifers ze in de hand hebben. A wint als beide aantallen lucifers precies één verschillen, anders wint B. Ga ervan uit dat het aantal lucifers dat de spelers in de hand nemen uitsluitend van het toeval afhangt.
    1. Hoe zou je dit spel kunnen simuleren met toevalsgetallen?
    2. Geef in een boomdiagram alle mogelijkheden van het spel weer.
    3. Denk je dat dit spel eerlijk is? Met andere woorden hebben A en B een gelijke kans om te winnen?


12. Een fabrikant heeft steekproefsgewijs de levensduur van zijn gloeilampen onderzocht. Je ziet hier de gegevens weergegeven in een tabel. Ga ervan uit, dat de gegevens uit de steekproef maatgevend zijn voor alle lampen van deze frabrikant.
    1. Hoeveel lampen zaten er in de steekproef?
    2. Maak een bijbehorend kanshistogram
    3. Hoe groot is de kans dat een lamp niet meer dan 1250 uur brandt?
    4. Hoe groot is de kans dat een lamp hoogstens 1650 uur mee gaat?
    5. Schat de kans dat de levensduur van een lamp meer dan 100% van het gemiddelde afwijkt.


13. In deze tabel worden de resultaten van het schoolexamens (S.E.) en het centraal examen (C.E.) van een bepaalde school vergeleken. De getallen zijn percentages die zijn ontstaan uit gemiddelden over vele jaren.
    
    
    
    
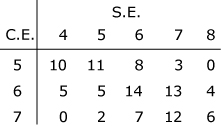
    1. Hoe groot is de kans dat iemand die op het S.E. een 5 scoort, op het C.E. een voldoende haalt?
    2. Hoe groot is de kans dat iemand op het C.E. beter scoort dan op het S.E.?

Toetsen

14. Bij een bepaald spel horen twee viervlaksdobbelstenen waarop de getallen 1 tot en met 4 staan.
    1. Stel je voor dat je er niet zeker van bent dat bij deze dobbelstenen elk vlakje een even grote kans heeft om boven te komen. Hoe kun je jezelf ervan overtuigen dat dit toch het geval is?
    2. Waarom kun je vraag a niet beantwoorden met een simulatie met de grafische rekenmachine?
    3. Neem aan, dat de dobbelsteen eerlijk is. Simuleer nu met behulp van je grafische rekenmachine 80 worpen met deze dobbelsteen. Maak een staafdiagram van de uitkomst.
    4. Hoe groot is de experimentele kans op in totaal 4 ogen?


15. Dit staafdiagram laat de relatieve frequenties zien van de lichaamslengten van 500 soldaten.
    
    
    
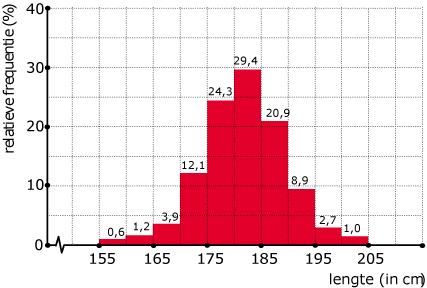
    Een fabrikant ven legertruien gaat ervan uit dat deze relatieve frequenties opgaan voor alle soldaten in Nederland. Hij maakt truien in drie maten:
    • S (small) voor soldaten tot 180`cm`
    • M (medium) voor soldaten van 180`cm` tot 190`cm`
    • L (large) voor soldaten vanaf 190`cm`
    
    
    1. Een soldaat krijgt een nieuwe trui. Hoe groot is de kans dat hij een trui van maat S moet hebben?
    2. Bereken ook voor de andere twee maten de kans dat een trui van die maat nodig is.
    3. De commandant van een legerplaats bestelt 300 truien. Hoeveel van elke maat kan hij het beste kopen?


16. Bij een onderzoek naar linkshandigheid is bij 9000 mensen gevraagd naar hun voorkeurshand. De resultaten vind je in de tabel in percentages. Ga ervan uit, dat deze gegevens maatgevend zijn voor alle Nederlanders.
    
    

    	linkshandig	rechtshandig
    man	11,8	88,2
    vrouw	9,6	90,4

    
    
    1. Je komt op straat een Nederlandse man tegen. Hoe groot is de kans dat hij linkshandig is?
    2. Als je daarna een andere willekeurige Nederlander tegenkomt, hoe groot is dan de kans dat die een linkshandige persoon is?