
Hoeken en afstanden in 3D
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Uitleg
Lees eerst de Uitleg goed door.
- Bestudeer in de Uitleg het berekenen van de hoek tussen en . De aanpak wordt in de uitleg geschetst.
- Bereken de drie zijden van .
- Bereken met behulp van de cosinusregel.
- Bereken nu zelf .
- Bekijk nu hoe in de Uitleg de afstand van tot lijn wordt bepaald.
- Maak zelf de tekening van ruit op ware grootte.
- Geef de gevraagde afstand in je figuur aan.
- Bereken die afstand.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
- Bekijk Voorbeeld 1. Je gaat nu zelf de gevraagde afstand berekenen.
-
Laat zien dat .
-
Teken vierhoek op schaal 1 : 100.
-
Laat vervolgens zien dat .
-
Bereken nu de gevraagde afstand in cm nauwkeurig.
- Bekijk de betonnen zuil uit Voorbeeld 1 nog eens. Er zitten allerlei afstanden in. Soms is het handig om bij het berekenen ervan goniometrie, of zelfs de sinusregel of de cosinusregel te gebruiken.
- Bereken de afstand tussen de punten en .
- Bereken de afstand tussen de punten en .
- Bekijk de betonnen zuil uit Voorbeeld 1 nog eens. Er zitten allerlei hoeken in. Nu is het gebruik van goniometrie onvermijdelijk.
- Bereken .
- Bereken .
- De betonnen zuil heeft nog een bijzondere eigenschap. Als je op hoogte boven het grondvlak een horizontale doorsnede maakt, dan heeft zo’n doorsnede altijd dezelfde omtrek. Toon dit aan.
- In Voorbeeld 2 wordt de hoogte van een opslagruimte berekend.
- Bepaal de vergelijking van de middelloodlijn van .
- Laat met behulp van het antwoord bij a zien, dat de opslagruimte 5 m hoog is.
- Bekijk Voorbeeld 2 nog eens.
- Bij het grootste deel van de vloeroppervlakte hoort een hoogte van 4 meter of meer. Hoe groot is die vloeroppervlakte?
- In punt komen twee cirkels bij elkaar. Welke hoek maken die cirkels in met elkaar?
Verwerken
Lichaam
In de kubus met ribbe 6 cm past een lichaam met hoekpunten en .
is het snijpunt van en , is het snijpunt van en . In de rechter figuur is apart getekend.
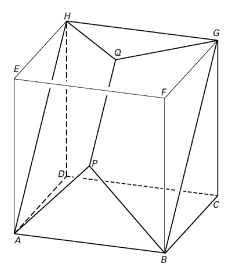
- Bereken de afstand van punt tot punt in één decimaal nauwkeurig.
- Bereken de grootte van in graden nauwkeurig.
Punt is het midden van . In het vlak door de punten en wordt een -assenstelsel aangebracht zo, dat de oorsprong het midden is van , de -as evenwijdig is met en de -as door de punten en gaat.
- De afstand tussen de lijnen en is de lengte van het kortste verbindingslijnstuk tussen beide. Teken dit lijnstuk in het beschreven assenstelsel.
- Bereken de lengte van het in c bedoelde lijnstuk.
- Door en gaat een cirkel . Stel van deze cirkel een vergelijking op.
- Bereken de lengte van het deel van de cirkel tussen de punten en .
Kaasdoos
 In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
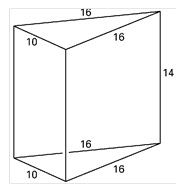
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
De lijnen , , en zijn evenwijdig.
De afmetingen in de figuren zijn gegeven in cm.
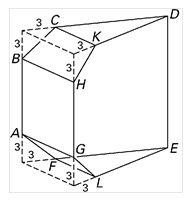
Hieronder is een punt van een Leerdammer kaas getekend, met daarnaast de gehele kaas.
De hoogte van deze kaas is gelijk aan uit de figuur hierboven en de straal is gelijk aan de afstand van tot het vlak .
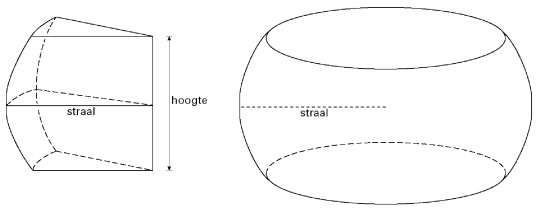
- Bereken de straal van de Leerdammer kaas.
De Leerdammer kaas wordt in een aantal gelijke punten gesneden, zoals in de figuur hierboven. Elke punt wordt verpakt in een kaasdoos. Hoe kleiner de punten, hoe meer kaasdozen er nodig zijn.
-
Bereken het minimale aantal kaasdozen dat nodig is om al deze punten te verpakken.
-
Teken op schaal een dwarsdoorsnede van de kaasdoos door de punten en en het midden van .
Teken daarin ook de dwarsdoorsnede van de kaaspunt en onderzoek of die kaaspunt ook echt in de kaasdoos past.
-
Eén van de zijvlakken van de kaasdoos is vlak . Teken dit vlak op ware grootte en bereken de grootte van de hoeken van dit vlak.
Testen
Keplerster
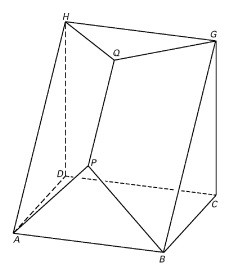
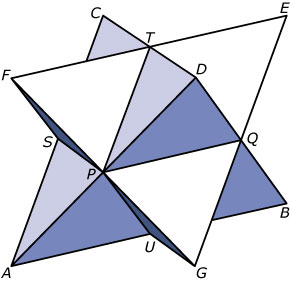 De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken en . Van die viervlakken zijn alle ribben 8 cm.
Viervlak en viervlak doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
en zijn de middens van de ribben van de twee viervlakken.
De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken en . Van die viervlakken zijn alle ribben 8 cm.
Viervlak en viervlak doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
en zijn de middens van de ribben van de twee viervlakken.
-
Bereken de afstand tussen de punten en .
-
Punt is het midden van . Bereken de grootte van .
-
De kleinste bol waar de Keplerster nog precies in past gaat door de punten en . De doorsnede van vlak en die bol is een cirkel .
Bereken de straal van .
-
Bereken ook de lengte van de cirkelboog tussen de punten en .

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Meetkundige berekeningen > Hoeken en afstanden in 3D > Theorie

 In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.


 De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken en . Van die viervlakken zijn alle ribben 8 cm.
Viervlak en viervlak doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
en zijn de middens van de ribben van de twee viervlakken.
De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken en . Van die viervlakken zijn alle ribben 8 cm.
Viervlak en viervlak doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
en zijn de middens van de ribben van de twee viervlakken.